关于
本讲内容将通过一个例子,深入理解决策树模型。在这一讲中,你将学习到:
- 什么是决策树模型?
- 构建决策树模型的算法是怎么实现的?
学习本讲,希望你
- 至少有高中数学水平。
- 如果你需要完成实践部分,需要有基本的 python 知识,你可以通过python快速入门快速了解python如何使用。
本讲所用的数据集还是采用鸢尾花(iris)数据集,你可以从UCI网站上下载https://archive.ics.uci.edu/ml/datasets/Iris。如果已经安装了 scikit-learn,那么可以利用提供的dataset接口直接调用。鸢尾花数据集是著名的统计学家 Fisher 提供的。下面我们采样少量的数据看一看。
| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | target | |
|---|---|---|---|---|---|
| 91 | 6.1 | 3.0 | 4.6 | 1.4 | 1 |
| 77 | 6.7 | 3.0 | 5.0 | 1.7 | 1 |
| 99 | 5.7 | 2.8 | 4.1 | 1.3 | 1 |
| 65 | 6.7 | 3.1 | 4.4 | 1.4 | 1 |
| 14 | 5.8 | 4.0 | 1.2 | 0.2 | 0 |
| 108 | 6.7 | 2.5 | 5.8 | 1.8 | 2 |
| 142 | 5.8 | 2.7 | 5.1 | 1.9 | 2 |
| 127 | 6.1 | 3.0 | 4.9 | 1.8 | 2 |
| 24 | 4.8 | 3.4 | 1.9 | 0.2 | 0 |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | 0 |
该数据集的每一条记录代表一个样本,每一个样本有4个属性变量:
- sepal length (cm) 萼片长度
- sepal width (cm) 萼片宽度
- petal length (cm) 花瓣长度
- petal width (cm) 花瓣宽度
每一个样本有1个目标变量target,target有3个取值,每一种取值的意义如下:
- 0: setosa 山鸢尾
- 1: versicolor 变色鸢尾
- 2: virginica 维吉尼亚鸢尾
这个数据集一共有150个样本,这三种花都有50个样本。上面显示出来的只是随机选取的一部分数据。每一种鸢尾花的图片如下,从左到右分别是 setosa,versicolor,virginica

回顾决策树
在上一讲中,我们简单了解了一下决策树的基本概念。如下图所示,是我们上一讲通过数据分析,设计出来的简单规则模型对应的决策树。决策树首先是一颗树,树由很多节点构成。这些节点分为两类,中间节点(椭圆形)和叶子节点(方形)。中间节点代表一条规则,叶子节点代表模型的决策输出。有多少个叶子结点,就代表有多少条规则。这个决策树实际上代表3条规则,每条规则可以用一个 IF-THEN 条件语句表示:
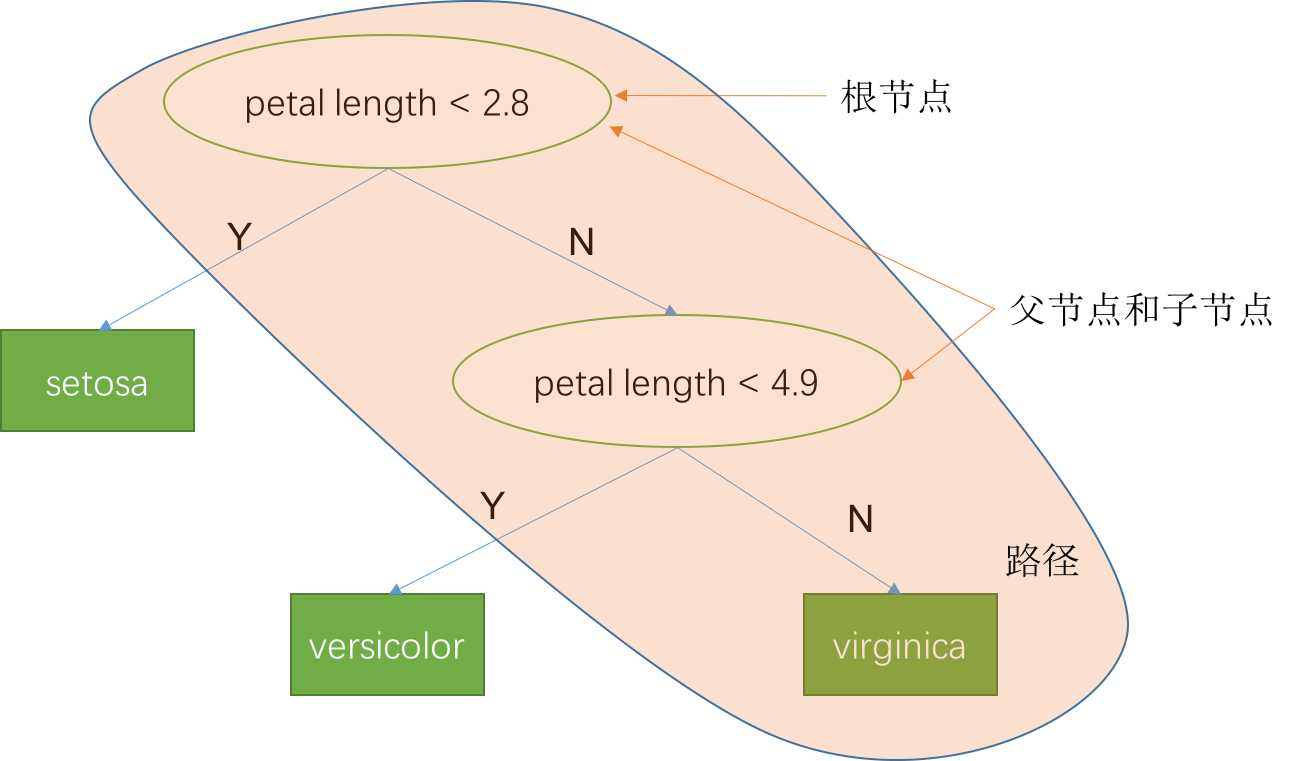
- IF 花瓣长度(petal length) < 2.8, THEN sentosa
- IF 花瓣长度(petal length) >= 2.8 AND 花瓣长度(petal length) < 4.9, THEN versicolor
- IF 花瓣长度(petal length) >= 4.9, THEN virginica
这三个规则,共同定义了一个分段函数!
$$
y =
\begin{cases}
0, \text{petal length} \lt 2.8 \\
1, \text{petal length} \in [2.8, 4.9) \\
2, \text{petal length} \ge 4.9
\end{cases}
$$
对于决策树,我们先定义几个基本概念,便于后面表述:
- 子节点:和节点相连的后继节点,比如节点(petal length < 4.9)是节点(petal length < 2.8)的子节点
- 父节点:当前节点是子节点的父节点。比如节点(petal length < 2.8)是节点(petal length < 4.9)的父节点
- 边:相连相邻两个节点中间的部分叫边,这条边有方向,从父节点指向子节点。
- 中间节点:有子节点的节点,它不直接输出预测结果的节点,对应一个规则。图中椭圆形的节点都是中间节点。
- 叶子节点:没有子节点的节点,直接输出预测结果的节点,对应一个复杂的规则,通常是多个规则的组合。图中方形的节点都是叶子节点。
- 根节点:没有父节点的中间节点。节点(petal length < 2.8)就是上述决策树的根节点。
- 路径:从根节点出发,沿着子节点移动,到达叶子节点时所经历的所有节点序列就是一条路径,图中黄色区域表示出一条路径。路径上边的数量叫做路径长度,实际上也等于中间节点的数目。
- 深度:最大的路径长度,比如上述决策树深度为2.
- 规则:一个可以判定真假的表达式就叫规则,比如花瓣长度(petal length) < 2.8
- 组合规则:多个规则通过且(AND)和或(OR)连接起来的语句叫做组合规则,比如 花瓣长度(petal length) >= 2.8 AND 花瓣长度(petal length) < 4.9
决策树生成算法
在前面一讲,我们通过数据可视化分析,找到了针对花瓣长度(petal length)的3个规则。这些规则的过程能不能够自动化的从已经标注好的数据中找到呢?如果可以的话,那么决策树就可以自动化地生成了,不用再去做数据分析了。答案是肯定的,这就是决策树生成算法。
假设我们对花瓣长度来设计一个规则,一个规则可以看做将它的取值划分成两个区间,我们期望这种划分能够将数据划分成两个更加容易区分类别的集合,这里的关键是找到划分的分裂点的值。划分方法很多,最简单的方法是,选择每一个可能分裂点进行划分,然后找出里面最好的分裂点。
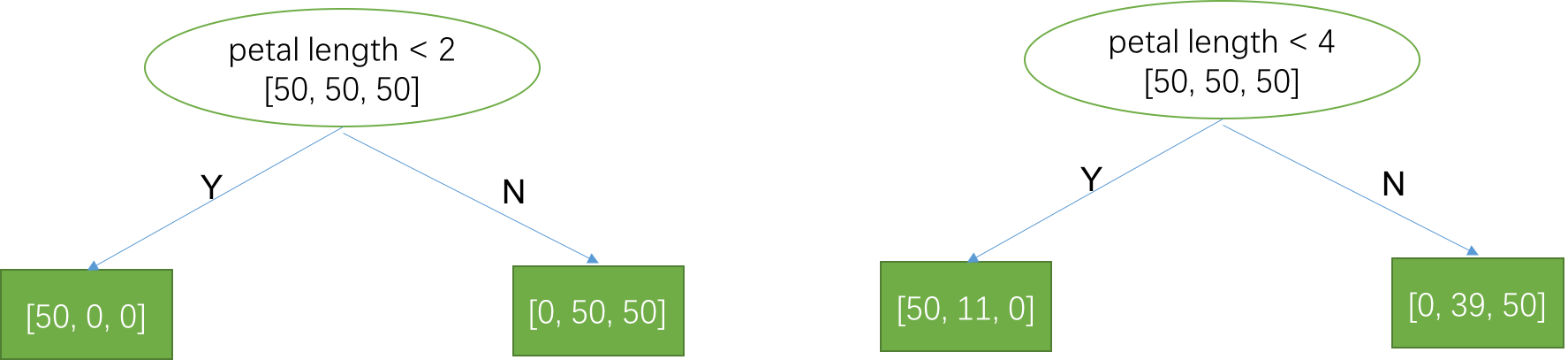
如图所示,是从所有可能的分裂中随机取的两个不同的分裂方式,第一种采用的分裂点是2,在标注类别的训练样本中,三个类别的样本数目都是50个,通过分裂后,落到左边子节点的样本数目分别是[50, 0, 0],即只有第1类的样本,看起来区分性还不错,把第一类完美地识别出来了;落到右边子节点的样本数目分别是[0, 50, 50],第2类和第3类暂时还无法区分,不过不用担心,我们可以沿着右子节点继续分裂下去就可能把这两类也分开来。第二种分裂方式采用的分裂点是4,相比于第一种分裂方式,它把11个第2类样本也放到左边了,看起来区分性没第一种好。那么问题来了,怎么衡量一种分裂方式比另外一种好呢?
信息熵
信息熵可以用来度量一个概率分布$\{p_i, i=1,2,...\}$的不确定度,熵的定义是
$$
H(\{p_i\}) = -\sum_i p_i \log p_i
$$
为什么熵可以度量不确定度呢?我们来看看最简单的一个例子,假设我们抛一枚硬币,如果硬币是均匀的,那么正面和反面出现的概率都是0.5,我们计算一下熵$H = - 0.5\log 0.5 - 0.5\log0.5=\log 2 = 1$(这里为方便记,对数的底取为2)。如果这个硬币不那么均匀,假设正面朝上的概率为0.9,反面朝上的概率为0.1,我们再来计算一下熵 $H = - 0.9\log 0.9 - 0.1\log0.1=0.427$。熵变小了!直观来看是不确定性减小了!因为抛一枚均匀的硬币,确实很难猜测它是正面还是反面,但是如果非常不均匀的硬币,正面朝上的概率是0.9,那么我们有很大的把握猜测它是正面!如果我们把熵H随着正面朝上概率p画一个函数图像,可以看到它在0.5处取最大值,直观理解是均匀的硬币最难猜,熵最大;相反在p=0和1处取最小值,直观理解是只有一面的硬币最好猜,熵最小!
数据量解释
信息熵的另外一个解释是,要描述一个随机事情所需要的最少数据量(比特数)。比特是计算机表达数据量的一个单位,计算机中都是用0和1表示数据,1个这样的0/1单元就是1比特。所以这句话也可以这样理解,如果我要用计算机存储这样一个随机事件的结果,最少要用的数据量。对于一个均匀硬币,我要记录结果是正面还是反面,只要用0表示反面,1表示正面,所以需要1个比特(恰好等于熵)就可以记录结果了。但是如果一枚非常不均匀的硬币,正面朝上的概率为1,那么我们根本不需要记录就可以知道它的结果肯定是正面,也就是需要0个比特,对应的熵为0!如果正面朝上的概率是0.9呢?貌似也需要1个比特才能记录这个事件的结果,如果只记录1个这样的事件,确实如此。如果我们要记录很多个这样的事件时,那么我们可以利用数据压缩工具对结果进行压缩,就好像我们压缩自己电脑上一个普通文件那样。这种压缩有个下界,信息论之父Shanon告诉我们,这个下界就是熵,平均一个事件至少需要H(p)个比特的数据来记录!
一个简单的压缩例子:设想正面朝上的概率是0.9999,记录10000个这样的抛硬币事件,因此记录的数据中大约只有1个为0,其他全部是1。如果我们直接记录原始数据,就需要10000个比特。如果我们只记录这个唯一的0出现的位置,所需要的数据量不会超过32比特(计算机中表示一个整数所需要的比特数)。记录数据量被压缩了近300倍!
平均信息量解释
定义:如果一个事件发生的概率为p,那么这个事件的信息量为 $ - \log p$。
例如,概率为1的事件信息量为0,因为它肯定会发生,所以这件事情发生了没有带来任何信息。如果我告诉你明天太阳会从东方升起,你肯定会认为这是一句废话,没有任何信息量。从概率的角度来解释,因为太阳从东方升起的概率几乎就是1,那么这句话带来的信息量是 $ - \log 1 = 0$比特!相反,如果一件事情发生的概率非常小,几乎等于0,如果它发生了,带来的信息量就非常大,因为$ - \log 0 =\infty $!如果我告诉你一个人把狗咬了,那么你肯定会认为背后有非常多事情没暴露出来,这个消息的信息量非常大,这就是为什么狗咬人不是新闻,人咬狗才是新闻,这可以用信息量解释为新闻的信息量越大,大家越关注。
一个概率分布$\{ p_1, p_2, ..., p_n\}$对应了n个事件,比如投一个六面体骰子,对应6个事件,每个事件的概率是1/6,根据信息量的定义,每个事件的信息量就是 $ \log 6$,这6个事件的平均信息量等于
$$
-\sum_i p_i \log p_i = -\sum \frac{1}{6} \log \frac{1}{6} = \log 6
$$
这正是这个概率分布的熵!
信息增益准则
利用信息熵,我们可以度量每一种分裂方法的好坏。因为熵的意义是不确定度,那么我们计算分裂前后这种不确定度的减少量,不确定度的减少越多,信息量越大,那么分裂后越容易区分每一类,所以分裂方式就越好。基于这个思想,我们定义分裂带来的信息增益
$$
\Delta I = \text{分裂前的不确定度} - \text{分列后的不确定度} \\
= H(P) - [r_1 H(C_1) + r_2 H(C_2)]
$$
P是分裂前数据集中每一类的概率分布,在上述的第一种分裂中,分裂前三个类别的样本都是50,所以每一类都是1/3的概率,所以$H(P) = \log 3 = 1.098$。C1是分裂后分到左子树的数据中每一类的概率分布,在分裂规则petal length<2下,分到左子树的样本有50个,且全部是第一类,所以三个类别的概率分布是$\{1, 0, 0 \}$,$H(C_1) = 1\log1 + 0\log 0 + 0\log0 = 0(0 \log 0 = 0)$。$r_1$是左子树的样本占分裂前的比例,$r_1 = 50/150=1/3$。同样,分到右子树的样本分别是[0, 50, 50],所以$H(C_2) = 2/3\log 2 = 0.462, r_2=2/3$。因为分裂后有两个样本集合,所以需要把这两个集合的不确定度平均一下,平均的方式是按照样本数目的加权平均。根据信息增益公式,可以得到 $\Delta I = 1.098 - [1/3 * \log 0 + 0.462*2/3] = 0.79$。
类似的,我们可以计算第二种分裂方式的信息增益,按照上述逻辑计算结果为$\Delta I = 0.500$。这表明第二种分裂方式的信息增益没有第一种好,直观解释就是第二种分裂方式带来的信息量没有第一种多,这与我们直观感受一致。
信息量解释:不确定度的减少就是信息量,比如在抛一枚均匀的硬币时,知道结果之前,不确定度为1比特,知道结果后,不确定度为0,不确定度减少量是1比特,也就是这个结果带来的信息量。信息增益是分裂前后不确定度的减少量,所以实际上就是分裂带来的信息量。
利用信息增益准则,我们可以设计出最佳分裂点算法,对于某个特征,在所有可能的分裂点计算分裂的信息增益,信息增益最大的分裂点就是最佳的分裂点!可能的分裂点可以将该特征所有取值按照顺序排列$\{z_1, z_2, .., z_k, ...,z_n\}$,任何两个值的平均值$ (z _ i + z _ {i+1})/2$都可以作为候选分裂点。
最后一个问题,这么多个特征我们应该先选择那个特征分裂呢?只有先选择好分裂那个特征,才能利用上面的步骤选出最佳分裂点。方法也很简单,我们对每一个特征$x_i$都计算它的最佳分裂点$t_i$和最大信息增益$\Delta I_i$,然后将信息增益最大的特征$i ^ * $作为当前最佳分裂特征即可。因此,决策树生成算法中每一次进行分裂的过程可以归纳为如下步骤:
- 计算分裂前的信息熵H(P)
- 对每一个特征的每一个可能的分裂点,计算分裂后的信息增益,找到最大增益的特征$x_i$和分裂点$t_i$
- 得到分裂规则 $x_i < t_i$ 和最大信息增益
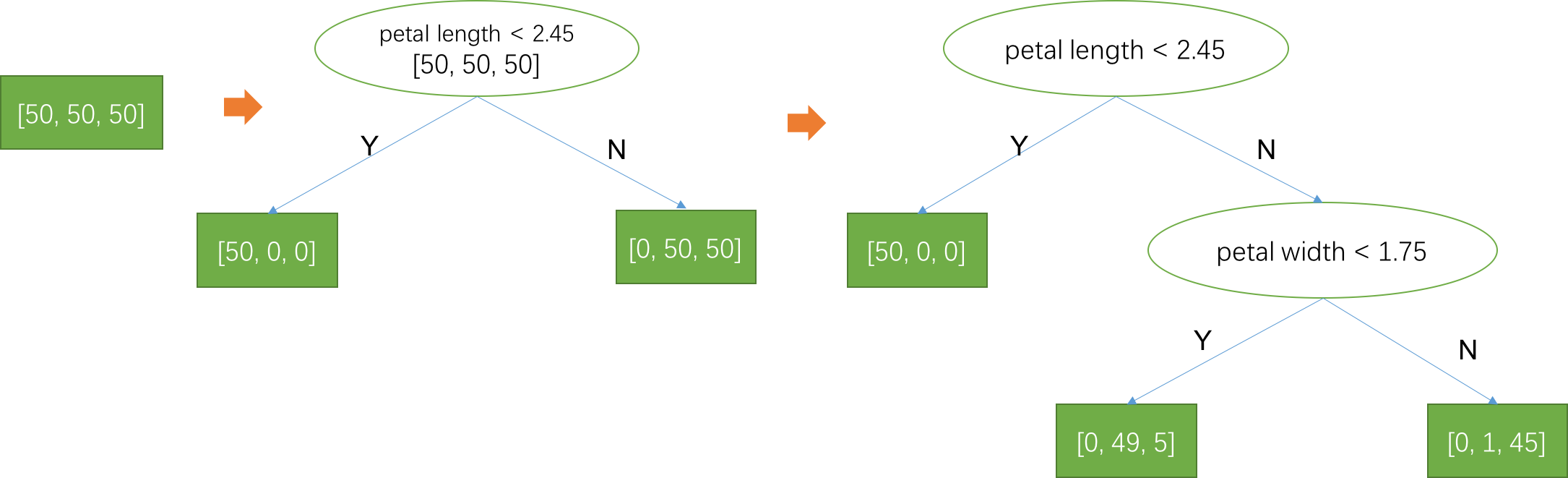
利用上述分裂算法,可以很容易得到决策树生成算法,从训练集合开始,运行上述分裂算法找到一个最佳分裂规则,将集合分裂成两个集合。如下图所示,一开始训练集中3类数据都是50个样本,分裂算法找到的当前最佳分裂规则是(petal length<2.45)。这个规则将训练集分为两个规则B和C,集合B中有50个样本,全是第一类,集合C中有100个样本,其中50个是第2类,50个是第3类。接着,对集合B和C继续分别运行分裂算法,相当于将B看做新的训练集合,生成左子树;将C看做新的训练集合,生成右子树。将这个步骤不断迭代下去,直到达到某个准则为止。例如在第一次分裂后,分到左边的B集合里面只有一类,已经没有不确定性了,没有必要继续分裂,这就是第一个停止准则:如果集合只有一类样本,那么就停止分裂。而分到右边的C集合没有满足停止准则,所以把C集合看做一个新的训练集,运行分裂算法找到最佳分裂规则为(petal width<1.75),C集合继续分裂成两个子集,这两个子集满足第2个停止准则:如果决策树的深度达到某个阈值,那么就停止分裂。这里我们要求深度不能超过2,所以这两个子集就停止分裂了。除了这两个准则外,还有一些准则,比如每个叶子节点的样本数目不能少于10个,因为叶子节点上样本数目太少,那么满足这条组合规则的样本太少了,这说明这条规则没有代表性。叶子节点上类别最多的类别,作为在输入满足这个叶子节点对应规则时,模型的输出结果。例如,最左边的叶子节点全是第一类,因此这个叶子节点预测的结果是第一类,也就是说如果输入满足规则(petal length<2.45),那么模型的预测结果就是第一类。如果所有的分裂都达到停止准则了,那么一棵决策树就生成好了,然后就可以用这个决策树模型对未知数据进行预测啦!
决策树生成算法步骤总结如下:
- 初始化A=训练集
- 如果集合A的数据量小于一个阈值或者只有一类样本,停止分裂。否则进入第3步。
- 对集合A,依次选取第i个特征进行分裂,利用分裂算法计算该特征的信息增益和分裂规则,选取信息增益最大的特征作为当前分裂特征,对应的分裂规则作为当前的分裂规则。
- 利用第3步生成的分裂规则,将集合A划分为两个子集B和C。对这两个子集继续应用生成算法生成左子树和右子树。
生成算法的每一个分裂步骤可以看做对所有的可能的分裂规则进行穷举,在鸢尾花识别这个任务中,特征有4个,假设在一开始分裂的时候,每个特征有100个可能的分裂点,那么就有400个可能的分裂方式,生成算法就是穷举这400个分裂规则,利用信息增益准则来评估这些规则,找出最佳规则作为决策树的规则!这个方法看起来很笨,不像我们可以观察一下分布图就知道最佳分裂点了,但是这是目前的计算机最有效的处理方式了。
决策树的几何解释
在前面,我们一直把决策树看做很多规则构成的分段函数。接下来,我将介绍决策树的一个直观的几何解释。如果我们用决策树分类的特征做为坐标轴,例如我们以花瓣长度(petal length)为横轴,花瓣宽度(petal width)为纵轴。我们将数据绘制于这样一个二维平面中,如下图所示,每一个类别的数据都用不同的颜色表示出来。上述的决策树的第一个规则是(petal length<2.45),这相当于用图中垂直于横轴的绿色虚线将这个平面分割为左右两半,左边对应于(petal length<2.45),而右边对应于(petal length>2.45);第二个基本规则是(petal width<1.75),因为这个规则是在(petal length>2.45)条件下应用的,所以相当于用图中平行于横轴的红色虚线将前面分隔开的右半空间继续分割为两部分,上边对应于组合规则(petal length>2.45 && petal width>1.75),下边对应于组合规则(petal length>2.45 && petal width<1.75)。经过这两个划分,分别形成3个区域,每个区域对应一个组合规则,同时也对应决策树的一个叶子节点!从几何上,可以直观地看出,这个决策树确实将这三类数据区分开了!
因此,从几何上来看,决策树可以看做对特征构成的空间进行划分,划分的边界对应于特征的分裂点,划分后形成的每一个区域与决策树的叶子节点一一对应!
决策树的可解释性
前面我们说到,机器学习就是在寻找一个可以描述数据规律的函数,复杂的函数基本上是个黑盒子,很难被人理解。决策树是其中为数不多可解释性高的模型,因为它就是很多规则嘛!当一个决策树模型训练好了,我们可以将决策树模型画出来。在预测时,我们根据样本的特征可以知道这个样本是被决策树的哪条规则命中,从而得到预测结果的。例如,如果一个样本满足规则(petal length<2.45),那么模型的预测结果是山鸢尾。如果有人问你模型怎么判断的,那么你可以很肯定的告诉他,模型是根据这朵花的花瓣长度小于2.45厘米来判断的。这个好用的性质并不是所有模型都具备,例如后面要讲到的神经网络,可解释性就很低。
思考与实践
- 证明对于任何一种分裂方式,信息增益非负。
- 实现上述基于信息增益的决策树生成算法,启动代码已提供
from sklearn.datasets import load_iris import numpy as np from scipy import stats def H(arr): """计算熵的函数""" n = sum(arr) arr = [1.0*i/n for i in arr] return sum([- p * np.log(p) for p in arr if p >0]) def InformactionInc(x, y, split): """计算利用split分裂特征x时,信息增益 x : np.array 特征数组, size= (样本数, ) y : np.array 类别, size=(样本数, ) split : double 候选分裂点的值 return : 信息增益 """ delta = 0 # Your Code # end return delta def FindSpliter(X, y): """寻找最佳分裂特征和分裂点算法 X : np.array 特征,size = (样本数, 特征数) y : np.array 类别,size = (样本数, ) return (分裂特征索引 i, 分裂点的值 t) """ n_samples , n_features = X.shape max_infor_inc = 0 best_feature = 0 best_split_value = None # Your Code # end return best_feature, best_split_value def TreeGenerate(X, y, depth=0, max_depth=3): """决策树生成算法,返回一棵树 """ # 满足不分裂准则 if X.shape[0] < 10 or np.unique(y).shape[0] == 1 or depth >= max_depth: node = {'prediction' : stats.mode(y)[0][0]} return node # 继续分裂 best_feature, best_split_value = FindSpliter(X, y) mask = X[:, best_feature] < best_split_value node = { 'left' : TreeGenerate(X[mask, :], y[mask], depth+1), 'right' : TreeGenerate(X[~mask, :], y[~mask], depth+1) } return node def TreePredict(X, T): """实现决策树预测算法""" pass iris = load_iris() T = TreeGenerate(iris.data, iris.target) print(T) print( 'ACC: {}'.format(np.mean(TreePredict(X, T) == iris.target)) )

