关于

强化学习近年大火，最早是因为AlphaGo使用强化学习打败人类围棋冠军引发的。在那之后，强化学习在工业场景应用越来越多，原来很多做搜索、推荐、广告等一直在用监督学习的业务，也开始使用强化学习来优化用户体验和平台收益了。强化学习实际上很早就提出了，事实上，强化学习来源于控制论。控制论之父叫做维纳，学过信号处理的可能知道他，维纳滤波就是用他的名字命名的。控制论最早源于航天，人们要控制火箭发射装置，将火箭发射到地球之外；控制论还源于机器人控制，人们需要用算法对机器人的行为进行控制。所以，很多讲强化学习的文献也会说强化学习是在优化控制策略。

在这篇文章中，您将学习到

1. 强化学习是什么？可以干什么？
2. 马尔科夫决策过程(MDP)的重要概念
3. 哈密顿-雅克比-贝尔曼(HJB)方程
4. 已知环境下HJB方程的求解算法：值迭代和策略迭代

我期望您至少有：

1. 高中数学水平且年满18岁，部分内容需要你了解监督学习，你可以通过本教程前面的章节进行学习。
2. 如果你需要完成实践部分，需要有基本的 python 知识，你可以通过python快速入门快速了解python如何使用。

马尔科夫决策过程

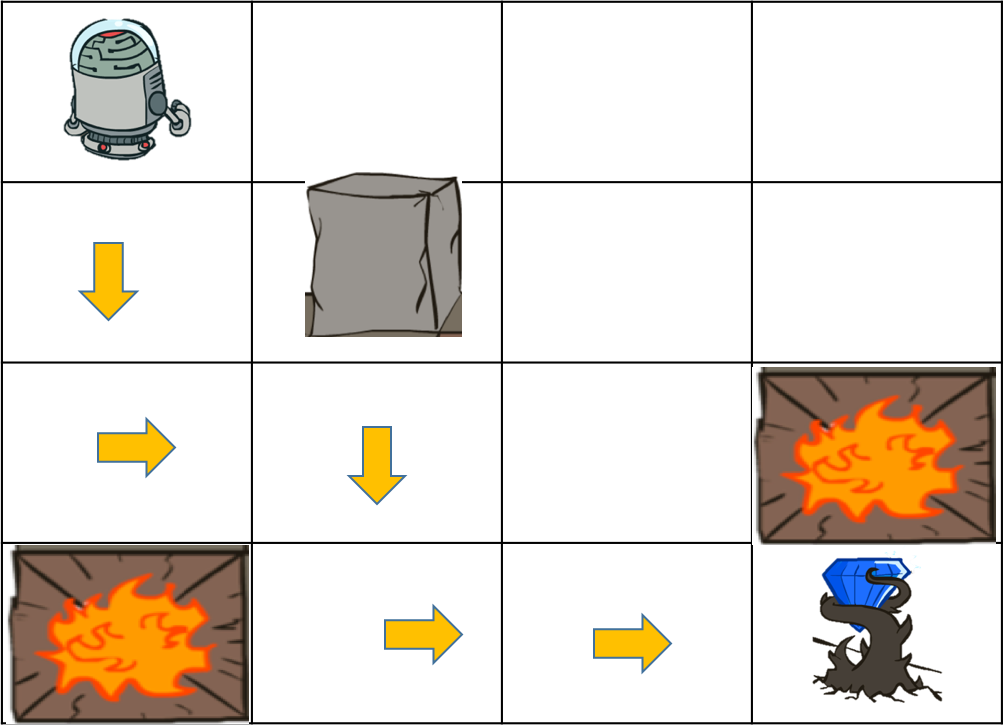
考虑下面的迷宫游戏问题，你控制一个机器人在一个二维迷宫中运动，迷宫中有正常的陆地、火坑、石柱、钻石。你可以控制机器人上下左右运动，机器人不能走到迷宫外面，一次最多只能运动一步，如果不小心掉到火坑中，游戏结束，如果找到了钻石，那么可以得到奖励，并且游戏结束！由于你的控制是通过语音指令控制，机器人有一定概率会判断出错。比如你说让机器人往左走，机器人有一定概率会往右走，所以机器人的移动和你的指令之间并不是完美匹配的。你的目标是通过设计策略，让机器人尽快地找到钻石，获得奖励。

上述问题有几个关键要素：

1. 状态：机器人所处的位置是有限的，我们把每一个位置称作一个状态，那么一共有15个状态（有一个是石柱，机器人无法到达这个位置）。其中两个是火坑，一个是钻石，由于机器人进入这些状态就会结束游戏，我们称为终态。我们用S来表示状态，那么S可以有15个取值，我们一次用数字标识这15个状态，那么$S \in \{1,2,...,15 \} $。
2. 动作：在每个不是终态的状态下，我们都有4个控制动作，上、下、左、右，我们也可以将这些动作依次编号为1到4，用A表示动作，那么$A \in \{1,2,3,4 \}$。
3. 转移概率：因为我们是通过声音控制机器人的，所以机器人可能听错，可以认为是语音识别技术尚不成熟的原因。那么在某个状态S，采取动作A之后，机器人到达的状态并不是完全确定的。例如当机器人在左上角时，采取“右”这个动作时，机器人也有一定概率会向下移动，进入状态5（假设状态按照从左到右顺序编号）。为了描述机器人的这种不确定运动，可以用一个转移概率来表示。我们用P(S'|S, A)表示在状态S下，采取动作A的条件下，机器人进入状态S'的概率。例如在刚才这个例子中，P(S'=5|S=1, A=右)就表示在状态1（也就是左上角），采取动作右的条件下，进入状态5（也就是第二行第一个状态）的概率。所以，这个转移概率描述的是机器人所处状态在我们的控制下变化的规律。
4. 回报：在机器人每一步运动到下一个状态时，环境会给我们一个奖励或者惩罚，例如如果进入火坑游戏就会结束，而拿到钻石就会得到奖励，这种奖励或者惩罚我们用数量来量化。我们可以用正数表示奖励，负数表示惩罚，这就是回报。一般情况下，回报可能跟状态和动作都有关系，所以我们用一个函数来表示 R(S, A, S')，它表示在在状态S下采取动作A到达状态S'时，获得的回报。注意，一般情况下，回报是在每一个动作执行后跳转到新的状态就会收到的，而不是只有最后到达终点时才有。在这个例子中，只有最终的那一步才有回报，可以认为其他的每一步的回报为0。你也可以给其他的步骤给一个负的回报，负的回报可以解释为每一步付出的成本，例如时间成本、机器人的能量消耗等等。
5. 马尔科夫性：描述环境的转移概率只跟当前状态和动作有关，而与之前经过的状态和动作无关，这种性质叫做马尔科夫性（因为是一个叫马尔科夫的人最早提出来的）。在这个例子中，机器人在我们的控制下要进入的状态的概率只与当前的状态和我们的控制动作有关，而与在这之前机器人经历过的状态无关。例如，当机器人处于状态1时，那么接下来，采取动作"右"后，状态变到2还是5的概率与机器人到达状态1之间的所有事情都无关！这种无关，并不是说最终获得的回报与之前的状态无关，而是说当前这一步的转移概率与之前的状态无关！并不是所有的决策事情都有马尔科夫性的，比如股票，今天涨跌不但与昨天有关，还与之前的多天有关。如果我们用$S_t, A_t$分别代表t时刻的状态和采用的动作，那么马尔科夫性可以表示为

$$
P(S_{t+1}|S_t, A_t, S_{t-1}, A_{t-1}, ...,S_1, A_1) = P(S_{t+1}|S_t, A_t)
$$

这个公式的左边是在前面一系列的状态和动作的条件下，下一步转移到状态$S_{t+1}$的概率，右边是在当前状态$S_t$下，采取动作$A_t$后，转移到状态$S_{t+1}$的概率，而不管更前面的状态和动作是什么。这两者相等，就是说转移概率只跟当前状态和动作有关，而与之前经过的状态和动作无关，即上面说的马尔科夫性。

马尔科夫性也叫无记忆性，想象一个得了一种奇怪失忆症的病人，他每天醒来时，就会将以前发生的事情全部忘记。马尔科夫性就像一个不记事的系统，这种系统只是对实际问题的一种理想近似，可以简化数学模型。

上述问题可以抽象为上述4个要素和1个性质的普遍问题，因为环境具有马尔科夫性，我们需要做出决策对机器人进行控制，所以叫做马尔科夫决策过程(Markov decision process，MDP)。对于这类问题，我们在每一步决定要采取那个动作的策略可以用一个策略函数来表示$\pi(A | S)$，这个函数的意义是在状态S下，采用动作A的概率。对于确定性的策略可以看做它的一个特例，即只有一个动作的概率为1其他为0.例如，我们可以定义一个确定性策略如下：如果右边能走，就往“右”，如果右边不能走，就往“下”。用数学公式表示为

$$
\pi(S) = \begin{cases}
\text{右}, S \in \{1,2,3,6,8,9,10,12,13,14 \} \\
\text{下}, S \in \{4,7,11 \}
\end{cases}
$$

MDP问题的目标是找到这样一个策略，在这个策略下，总的期望折扣回报最大化！总期望折扣回报定义如下

$$
R = E \sum_{t=1}^{\infty} \gamma^{t-1} R(S_t, A_t, S' _ t), \gamma \in (0, 1]
$$

也就是在这个策略下，将所有获得的回报打个折之后全部加起来。越往后的折扣越大，这是因为我们更关心离当前时间更近的回报。这个回报越大，说明这个策略越好，使得回报最大的策略就是最优策略。因为环境有一定的随机性，在这个策略下实际的回报是随机的，所以我们对回报求期望，得到期望折扣回报。

以上述迷宫为例，我们假定游戏结束后回报全部为0，状态也不改变了。那么上述求和只到游戏结束，假设折扣因子为1，跳到火坑的回报为-1，找到钻石的回报为+1，其他情况回报为0。那么一个找到钻石的策略的总回报就是1！而跳到火坑的策略的总回报为-1. 由于环境的随机性，实际的策略下这两种情况都有可能，所以一般期望回报在-1到1之间。一个策略越好，那么期望回报会更接近1，期望回报最大的策略就是我们要寻找的最优策略。

MDP的例子

设想你在跟朋友玩斗地主（一种流行的扑克牌游戏，你可以类比于所有你熟悉的牌类游戏），影响你每一步出牌的信息包括每个人手中的剩下的牌的张数，每一个人已经出过的牌，还有你自己目前手中的牌，这些信息构成了一个状态(S)。你的出牌动作可以从所有可能的出牌方式中选择一个，比如3带1或者一对A都是一个动作(A)。可以想象，状态数目和动作数目都非常大，但是不用担心，计算机很容易处理大量的状态和动作的任务，但是前提是你要把MDP中的所有元素定义清楚。你每次出牌之后，到你下一轮出牌时，完成了一个状态转移，转移到的状态就是下一轮出牌时，每个人剩下的牌的张数，每个人已经出过的牌，还有你自己手中当时的牌。由于你无法决定其他人的出牌，所以对你的某一个出牌动作，转移到的状态也是不确定的，存在着转移概率(P)。但是这个转移概率在当前的状态和你的动作给定的情况下，而与之前的状态和动作无关，因为根据我们对状态的定义，它已经包含了这些信息，所以不用管之前的状态了，这表明这个任务满足马尔科夫性。我们的目标是要最终赢得这一局牌，可以将赢了的回报(R)定义为+1，而将输了的回报定义为-1，其他每一步的回报都是0。那么玩斗地主游戏的过程具有上述4个要素和1个性质，因此在计算机设计斗地主算法时，就可以用马尔科夫决策过程来描述！

设想你是一只AlphaGo，正在和人类下围棋，影响你每一步落子的信息就是当前的棋局状态(S)，而你每一个落子动作(A)都是从所有可能的落子位置中选择的一个。从你当前落子到下一步落子时，状态发生了转移，又有你不知道对手会下哪一步，所以存在状态转移概率(P)。这个转移概率只与当前的棋局状态和你的落子动作有关，所以具有马尔科夫性。我们的目标是最终要赢得这一局牌，每一局牌结束时都会有一个回报(R)。因此，AlphaGo下围棋的过程具有上述4个要素和1个性质，因此可以用马尔科夫决策过程(MDP)来描述。事实上，在Google最新版的AlphaGo程序中，正是通过MDP来对下围棋这个过程进行建模的。

设想你是一个航天控制系统设计工程师，你想让火箭按照预期将卫星发射到预定轨道当中。火箭在每一个时刻上所处的位置和速度共同构成了一个状态(S)，而你设计的控制算法每个时刻所给出的推动策略(加速喷火还是减速喷火等等)就是一个动作(A)。这个问题中，状态是连续的，动作既可以是有限的也可以是连续的。每一个动作执行后，由于受到环境的干扰（阻力，控制误差等等因素），下一个时刻火箭的状态存在着一个转移概率(P)。这个转移概率在当前时刻的状态和动作给定的情况下与之前火箭的状态和控制动作无关，这表明任务满足马尔科夫性。我们的目标是用最少的能量消耗将火箭发射到预定轨道，每一步的回报(R)是负的，因为每一步消耗了燃料，总的回报就是负的消耗总能量。最大化总回报就是最小化能量消耗，因此上述火箭控制系统可以用马尔科夫决策过程来描述。

这样的例子还有很多，可以看到，很多实际的决策和控制问题，都可以看做马尔科夫决策过程(MDP)，因此MDP应用非常广泛，从斗地主到火箭发射，几乎无所不在。

确定性环境

假设我们可以直接控制上述机器人，那么在某个状态S，采用动作A后，机器人到达的状态S'就是确定的，也就是转移概率P(S'|S, A)只可能取0和1两个值！这种情况下，我们说环境是确定的，这就是我们正常的迷宫游戏。

在环境是确定的，没有随机干扰情况下，我们很容易看出，下图所示的一个策略就是最佳策略，箭头所指的方向就是在当前状态下，应该采取的动作。因为在这个路劲上，除了最终的状态，其他状态回报都是0，只有到达最终状态的时候有一个+1的回报，所以这个策略的总回报等于1。不难想象，这个策略并不是唯一最优的策略，例如在这条路径上往回走一段路程之后再往前走，总回报还是等于1，因为中间所有的状态的回报都是0。

如果我们想要得到最短的路径，该怎么办呢？方法很简单，我们可以让除了到达终态的步骤外，其他每一步的回报为-0.1即可！虽然这样一来，但是只有最短路径的策略可以获得最大总回报，容易计算出最大总回报等于0.5。你可以把每一步回报为负数看做成本，例如你控制的机器要消耗电，不必要的步骤就是在浪费你的时间，增加时间成本。在最短路径找到钻石实际上是在说用最少的成本得到最大的回报！

另外一个方法是让折扣因子小于1，比如取0.9，每一步的回报还保持为0不变，那么路径越长，最后得到的那个回报就会被衰减得更多，只有最短路径才能得到最大回报，此时最大回报为

$$
R = 0 + 0 + 0 + 0 + 0 + 0.9^6 = 0.531
$$

折扣因子实际上是再将未来的回报折现到现在，想想给你的回报是很多年后的1万块钱，那么同样是一万块钱，年限不同决定了其价值也不相同（想想一下2000年的1万元和2010年的1万元的价值明显是不一样的，因为货币会贬值）。为了统一衡量这些不同年限的回报，可以将他们折现到当下，看他们在现在值多少钱。折扣因子就是折现率，它将未来的回报折现到现在便于统一比较！

因此，从这个例子来看，在对实际问题建模的时候，合理设计回报也是一个很重要的事情。

随机策略

这个简单的例子我们很容易利用上帝视角，发现最佳的策略$\pi^ * $使得总回报最大，就是上图中的最短路径。但是，设想一下，我们是图中那个机器人，身在此山中，云深不知处，无法开上帝视角，不知道上下左右分别是什么坑，只知道自己所处的位置是否有坑，因此就不知道采取某个动作之后会得到什么，除非我们去尝试一下。在这种情况下，我们该采用什么策略呢？没有太好的办法，只有采用随机策略去尝试。

所谓随机策略就是每个状态下，选择上下左右四个动作的概率都不为0，比如在对环境一无所知的情况下，可以将每个方向的概率都设为一样。当你经过尝试或者通过其他途径获得了一些关于环境的信息，你也可以让某个方向上的概率更大一些，例如有人告诉我，钻石就在最右下角，那么我们可以不用采用那么随机的策略，让向右和向下这两个动作的概率更大一些。这表明，我们知道的信息越多，可以采用的策略就越不用那么随机。如果我们对环境十分清楚，例如我们知道每一个状态下每一个动作执行后会转移到哪个状态(即知道转移概率P)，并且知道哪些状态是坑，哪些是钻石(也即是知道了回报函数R)，也就是开了上帝视角，知道环境的转移概率和环境的回报函数，那么我们原则上可以计算出这个最佳的策略。那么问题来了，在环境的转移概率和回报函数已知的情况下，怎么求解最佳策略呢？

哈密顿-雅克比-贝尔曼(HJB)方程

在回答上述问题之前，我们先来介绍一个方程，叫做哈密顿-雅克比-贝尔曼(HJB)方程，很明显这个方程跟三个人有关，这三个人都是很有名的数学家，哈密顿还是个数学物理学家，是哈密顿力学的创始人。这个方程刻画了最优策略要满足的充分必要条件，一旦这个方程求解出来了，那么最优策略也就知道了。在介绍这个方程之前，我们先来介绍两个在强化学习中非常重要的概念，状态值函数和动作值函数，熟悉这两个概念对以后的学习十分重要，我们会不断的碰到这两个概念。

状态值函数

当我们知道环境的状态转移概率时，那么很直接的想法是查看四周，找到最好的一个状态，然后选择可以到达这个最好的状态的动作。例如在状态8的时候，周围的状态只有3个，12是火坑，5和9是普通的状态，显然12这个状态不能跳，状态9看起来比5好，因为它离钻石更近一些。但是在复杂的问题中，我们很难用这样一个简单的法则来表达状态是好还是坏，因为在复杂的问题中，随机性可能比较大，最短距离可能并不是最佳的。例如状态6比2到达钻石的距离短，但是如果状态6到达10的转移概率很低很低，那么状态2可能比6更好。这表明最短路径并不是一个很好的评估一个状态指标。那么如何精确评估一个状态好还是坏呢？答案就是状态值函数。

定义：状态值函数V(S)是从状态S出发，所能获得的最大期望回报！

$$
V(S) = \max E \left[ \sum_{t=1}^{\infty} \gamma^{t-1} R(S_t, A_t, S' _ t) | S_1=S \right]
$$

我们假设环境是确定性的，没有随机性，这样可以省去求期望的步骤，便于理解状态值函数。对于终止状态，我们定义它们的状态值函数值恒等于0。假设折扣因子等于1，每一步跳转的回报函数都为-0.1，仍然假定环境是确定的。我们来看一下从状态13出发，可能到达的状态有3个，分别是12、9、14，我们来计算一下这三个状态的状态值函数。因为12是火坑，是终止状态，所以V(12)=0。对于状态9，最快可以通过3步到达钻石，获得的总回报是V(9)=-0.1-0.1+1=0.8。而状态14最快一步就能到达钻石，所以总回报就是这一步的回报V(14)=1.很明显，V(14)>V(9)>V(12)，所以这3个状态中，状态14最好，这跟我们的直觉一致。这表明状态值函数可以评估两个不同状态的好坏。

状态值函数的求最大值操作表明采用的是最优策略$\pi^ * $下的总折扣回报，对于某个具体的策略$\pi$，还可以定义策略值函数为：从状态S出发，采用策略$\pi$选择动作，所能获得的期望回报！

$$
V^{\pi}(S) = E \left[ \sum_{t=1}^{\infty} \gamma^{t-1} R(S_t, A_t, S' _ t) | S_1=S, A_t \sim \pi \right]
$$

$V^{\pi}(S)$和$V(S)$都是从状态S出发获得的最大期望回报，不同的是$V^{\pi}(S)$要求后面采取的策略是给定的策略$\pi$，而$V(S)$要求的是最好的策略。假设从状态S=13出发，策略$\pi_1$是一直往上走，如果上面不能走就往右走（下图绿色箭头）。策略$\pi_2$是一直往右走，右边走不了就往下走(下图黄色箭头)。在策略1下，机器人会跳到火坑里面（这里还是认为是确定性环境，每一步回报为-0.1，火坑回报-1，钻石回报+1），所以$V^{\pi_1}(13)=-1.2$，而在策略2下，机器人将找到钻石，所以$V^{\pi_2}(13)=0.9$。显然在状态13下，策略2更好，对应的策略值函数也越大。因此，策略值函数$V^{\pi}(S)$可以用来评估一个策略好不好。

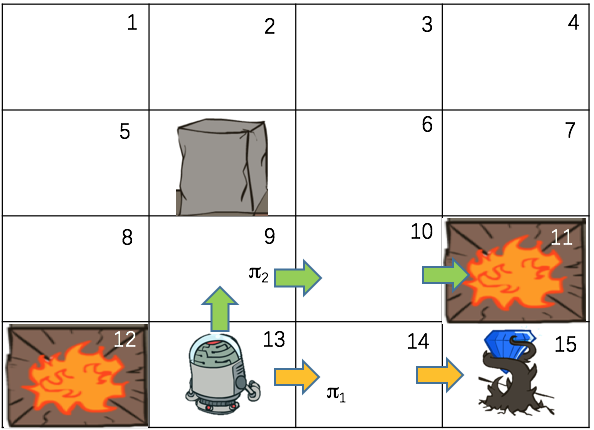
状态值函数$V(S)$与策略值函数$V^{\pi}(S)$不同的是，前者采用的是最佳策略，而后者采用的是具体的某个策略$\pi$。两者的关系是，$V(S)$是采用最佳策略$\pi ^ * $下的策略值函数，即$V(S) = V^{\pi ^ * }(S)$。

动作值函数

前面的状态值函数可以用来评估一个状态好不好，那么在一个给定的状态下，怎么评估某个动作好不好呢？答案是动作值函数！

定义：动作值函数Q(S, A)是从状态S出发，采用动作A后，所能获得的最大期望回报！动作值函数也称Q函数。

$$
Q(S, A) = \max E \left[ \sum_{t=1}^{\infty} \gamma^{t-1} R(S_t, A_t, S' _ t) | S_1=S, A_1=A \right]
$$

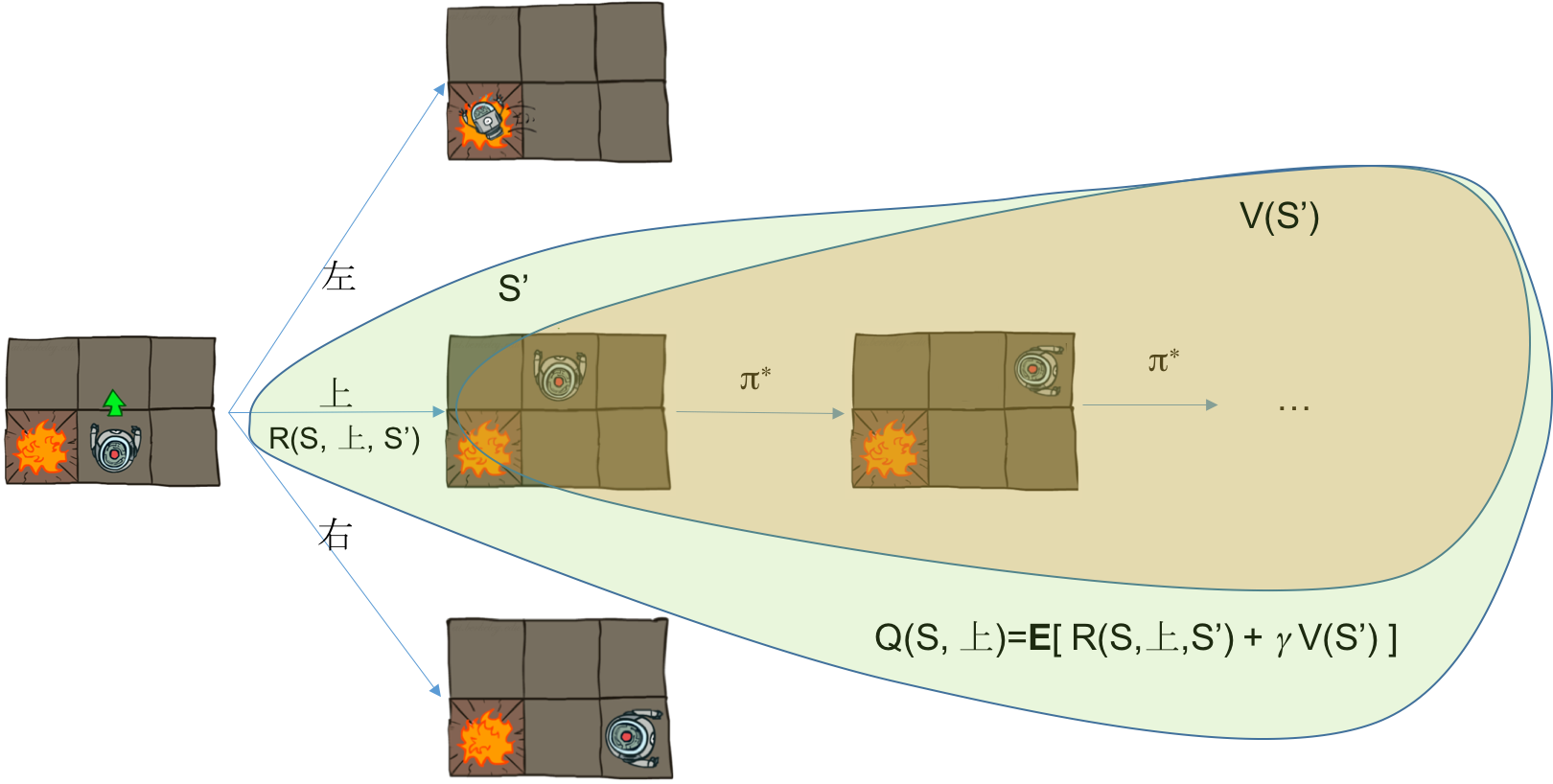
求和包括两部分，第一部分是第一步采用动作A后调到状态S'所获得的单步回报$R(S, A, S')$，第二部分是从S'开始采用最优策略所获得的最大回报，这一部分可以用状态S'的值函数表示$V(S')$。所以总回报为$R(S, A, S') + \gamma V(S')$。考虑环境的随机性后，需要对所有的可能状态S'求期望，于是有如下关系

$$
Q(S, A) = \sum_{s'} P(s'| S, A)[ R(S, A, s') + \gamma V(s') ]
$$

以确定性环境为例（如上图所示），设单步回报为-0.1，在初始状态S时，可以有3个动作，分别是上、左、右，当第一步采用动作上后，所获得的回报包括两部分，第一部分是执行动作上后调到状态S'的回报R(S,上,S')，第二部分是从S'开始采用最优策略所获得的回报，这正是状态值函数的定义，所以这部分回报是V(S')。综上可得动作值函数$Q(S,上) = R(S,上,S') + \gamma V(S')$。

根据值函数的定义，对初始状态S，其值函数V(S)是之后每一步都采用最优策略带来的总回报期望值。而动作值函数Q(S, A)要求第一步必须采用动作A，从第二步开始才采用最优策略，如果第一步采用的动作A就是最优策略的动作，那么动作值函数就等于状态值函数！也就是

$$
V(S) = \max_a Q(S, a)
$$

并且可以得到最优动作$A^ * = \arg\max_a Q(S, a)$。

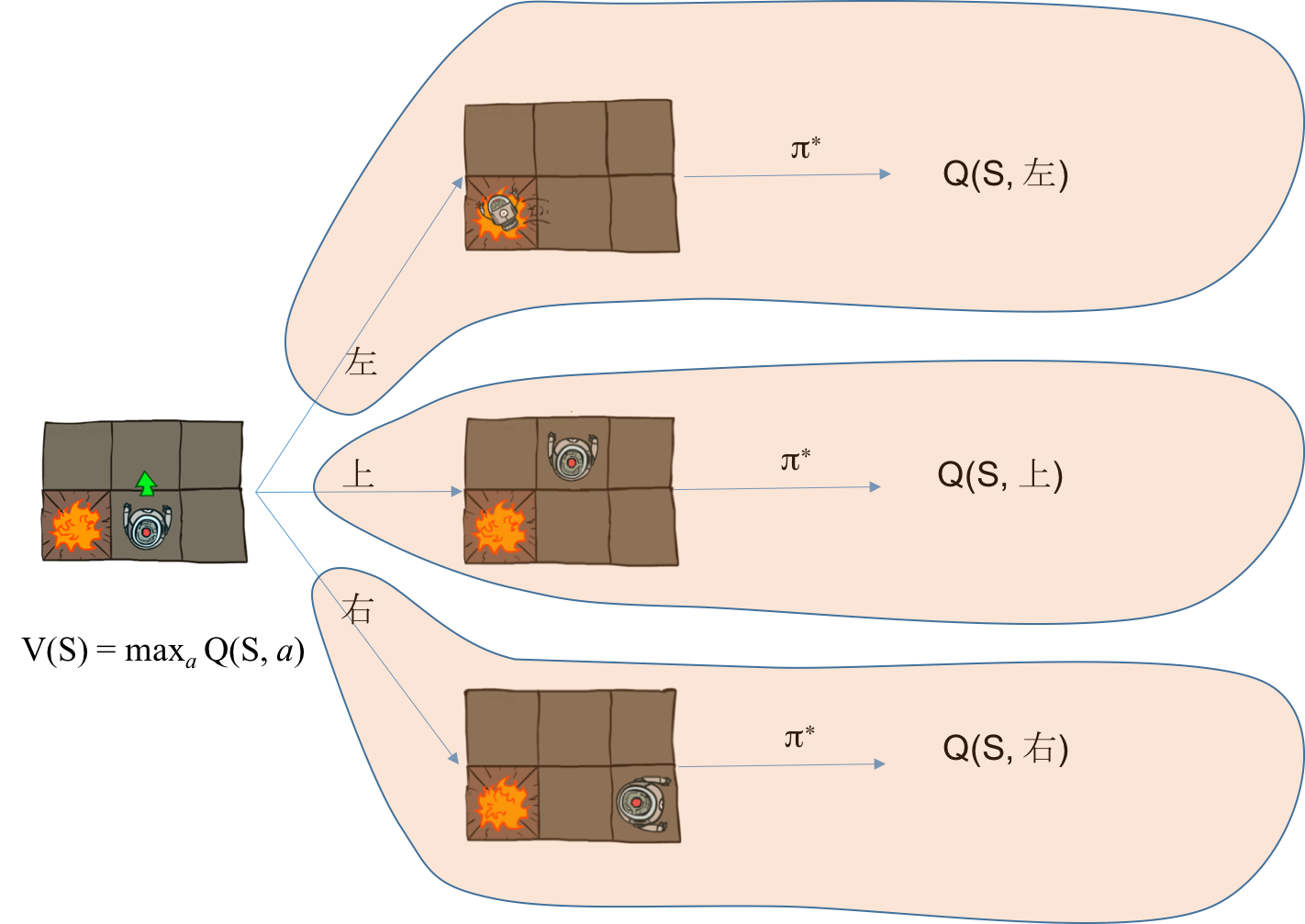
这两个关系表明，在环境已知的情况下，即转移概率P和回报函数R已知，Q和V可以互相转化，只要求出其中一个，另一个也就求出来了。

同理可以定义在具体策略$\pi$下的动作值函数为：从状态S出发，采用动作A后，然后在以后的决策中采用策略$\pi$选择动作，所能获得的期望回报！

$$
Q^{\pi}(S, A) = E \left[ \sum_{t=1}^{\infty} \gamma^{t-1} R(S_t, A_t, S' _ t) | S_1=S, A_1=A, A_t \sim \pi \right]
$$

与动作值函数的差别在于从第二步开始，动作按照策略$\pi$给出而不是最优策略。

HJB方程

利用动作值函数可以评估一个动作的好坏，给出最优策略。因此，如果我们能够求出Q函数，那么最优策略也就出来了；如果能够求出状态值函数，根据前面这两个值函数的关系，也可以得到Q函数，从而得到最优策略。那么怎么求出状态值函数呢？答案是利用值函数的递推关系，构建HJB方程。

利用状态值函数和动作值函数的两个关系可得

$$
\begin{align}
V(s) &= \max_a Q(s, a) \\
&= \max_a \sum_{s'} P(s'| s, a)[ R(s, a, s') + \gamma V(s') ]
\end{align}
$$

最后一个式子就是HJB方程，也有叫贝尔曼方程的。这个式子中，未知的是状态值函数V(s)，已知的是环境的状态转移概率P和回报R，由于存在求max操作，使得它是关于状态值函数的非线性方程！如果我们从这个方程中求解出状态值函数V(s)，那么最优策略的问题就引刃而解了！

确定性环境的HJB方程

如果环境是确定性的，即采用某个动作后转移到的状态是唯一的，在迷宫的例子中，相当于我可以直接控制机器人的运动，而不是通过语音来间接控制。那么上述HJB方程的求期望步骤可以省略，HJB方程变为

$$
V(s) = \max_a R(s, a, s') + \gamma V(s')
$$

s'是在状态s下采用动作a后转移到的状态，在确定性迷宫问题中，考虑s=14的例子，HJB方程就是说(记住 V(15)=0)

$$
V(14) = \max \{\gamma V(13), \gamma V(10), 1 \}
$$

对每一个状态s，都可以写出上述类似的非线性方程，我们可以得到14个这样的非线性方程构成的非线性方程组。那么怎么求解这种非线性方程呢？可能有些对算法比较熟悉的同学已经从上述表达式看出来了，这就是动态规划！

动态规划

采用动态规划求解HJB方程有两类方法，分别是值迭代和策略迭代。在一定条件下，他们都能收敛到最优解。

值迭代

值迭代的基本思想是，将HJB方程看做如下函数的不动点

$$
f(V) = \max_a \sum_{s'} P(s'| s, a)[ R(s, a, s') + \gamma V(s') ]
$$

V是一个向量，包含多个元素，这个函数是一个多变量非线性函数。函数f的不动点是指满足方程$f(x) = x$的解。根据压缩映像原理，如果函数f是压缩映象，那么对任何初始值$V_0$，可以不断地应用函数f迭代下去$V_{k+1} = f(V_{k})$，$V_k$必收敛于函数f的不动点！而f的不动点就是满足HJB方程的状态值函数，所以有值迭代算法

1. 初始化$V_0(i)=0, i=1,2,...$
2. 利用HJB方程迭代 $V_{k+1}(s) = \max_a R(s, a, s') + \gamma V_{k}(s')$
3. 重复第2步直到收敛！

当$\gamma<1$时，函数f一定是压缩映像，上述算法必收敛于不动点！不动点算法也是一个常用的求解非线性方程或线性方程的算法。下面简单介绍一下它的原理。

压缩映像原理

注意：理解本部分需要本科及以上数学功底，高中数学能力的请跳过，接受上述结论即可！

一个定义在巴拿赫空间B上的自映射f:B → B 是压缩映象是说，对任意两个$x, y \in B$，有

$$
d( f(x), f(y) ) \le \gamma d( x, y ), 0 < \gamma < 1
$$

d是距离测度，也就是说在这个映射下，像的距离比原像的距离短，就像在压缩一样，所以叫做压缩映像(也说映射)。

压缩映象有个不动点定理，说如果f是巴拿赫空间的压缩映象，那么必存在唯一的不动点x满足不动点方程$f(x) = x$。存在性我就不证明了，可以简单解释一下为什么会收敛到这个不动点。假设$x_0$是某个初始点，$x_k = f(x_{k-1})$，$x^ * $是不动点，那么根据压缩映象的定义，对任意正整数k有

$$
|| x_{k} - x^ * || = || f(x_{k-1}) - f(x^ *) || \\
< \gamma || x_{k-1} - x^ * || < ... < \gamma^k ||x_0 - x^ * || \\
\rightarrow 0 (k \rightarrow \infty)
$$

有兴趣的同学不妨利用类似的技巧证明一下值迭代在$\gamma<1$是收敛的。

这个性质可以用来求解非线性方程，下面是一个简单的计算$\sqrt{n}$例子。计算机只会加减乘除，其他数学运算都要表示为这四则运算才能计算，那么怎么计算$\sqrt{n}$。计算方法有很多，这里介绍利用压缩映像不动点的性质的计算方法。$\sqrt{n}$可以看做方程$x^2 = 2$的解，这个方程等价于 $x = 0.5(n/x + x)$。因此，x是函数$f(x) = 0.5(n/x + x)$的不动点。容易验证f是非线性函数，且是压缩映像。那么就可以令x0=1，不断地应用$x_k = f(x_{k-1})$迭代下去就可以了，最终就会收敛到$\sqrt{n}$！

策略迭代

策略迭代是另外一种求解HJB这个线性方程的方法，因为这个非线性方程的所有非线性来自于求最大值，前面说过，如果我们把策略固定，HJB方程的求最大值就消失了，变成线性方程！

$$
V^{\pi}(s) = \sum_{s'} P(s'| s, a)[ R(s, a, s') + \gamma V^{\pi}(s') ]
$$

线性方程很容易解决，从小学就开始学了，不停地代换消元即可，这就是高斯消元法。这个过程，称作策略评估，因为计算出来的是某个策略下的值函数，值函数可以来评估策略的好坏，所以叫策略评估。

当$V^{\pi}$计算好了之后，我们又可以通过它得到一个新的策略

$$
\pi'(s) = \arg\max_a Q^{\pi}(s, a)
$$

因为Q函数和V函数可以知一求二，前面知道了V函数，利用V和Q的关系很容易得到Q，然后就可以计算这个新的策略了。可以证明这个策略不会比之前的策略差，也就是对所有状态s，两个策略的值函数满足$V^{\pi}(s) \le V^{\pi'}(s)$，因此只要不断地迭代下去，也可以得到最优的策略！这一步叫做策略提升，因为新的策略效果提升啦！

综合这两步，我们就得到策略迭代算法：

1. 初始化一个策略$\pi$
2. 通过解线性方程计算策略$\pi$的值函数V和Q
3. 从Q函数中得到新的策略，更新到$\pi$中
4. 重复 2-3 直到策略收敛！

两种迭代法的对比

这两种迭代法本质都是在求解HJB方程，得到值函数的值，因为状态是有限的，所以值函数就是一个向量。得到值函数之后，就可以得到最优策略了。值迭代只有一个迭代，反复使用HJB方程进行迭代，直到收敛就可以了。而策略迭代先固定策略，接线性方程得到值函数，然后利用值函数来提升策略，这两个步骤反复迭代，直到找到最优策略。策略迭代通常的迭代次数会比值迭代要少，但是内部接线性方程耗时会比较多，两种迭代方法都在一定条件下可以收敛到最佳策略。在实践部分，我们将实现这两个算法，初始代码和环境已经准备好了，你只需要是想这两个算法就行。

环境未知的问题

前面我们讲到，如果环境已知，也就是转移概率P和回报函数R已知，我们可以通过求解HJB方程得到值函数，进而得到最优策略。但是如果我们不知道环境会对我们做出如何反馈，就像身在迷宫中的机器人，看不到全貌。那么我们该如何得到值函数和最优策略呢？答案是通过蒙特卡罗模拟，估计出环境的转移概率P和回报函数R。因为状态是有限的，动作也是有限的，所以只要用很多个机器人采用完全随机的策略进行尝试，那么根据尝试的结果，可以估计出转移概率和回报函数。假设随机尝试了很多很多次，每一次采取动作都会得到一个四元组(S', A', S', r)。例如在迷宫问题中，从动作1开始，采用向右(A=4)，到达状态2，环境回报为-1.那么这个四元组就是(1,4,2,-1)。当得到很多这样的四元组后，就可以统计每一对(S, A)转移到S'的次数N(S, A, S')和遇到的所有(S, A)的次数N(S, A)，从而得到概率和回报

$$
P(S'|S, A) = \frac{ N(S, A, S') }{\sum_{s'} N(S, A, s')} \\
R(S, A, S') = r
$$

例如，从状态1出发，采用动作4(向右)，有90次转移到了状态2，有10次转移到了状态5，所以可以估计出P(1,4,2)=0.9, P(1,4,5)=0.1, P(1,4, 其他状态)=0。这些可能的状态转移带来的回报都是-1，所以R(1,4,所有状态)=-1。

一旦我们通过上述模拟方法得到对环境的估计，那么就可以采用上述动态规划方法求解出值函数，进而得到最优策略！

强化学习的解释

强化学习和传统的监督学习方式有所不同，它没有一个很强的监督信号告诉模型，要拟合一个什么样的函数？也不像无监督学习完全没有反馈，强化学习有一个弱的反馈信号告诉你，你采取的动作是对的还是错的，就像一只被训练接铁饼的小狗，如果它不接住铁饼，将会受到一个惩罚，相反，如果它接住了铁饼，或者主动去追铁饼，将会收到一个奖励。这种反馈机制，让小狗虽然一开始不知道要干什么，但是经过不断的尝试-失败，不断地探索，它将最终知道自己要追逐的目标是什么。而监督学习就是有一个老师，先示范一下告诉小狗要做什么，然后让小狗跟着做。无监督学习则既没有老师，也没有反馈，所以小狗也不知道要干啥，它只会做自己熟悉的事情。从这个角度来看，强化学习是在无监督学习和监督学习中间的一种半监督学习。

从实现来看，强化学习与监督学习不同的是，它有动作！也就是有主观能动性，监督学习则是被动地接受老师教给的知识，没有充分利用主官能动性。监督学习从一开始就知道学习的目标精确的是什么，比如做人脸识别，你一开始就知道这张图片是不是人脸，模型要做的就是建立一个函数输出是人脸还是不是人脸。而强化学习是要建模策略函数，在一开始是不知道哪个策略是对的还是错的，只有尝试之后，收到环境的反馈后，才知道这种尝试是否正确。这种反馈是通过和环境交互得到的，而不是我们“误差冒泡”的算法中给出的。拿人脸识别来说，监督学习就是已经有很多标注的人脸和非人脸照片，你去训练一个模型，拟合这个输入和输出。而强化学习则是你不知道这个任务是干什么，只是给你图片，可以和我互动，我不会直接告诉你答案，你可以通过观察我的表情来得到一部分关于猜对还是猜错的信息。

从应用场景来看，监督学习主要是来做预测的，而强化学习主要是来做决策的。监督学习可以先预测，然后根据预测的结果信息然后进行决策。而强化学习则直接给出策略。因此从这种角度来看，似乎强化学习更加直接。例如在做搜索排序，监督学习会拟合一个得分，然后你根据这个得分从大到小排序，或者在加上一些其他策略。但是显然这种不是最优的，比如得分很高的都是一些非常相似的东西，都排在前面是没什么意义的。而强化学习直接拟合排序策略，将监督学习人工决策的过程也干了，因此可能得到更好的效果。

强化学习与深度学习的关系：实际上强化学习和深度学习是对机器学习算法两个完全不同的分类方式。强化学习是与监督学习和无监督学习一个范畴的，而深度学习则是从学习的模型层面上进行划分，是与决策树、浅层模型一个范畴的。强化学习是一种学习的通用方法，不限制用什么模型，而深度学习时特指用某类模型而没有说用什么学习方法。强化学习可以和深度学习模型结合起来，就是深度强化学习，AlphaGo的创始人之一曾在ICML大会上说AI=DL(深度学习) + RL(强化学习)，可见强化学习和深度学习的重要地位。

强化学习的应用

有注意力的图像识别系统

在监督学习中，我们说到一个模型就是在拟合一个函数，输入是一些特征，图像的数字表示就是它的特征，图像在计算机中都是用很多数字表示，如果是黑白图像，每一个像素是一个数值，数值大小表示明暗。图像识别就是在拟合这样一个函数，输入是图像，输出是图像的类别。对于一张高清图片，往往需要降低分辨率，减少计算量，或者分成很多子块，进行分类，然后再把字块识别的结果融合起来。那么怎么选择子快呢？最简单的方法是随机按照不同位置不同分辨率选出很多子块，一种更好的方案是第一个子块可以根据整个图像的低分辨率选取，接下来每次选取的位置根据之间看到的所有子块共同决定，这样每次选择哪个字块就可以看做马尔科夫决策过程。状态(S)是我之前看过的所有图片，动作(A)是我选择的字块的位置（假设字块的大小被固定），回报(R)是我最终的识别是否准确，识别对了回报为1，否则为0。这就是Google在2014年再论文 Recurrent Models of Visual Attention 中所用的方案。他把每次查看的字块的机制叫做注意力机制，就像我们人来识别图片中的内容时，目光的焦点会在图片中不断跳动，每一次跳动就可以看做我们的一次决策过程。

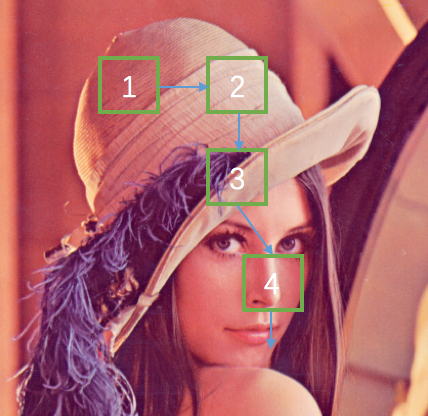
思考与实践

1. 考虑如下图所示的MDP问题，S是初始状态，G是终止状态，对于非终止状态，每个状态可以采取两个动作：左或者右，每一步的回报都是-1。其中中间有一个状态，采取的动作和实际运动方向是相反的，也就是动作是向左，而实际运动是向右，其他两个状态正常。一个随机策略$\pi$定义如下：每一次都随机地以概率p选择动作“右”，以概率(1-p)选择动作“左”。试推导$V^{\pi}(S)$的最大值和此时的概率p的值。参考答案：p=0.59, V=-11.6。

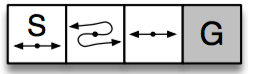
1. 编程实现值迭代和策略迭代算法

构建一个简单的模拟环境，有nS个状态，0，1，...，nS-1；其中nS-1是终止状态。该环境下一共两个动作：0向左运动，1向右运动，每个动作都有概率p0不动，p1的概率会往反方向运动, 1-p0-p1概率正常运动。

import numpy as np

nS = 10
nA = 2  #不要改这个参数
Done = nS - 1
p0 = 0.1
p1 = 0.1
P = np.zeros((nS, nA, nS)) # 转移概率
R = np.zeros((nS, nA, nS)) - 1.0 # 回报都是-1
gamma = 1

# 环境构建
for s in range(nS):
    if s == Done: # 终止态转移概率都为0
        continue
    for a in range(nA):
        inc = a * 2 - 1 # 步长        
        P[s, a, s] += p0 # 不动
        P[s, a, max(0, s - inc)] += p1 # 反方向
        P[s, a, max(0, s + inc)] += 1 - p0 - p1 # 正常运动



V = np.zeros(nS)
# 值迭代
for it in range(1000):

    ## YOUR CODE HERE

    ## END
    pass

print 'iteral steps:', it
print V





# 策略迭代

pi = np.zeros(nS, dtype=int) #初始策略全部往左

for it in range(100):
    V = np.zeros(nS)
    # 策略评估，解线性方程

    ## YOUR CODE HERE

    ## END

    # 策略提升

    ## YOUR CODE HERE

    ## END

print 'pi =', pi
print 'V =', V