简介

• 大佬：杨强
• 迁移学习：两个领域存在一定的相似性。举一反三
• 负迁移：两个领域存在一定的相反性。东施效颦
• 远领域迁移学习：通过多个中间任务，将两个不像似的任务串联起来，实现远邻域迁移（可以实现用人脸识别来识别飞机）

• 应用：

  • 机器翻译，语料不足
  • 图像识别，不同光照、背景
  • 行为识别

• 迁移学习 (Transfer Learning): 给定一个有标记的源域 Ds = {xi , yi }ni=1 和一个无 标记的目标域 D = {x }n+m 。这两个领域的数据分布 P(x ) 和 P(x ) 不同，即 P(x ) ̸=
  tjj=n+1 sts P (xt )。迁移学习的目的就是要借助 Ds 的知识，来学习目标域 Dt 的知识 (标签)。

• 一句话总结: 相似性是核心，度量准则是重要手段。
• 度量准则
  • MMD：Maximum mean discrepancy
  • Principal Angle
  • A-distance
  • Hilbert-Schmidt Independence Criterion
  • Wasserstein Distance

基本方法

• 分类：基于样本、基于模型、基于特征、基于关系

基于样本

• 源域中存在不同种类的动物，如狗、鸟、猫等，目标域只有狗这一种类别。在迁移时，为了 最大限度地和目标域相似，我们可以人为地提高源域中属于狗这个类别的样本权重。

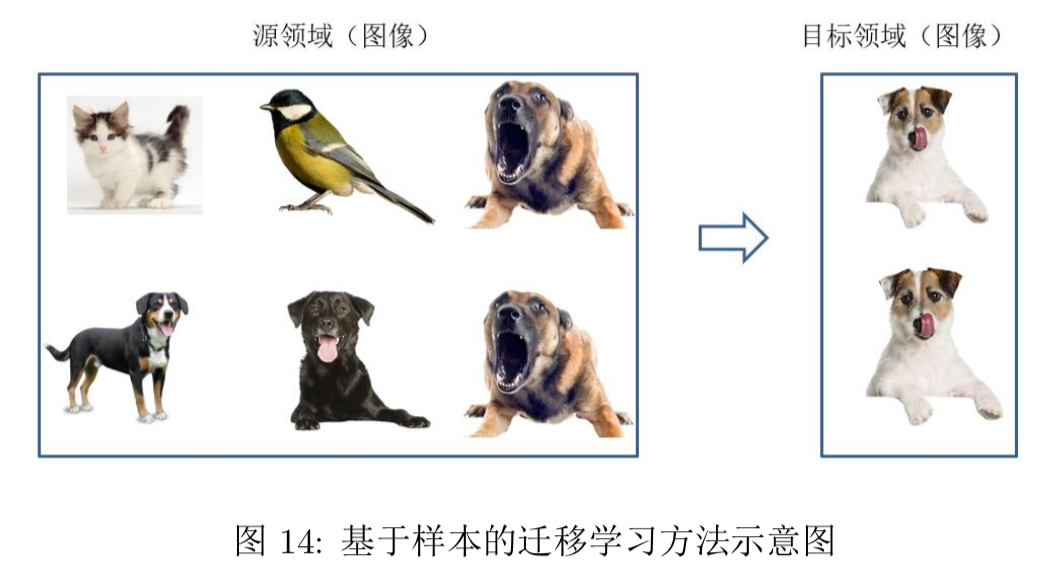
• 理论上对源域s的样本做加权$(P(x_t)/P(x_s))$，就可以得到目标域的样本分布，从而在源域加权后的样本中训练就实现了IID
• 应用局限：只在两个域差异较小的时候可以用，在NLP，CV等领域效果不好

基于特征

• 基于特征变换，减少两个域的特征差异
• 将两个域的特征映射到同一个特征空间中

基于模型

• 指从源域和目 标域中找到他们之间共享的参数信息，以实现迁移的方法。

基于关系

• 略

第一类方法:数据分布自适应

边缘分布自适应

• 基本思想，因为$(P(x_s))$ 和 $(P(x_t))$ 不一样，所以期望存在某种隐射$(\phi)$ 使得 $(P(\phi(x_s))=P(\phi(x_t)))$，并假设边缘分布一致时条件分布也一样。
• TCA：学一个映射$(\phi)$，使得源域与目标域特征距离最小
  $$
  ||\frac{1}{n_s}\sum \phi(x_i^s) - \sum \phi(x_j^t)||_H
  $$
  那么在源域学到的预测模型，就可以在目标域中进行预测了。

统计特征对齐

• 找个变换M，将$(X_s)$ 隐射到 $(X_t)$

流行学习

• Grassman流行
• SGF：把源域和目标域分别看成高维空间 (即 Grassmann 流形) 中的两个点，在这两个点的测地线距离上取 d 个中间点，然后依次连接 起来。这样，源域和目标域就构成了一条测地线的路径。我们只需要找到合适的每一步的变 换，就能从源域变换到目标域了。
• 简单地说就是找到一系列变换可以将源域的点沿着测地线变换到目标域的点

深度迁移学习

finetune

• 最简单的深度网络迁移形式:finetune。即在A任务上训练好的前n层微调。
• 神经网络的前 3 层基本都是 general feature，进行迁移的效果会比较好;
• 深度迁移网络中加入 fine-tune，效果会提升比较大，可能会比原网络效果还好;
• Fine-tune 可以比较好地克服数据之间的差异性;
• 深度迁移网络要比随机初始化权重效果好;
• 网络层数的迁移可以加速网络的学习和优化。

深度网络自适应

• 增加了一个自适应损失项

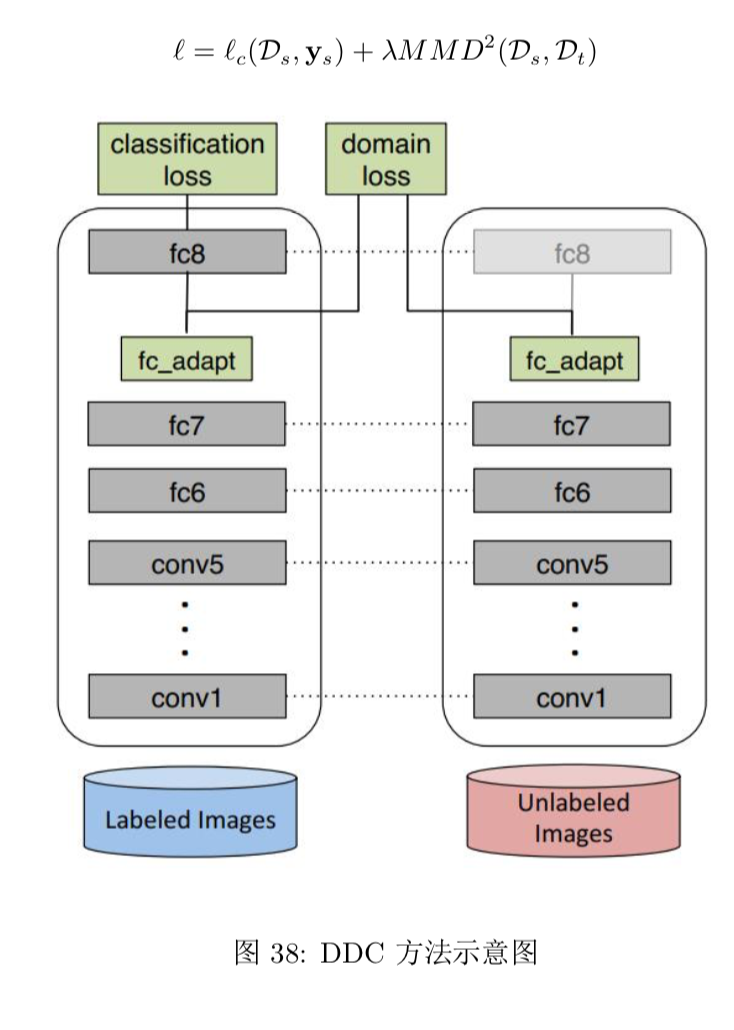
• DAN:有别于 DDC 方法只加入一个自适应层，DAN 方法同时加入了三个自适应层 (分类器前 三层);多核 MMD 度量 (MK-MMD)
• Joint Adaptation Network:JMMD 度量 (Joint MMD)
• AdaBN: AdaBN(Adaptive Batch Normalization) [Li et al., 2018]， 通过在归一化层加入统计特征的适配，从而完成迁移。

深度对抗网络迁移

FAQ

迁移学习的本质是什么

• 训练集和测试不是同分布，但是有关系的学习任务
• 找到源领域与目标领域数据的相似性和不变量

TDC方法为什么目标域没有label也能学习

• TODO