Explore Exploit 探索与利用 - Tracholar的个人wiki

Explore 和 Exploit 是做推荐的常用问题,由于推荐的点击率/转化率模型是由历史数据产生的,对新的item点击率估计误差会很大,需要对曝光不足的item进行探索。

考虑多臂老虎机问题,即有N个老虎机,每个臂有概率 Pi 会有奖励,并且这个概率不随时间变化。

显然,最优策略是选择概率 Pi 最大的那个臂不停地摇,每次期望回报最大 $(r^* = \max_i p_i)$,
而由于一开始不知道 Pi ,所以实际第t步的回报期望可能小于最大值。定义 $(r_t)$为第t步的回报,如果有奖励,回报为1,否则回报为0.
其期望值等于摇的那个臂对应的 Pi 的值。

可以定义 regret 为他们的差 $(regret_t = r^* - E r_t)$。

## 多臂老虎机仿真
import numpy as np

n = 10 # 10个臂
bandit_p = np.random.rand(n)

def gen_data(i):
    assert i < n
    if np.random.rand() < bandit_p[i]:
        return 1.0  # reward
    return 0.0 # no reward

在这个问题中,一般有这些经典的探索方法:

随机策略:随机选择一个动作,简称瞎猜,每一个动作都有概率。所以 $( regret = \max_i p_i - \bar{p_i} )$

def random_select(ctx):
    return np.random.randint(ctx['n'])

确定性策略:每次都选择当前最优的动作,如果最优动作很多个,随机选一个

# 稍作修改,前n次依次选择每一个动作
def determine_select(ctx):
    if ctx['step'] < n:
        return ctx['step']
    return np.argmax(ctx['cum_reward_action'] / (ctx['cum_action']))

$(\epsilon)$-贪心策略:即以 $(\epsilon)$ 的概率选择随机策略,以 $(1 - \epsilon)$选择确定性策略, $(\epsilon)$ 随着时间衰减

def epsilon_greedy(ctx):
    epsilon = 1 / (1 + np.sqrt(ctx['step']))
    if np.random.rand() < epsilon: # random
        return random_select(ctx)
    else:
        return determine_select(ctx)

naive 策略: 前N步随机探索, 从第 N+1 步开始,采用确定性策略

def naive_select(ctx):
    if ctx['step'] < 500:
        return random_select(ctx)
    else:
        return determine_select(ctx)

softmax 随机策略:即对每一个动作的累积平均回报做softmax归一化,作为每个动作的选择概率

def softmax_select(ctx, n0 = 0.1):
    if ctx['step'] < n:
        return ctx['step']
    avg_reward = ctx['cum_reward_action'] / (ctx['cum_action'])
    p = np.exp(avg_reward / n0 )
    p = p / np.sum(p)
    return np.random.multinomial(1, p)[0]

thompson 采样: 认为每个动作的Pi 服从Beta(a, b)先验分布, 而每个动作的历史平均回报后验分布则服从 Beta(a + win, b + loss) 分布,确定性策略相当于按照后验分布的均值/众数选择最优策略,然而前期由于探索不充分,这种估计方差很大,必然要引入随机性进行探索,Thompson的方法是从后验分布中采样一个值代替对Pi的估计,然后按照确定性策略选择动作。

def thompson_select(ctx):
    win = ctx['cum_reward_action']
    loss = ctx['cum_action'] - win
    p = np.zeros(n)
    for i in range(n):
        # 期望概率 p_i = (1 + win[i]) / (1 + trials[i]), 现在不是用期望的概率,而是引入一定的随机性,随机从p_i服从的后验beta分布中采样一个结果
        p[i] = np.random.beta(1 + win[i], 1 + loss[i])
    return np.argmax(p)

UCB方法: 因为利用历史平均回报对Pi估计不准,所以可以用估计的置信区间的上界 $(\bar{r_i} + \sqrt{\frac{2 ln T}{n_i}})$ 作为对Pi的乐观估计。
然后采用确定性策略。其中 T 是总的步数, n_i 是第i个臂被选择的次数。

def ucb_select(ctx):
    if ctx['step'] < n:
        return ctx['step']
    cum_n = ctx['step'] + 1.0
    up_bound = ctx['cum_reward_action'] / (ctx['cum_action']) + np.sqrt(1.0 * np.log(cum_n) / ctx['cum_action'])
    return np.argmax(up_bound)

仿真代码

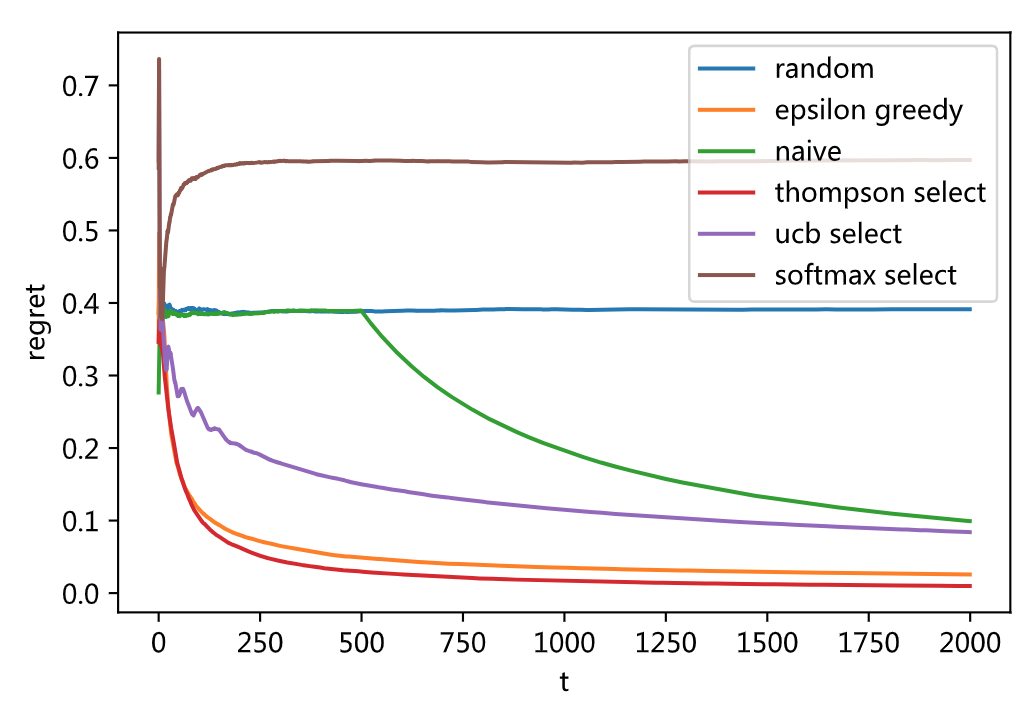
import matplotlib.pyplot as plt
from numba import jit
import logging

@jit
def simulation(select_action, n_ = 3000):
    t = []
    reward = []
    cum_reward_per = 0.0
    cum_reward_action = np.zeros(n)
    cum_action = np.zeros(n)
    for i in range(n_):
        t.append(i)
        ctx = {'n' : n, 'cum_reward_action' : cum_reward_action, 'cum_action' : cum_action, 'step': i}
        action = select_action(ctx)
        cum_action[action] += 1
        r = gen_data(action)
        action_n = cum_action[action]
        cum_reward_action[action] += r
        cum_reward_per += r
        reward.append(cum_reward_per)
    return np.array(t), np.array(reward)

@jit
def run(select_action, rnd_ = 100, n_ = 3000):
    t = []
    avg_reward = 0
    for i in range(rnd_):
        t, reward = simulation(select_action, n_)
        avg_reward = avg_reward * i / (i + 1) + reward / (i+1)

        logging.info("simulate %d round." % (i))
    return t, np.max(bandit_p) - avg_reward /(1 + np.arange(n_))


def main():
    n_ = 2000
    t, r = run(random_select, n_ = n_)
    plt.plot(t, r)

    t, r = run(epsilon_greedy, n_ = n_)
    plt.plot(t, r)

    t, r = run(naive_select, n_ = n_)
    plt.plot(t, r)

    t, r = run(thompson_select, n_ = n_)
    plt.plot(t, r)

    t, r = run(ucb_select, n_ = n_)
    plt.plot(t, r)

    t, r = run(softmax_select, n_ = n_)
    plt.plot(t, r)


    plt.legend(['random', 'epsilon greedy', 'naive', 'thompson select', 'ucb select', 'softmax select'])
    plt.xlabel('t')
    plt.ylabel('regret')
    plt.show()

if __name__ == '__main__':
    main()

ee simulation