强化学习

关于

强化学习是未来很重要的方向！参考 Alpha Go！

Markov Decision Process

• A set of states $(s \in S)$
• A set of actions $(a \in A)$
• A transition function $(T(s, a, s'))$
  • 转移概率 $(P(s'| s, a))$
  • 也叫 model 或者 dynamics
• A reward function $(R(s, a, s'))$
  • 通常只是状态的函数$(R(s), R(s'))$
• 一个初始状态
• 一个终止状态

MDP 不是一个确定性的搜索问题，一种方法是 期望值最大搜索 ？！

马尔科夫性说的是未来的决策与过去无关，至于当前状态和策略有关！

（最优）策略：$(\pi^* : S \rightarrow A)$

状态转移函数 $(T(s, a, s') = p(s'| s, a))$

discounting reward: $(r_0 + \gamma r_1 + \gamma^2 r_2 + ...)$

当 $(\gamma < 1)$时，discounting reward 有界 $(R_{max}/(1-\gamma))$！

或者采用 finite horizon，当迭代到 T 步时，停止！

• MDP quantities:

  • Policy = 对每一个状态选择一个action
  • Utility = sum of (discounted) rewards

• 状态 value function： $(V^* (s))$

• q-state (s, a), $(Q^* (s,a))$

• 最优策略 $(\pi^* (s))$

• 递归定义：

  • $(V^ * (s) = \max_a Q^ * (s, a))$
  • $(Q^ * (s, a) = \sum_{s'} (s, a, s') \left[ R(s, a, s') + \gamma V^* (s') \right])$
  • $(V^ * (s) = \max_a \sum_{s'} (s, a, s') \left[ R(s, a, s') + \gamma V^* (s') \right])$

• Time-limited value: 定义$(V_k(s))$ 为状态s下，最多k步下的最优value

• Value iteration:
  1. $(V_0(s) = 0)$
  2. $(V_{k+1}(s) \leftarrow \max_a \sum_{s'} (s, a, s') \left[ R(s, a, s') + \gamma V_k^* (s') \right]) )$
  3. 重复1-2直到收敛！
  4. 复杂度，每次迭代 $(O(S^2A))$
  5. 收敛到唯一最优值！贝尔曼算子在 $(\gamma<1)$时时压缩算子，所以必收敛到不动点。
• Policy iteration
  1. 随机化策略$(\pi)$
  2. Policy evaluation：对给定的策略 $(\pi)$，利用迭代或者线性方程求解的方法计算该策略下的值函数，即求解下面第一个方程。因为该方程是一个关于值函数的线性方程，所以对于有限状态的情况可以直接求解线性方程，或者利用迭代求解。
  3. Policy improvement：对上述值函数，利用贝尔曼方程求出最优策略。重复2-3多次直到收敛，收敛条件是策略不改变了。
     实际上，它是在交替迭代策略和值函数。这种方法可以保证每次迭代值函数单调不减，又因为有界所以收敛。

$$
V^{\pi_i}(s) = r(s, \pi_i(s)) + \gamma \sum_{s' \in S} p(s'|s, \pi_i(s)) V^{\pi_i}(s') \\
\pi_{i+1}(s) = \arg \max_a r(s, a) + \gamma \sum_{s' \in S} p(s'|s, a) V^{\pi_i}(s')
$$

Reinforcement Learning

仍然是一个MDP过程，仍然寻找最优决策！
但是不知道状态转移函数T 和 回报函数 R！

• MDP：Offline
• RL：Online

model-based Learning

通过经验，学习一个近似模型，然后求解！

• Step1：学习经验MDP模型：
  1. 对每一个个(s, a)统计s'
  2. 归一化得到$(\hat{T}(s, a, s'))$
     3.

深度强化学习tutorial@ICML2016

AI = RL + DL

• 值函数
• 策略
• 状态转移模型

使用深度学习建模值函数，策略和模型！

Value-Based Deep RL

Q-Networks

$$
Q(s, a, w) \approx Q^* (s, a)
$$

Q-Learning：

最优 Q-value 应该遵循 Bellman 方程

$$
Q^ * (s, a) = \mathbb{E}_{s'} \left[ r + \gamma \max_{a'} Q(s', a')^ * |s, a \right]
$$

其中 s 表示状态，a 表示agent对环境做出的 action！
将方程右边当做目标，用神经网络学习！
损失函数：

$$
l = (r + \gamma \max_{a'} Q(s', a', w) - Q(s, a, w) )^2
$$

问题：1. 训练样本不是 iid； 2. 目标不稳定！

DQN：利用 agent 自身经验构建样本！

$$
l = \left(r + \gamma \max_{a'} Q(s', a', w^-) - Q(s, a, w) \right)^2
$$

在某一次replay 的更新中，$(w^-)$是固定的！replay结束后，将线上的权值$(w)$更新到$(w^-)$

Double DQN

• 当前的 Q-network w 用来选择 action
• 老的 Q-network w- 用来评估 action

$$
a^* = \arg\max_{a'} Q(s', a', w) \\
l = \left( r + \gamma Q( s', a^ * , w^- ) - Q(s, a, w) \right)^2
$$

Prioritised replay

按照 TD-error 对 replay memory 中的样本进行 importance sampling。

$$
\delta = \left| r + \gamma \max_{a'} Q(s', a', w^-) - Q(s, a, w) \right| \\
P(i) = \frac{p_i^{\alpha}}{\sum_k p_k^{\alpha}} \\
p_i = \delta_i + \epsilon
$$

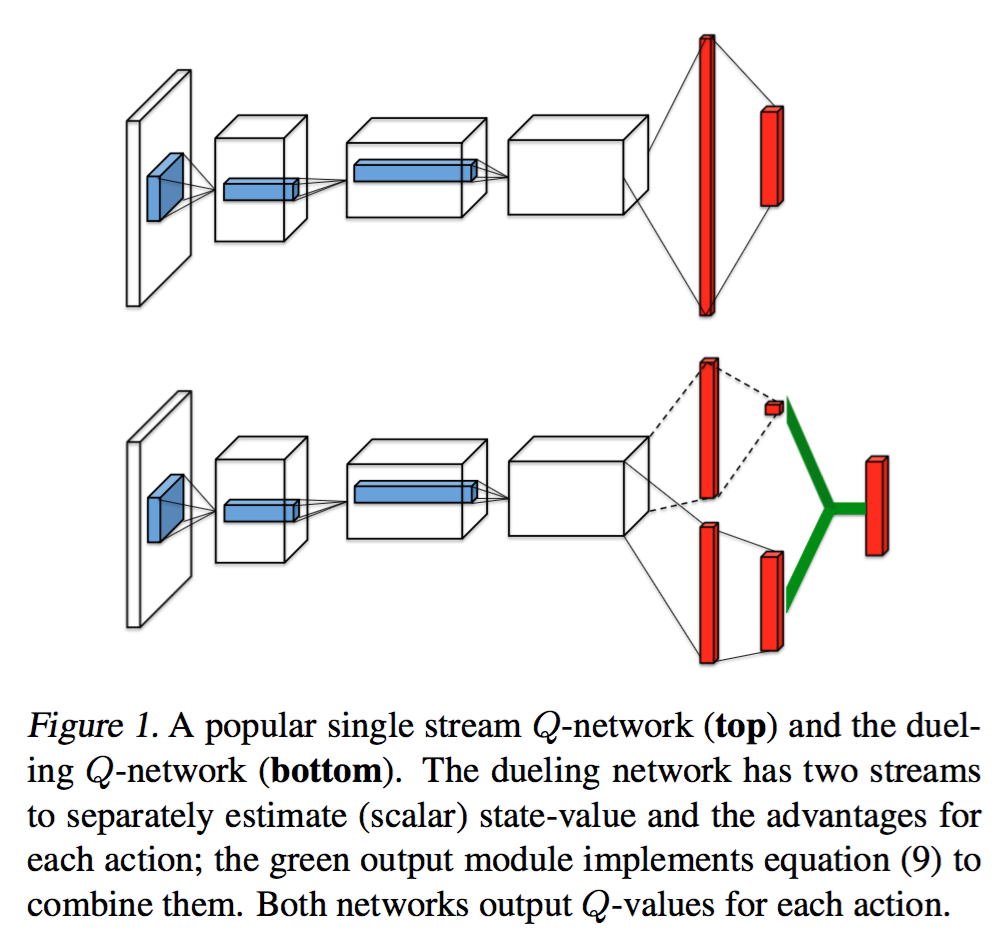
Duelling network

将 Q 函数分解为状态值函数与 advantage function（不知道怎么翻译） 之和。

$$
Q(s,a; \theta, \alpha, \beta) = V(s; \theta, \alpha) + A(s,a; \theta, \alpha)
$$

上式V和A之间是不定的，可以相差一个任意常数，不影响结果。为此，有两种解决方案，减最大值和平均值。
平均值方案更加稳定，因为V只需要跟踪平均波动，而不是最大波动。

$$
Q(s,a; \theta, \alpha, \beta) = V(s; \theta, \alpha) + \left( A(s,a; \theta, \alpha) - \max_{a'\in \mathcal{A}} A(s,a'; \theta, \alpha) \right) \\
Q(s,a; \theta, \alpha, \beta) = V(s; \theta, \alpha) + \left( A(s,a; \theta, \alpha) - \frac{1}{|\mathcal{A}|} \sum_{a'} A(s,a'; \theta, \alpha) \right)
$$

Deep Policy Networks

用神经网络建模策略函数

$$
a = \pi(a| s, \mathbf{u}) = \pi( s, \mathbf{u})
$$

目标函数为total discounted reward

$$
J(u) = \mathbf{E}(r_1 + \gamma r_2 + \gamma^2 r_3 + ... | \pi(., u))
$$

令$(\tao = (s_1, a_1, ..., s_t, a_t))$代表状态-动作路径，用$(r(\tao))$代表每个路径的折扣reward，那么期望回报函数

$$
J(\theta) = \int \pi_{\theta}(\tao) r(\tao) d\tao
$$

对参数$(\theta)$求导，由于回报函数与参数无关，所以梯度只作用与策略函数

$$
\nabla_{\theta} J(\theta) = \int \nabla_{\theta} \pi_{\theta}(\tao) r(\tao) d\tao =\int \pi_{\theta}(\tao) \nabla_{\theta} \log \pi_{\theta}(\tao) r(\tao) d\tao = E_{\tao ~ \pi_{\theta}(\tao)} \nabla_{\theta} \pi_{\theta}(\tao) r(\tao)
$$

利用马尔科夫性，

$$
\log \pi_{\theta}(\tao) = \log p(s_1) + \sum_{t=1}^T \left[\log \pi_{\theta}(a_t|s_t) + \log p(s_{t+1}|s_t, a_t) \right]
$$

代入上式可得

$$
\nabla_{\theta} J(\theta) = E_{\tao ~ \pi_{\theta}(\tao)} \sum_{t=1}^T \nabla_{\theta}\log \pi_{\theta}(a_t|s_t) r(\tao)
$$

如果把策略函数看做在状态s下选择动作a的概率，回报是该样本的权重！即加权极大似然估计！

相关资料

• 强化学习书籍：https://webdocs.cs.ualberta.ca/~sutton/book/ebook/the-book.html
• Tutorial: Deep Reinforcement Learning， ICML 2016. David Silver, Google Deepmind.
• CS234: Reinforcement Learning http://web.stanford.edu/class/cs234/index.html
• Berkeley 课程：CS 294: Deep Reinforcement Learning. http://rll.berkeley.edu/deeprlcourse/
• http://ai.berkeley.edu/course_schedule.html

created in 2016-09-04