An Empirical Evaluation of Thompson Sampling

Table of Contents

关于

UCB方法: 强理论保证
- P. Auer, N. Cesa-Bianchi, and P. Fischer. Finite-time analysis of the multiarmed bandit problem. Machine learning, 47(2):235–256, 2002.
- T.L. Lai and H. Robbins. Asymptotically efficient adaptive allocation rules. Advances in applied mathematics, 6:4–22, 1985.
贝叶斯优化版的Gittins: 在给定先验分布直接优化最大回报
- John C. Gittins. Multi-armed Bandit Allocation Indices. Wiley Interscience Series in Systems and Optimization. John Wiley & Sons Inc, 1989.
probability matching: Thompson sampling, 根据概率选择某个臂, 容易实现, 但缺乏理论分析
- William R. Thompson. On the likelihood that one unknown probability exceeds another in view of the evidence of two samples. Biometrika, 25(3–4):285–294, 1933.

上下文$(x)$, 动作集合A, 回报r, 多臂老虎机问题实际上是单步MDP, 上下文实际上就是状态
过去的经验 D由三元组 $( (x_i, a_i, r_i) )$ 构成, 由函数$(P(r|a,x,\theta))$建模,其中$(\theta)$是模型参数
设模型参数的先验分布为$(P(\theta))$
那么根据贝叶斯法则,后验分布$(P(\theta|D) \propto \Pi_i P(r_i|a_i,x_i,\theta) P(\theta) )$
如果我们知道理想的参数值$(\theta^* )$,那么我们应该选择使得期望收益最大的动作$(\max_a E(r|a,x,\theta^*) )$
但是实际上最优的参数是未知的, 可以最大化经验分布下的期望收益(即 exploitation) $(\max E(r|a,x) = \int E(r|a,x,\theta) P(\theta|D) d\theta)$
如果在探索的设置下,则是根据是最优动作的概率随机选择一个动作。即选择动作a的概率等于

$$
\int I[E(r|a,x,\theta) = \max_{a'} E(r|a',x,\theta)] P(\theta|D) d\theta
$$

汤普森采样

贝努力bandit

汤普森采样方法对先验分布参数的鲁棒性: 十分鲁邦
汤普森采样是渐进最优的, 比UCB具有更低的regret
EE的核心思想是: 提升选择那些我们不是很确定的动作的概率
乐观汤普森采样: 如果采样的score小于均值(即该动作当前的期望回报), 那么就截断到均值。
- 替换算法1中的$(E_r(r|x_t,a_t,\theta^t))$为 $(max( E_r(r|x_t,a_t,\theta^t), E_r(r|x_t, a_t) ))$

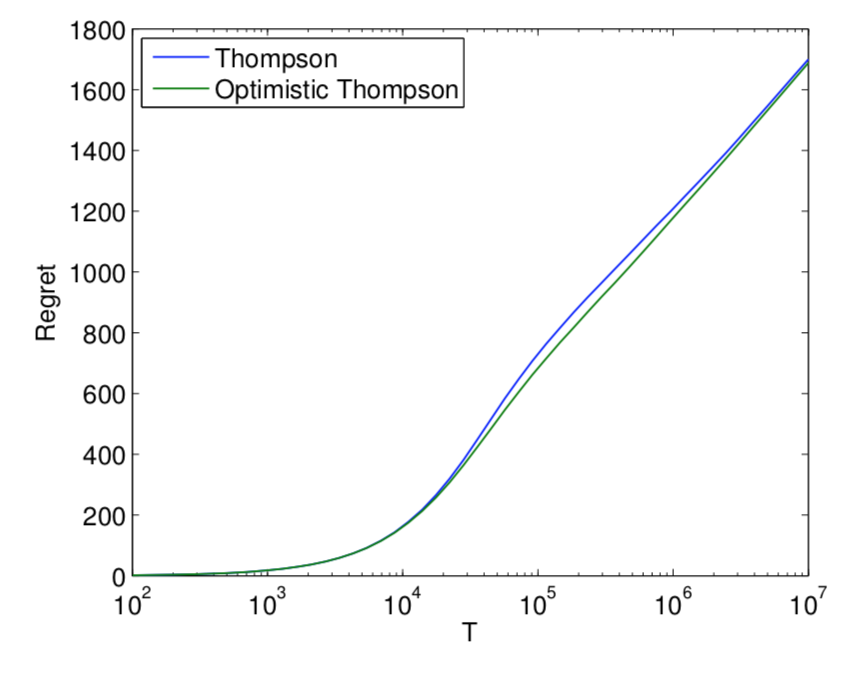
乐观汤普森采样

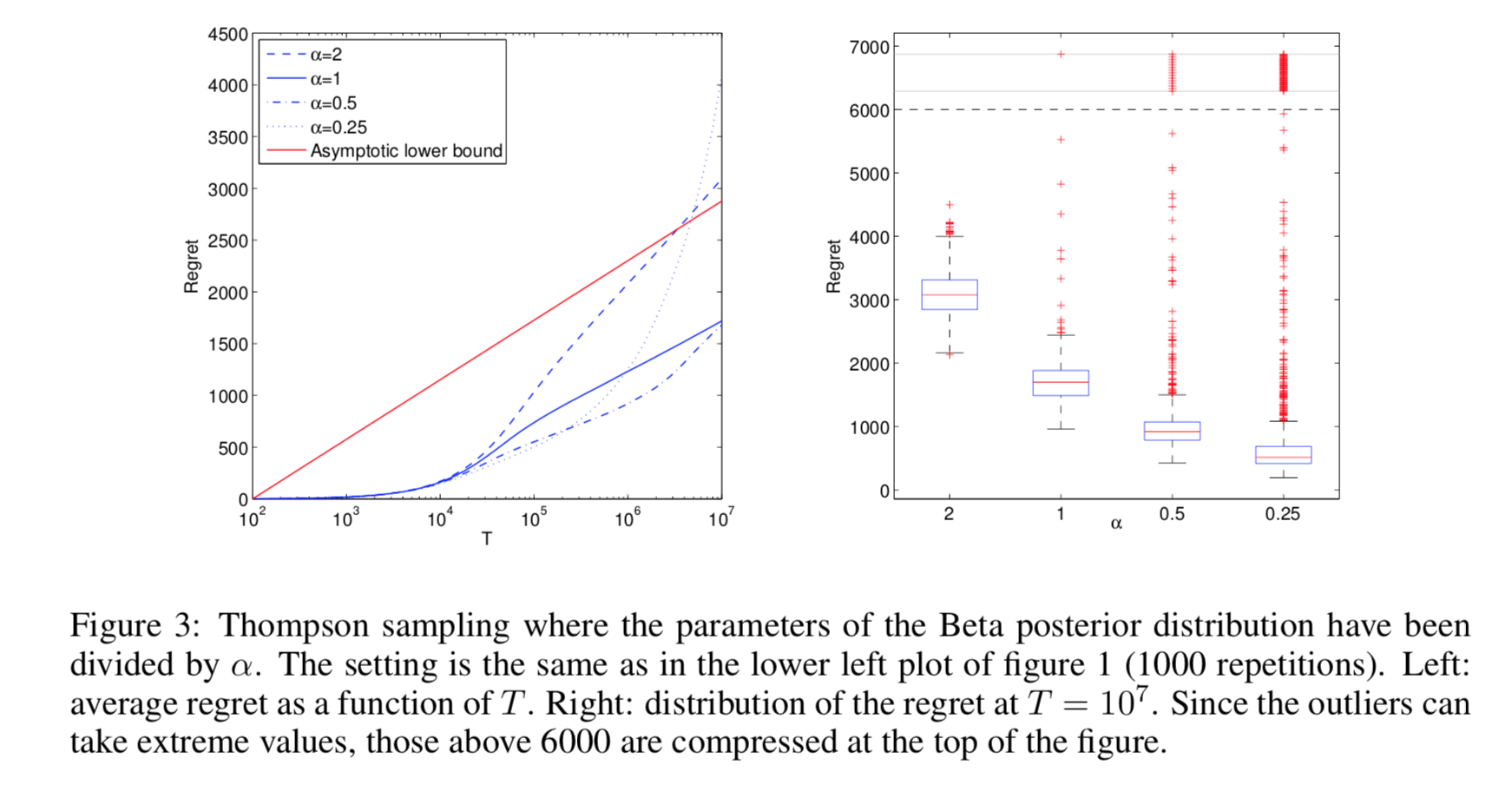
后验塑形: 改变后验分布,增加探索能力。例如把beta分布的a和b两个参数都除以$(\alpha)$,将在不改变期望的情况下增加方差,从而增加探索能力。
- 试验结果显示,虽然在渐进区域(T很大的区域)改变后验分布反而使得regret比标准版的TS效果要差,但是在非渐进区域,可以得到更好的regret的。
- 启示: 可以在早期的时候将$(\alpha)$设置为小于1,减少探索性,加快收敛,在后期的时候逐步增加到1

后验塑形

时延的影响: 因为实际系统中,反馈往往存在时延。作者通过一个模拟仿真,证实汤普森采样比UCB在时延变长的时候更加鲁棒。(ratio指的是UCB的regret/汤普森采样的regret,该值越大,说明ts比ucb越好)

时延的影响

假设模型参数的先验分布, 以正则化逻辑回归为例,假设参数先验为高斯分布
后验分布并不是高斯分布,所以采用拉普拉斯近似,将众数作为高斯的均值,二阶导作为协方差矩阵(只取了对角项,没有要交叉项)
拉普拉斯近似具体操作过程可以参考PRML
仿真的结论是, TS比UCB和e-greedy都要好,但是没有探索的方法效果也不差! 作者认为一个可能的解释是, 不同的上下文本身有带有一定的探索。
BOPR: BOPR则将概率函数直接用高斯分布的类似形式,都不用近似。参考: Web-scale Bayesian click-through rate prediction for sponsored search advertising in Microsoft’s Bing search engine

汤普森采样LR