Table of Contents
关于
- 收集一下近期推荐系统相关的一些热点文章,及其相关的论文。
在此基础上,做简要阅读和评论,重点精读的文章单独写一篇笔记。
论文
NCF vs MF
- 论文:Neural Collaborative Filtering vs. Matrix Factorization Revisited
- 作者 Steffen Rendle 是 FM 的发明人,绝对大佬
- 知乎讨论https://www.zhihu.com/question/396722911
主要观点
- 比较了基于矩阵分解的方法和目前基于MLP的NCF方法,
指出在合适的超参数选择下,矩阵分解的方法比NCF更好 - 虽然MLP可以近似任意函数,但是作者证实他确很难学到点积!
很难学到的意思是,需要很高的模型容量以及很多数据才能学到 - MLP太慢了,不如点积,因为点击可以用近似索引
- 作者不是说MLP不好,而是希望不要被MLP能近似任意函数误导,
MLP需要较大数据和较低emb维度,才能拟合得好相似函数
详细内容
- 两种学习相似函数的模式,点积和MLP
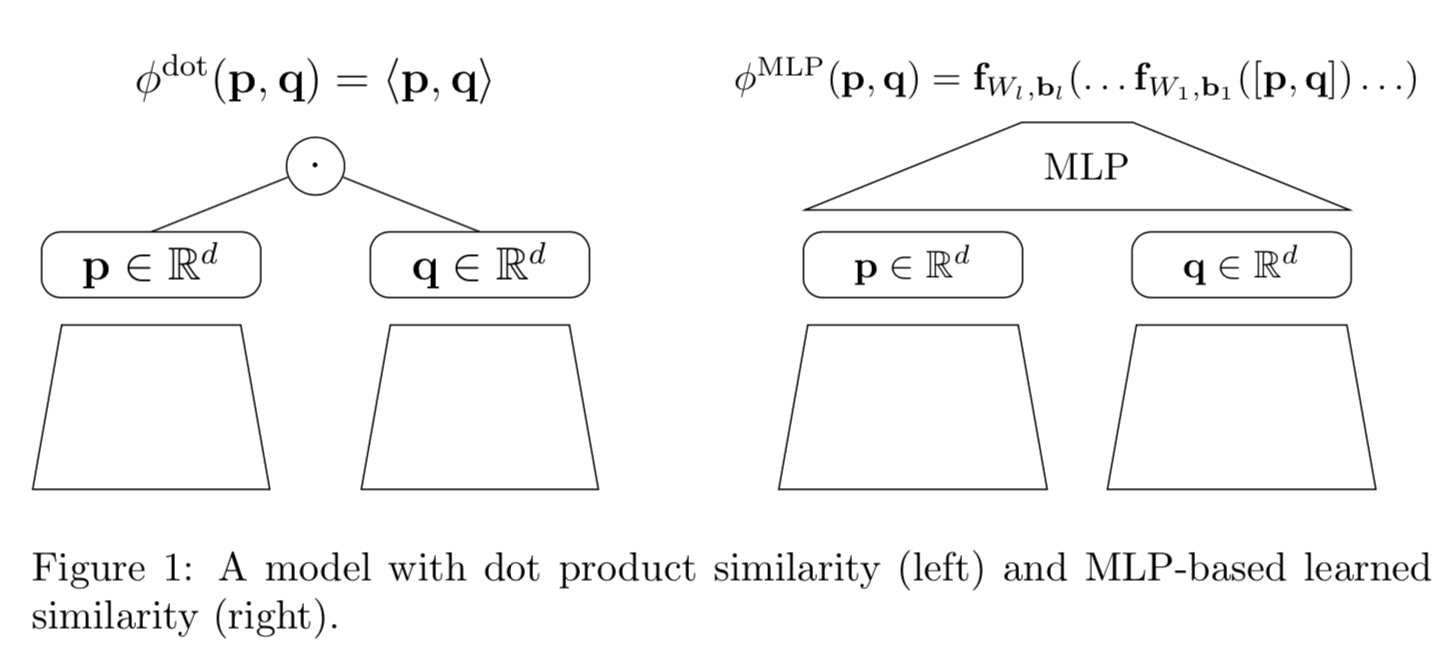
- NCF原始论文(2017)用MLP和GMF两个分数来表示相似(模型结构见下图),GMF是用加权的内积
$$
\phi^{GMF}(p, q) = \sigma(w^T(p \bigodot q))
$$
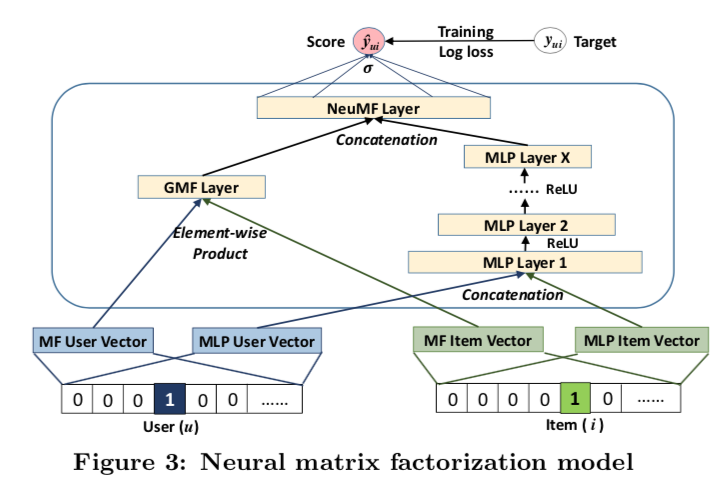
-
NCF原始论文里面,GMF没有对权重w正则,是导致不稳定的因素。
因为p和q有正则,会导致p和q倾向于减小,如果w同时增大对应的倍率,
那么损失函数实际上不变。另外,w的信息实际上可以让p和q来学到,
所以增加w这个参数实际上并没有增加模型容量。 -
MLP难拟合内积,误差界是 $( O(d^4/\epsilon^2) )$
- 上述误差界来自于论文, Learning Polynomials with Neural Networks,
这篇论文的主要结论见后文 - 试验评估指标:hit rate(即召回率),NDCG
评论
- MLP难以学到点积这个点比较有意义,这是不是说明了在DNN时代,
手动做一些交叉还是能拿到一些收益的?例如,W&D中用wide来记忆
用户历史行为跟item的交叉。在DeepFM中用FM来交叉emb向量,对于更上层的
向量,实际上也可以发现对他们做交叉也能有一些收益。 - 虽然GMF那种方式没有增加模型容量,但是如果将元素乘法的向量放到MLP里面,
还是能增加模型容量的。并且多了显式交叉的信息。 - 实际上目前工业界是拿点积做召回(如DSSM),MLP用来做精排,点积确实快,
但是限制了模型容量 - 召回的模型评估指标:hit rate,MRR,NDCG 都可以,hit rate侧重召回率,
后两个侧重排序。 - 论文提到用MLP学习内积比较难,但是为什么要学习内积呢?逻辑上不是太通
- 用MLP来拟合内积的代码,作者给的链接好像打不开。我实现了一个demo,用MLP来拟合内积,见 https://github.com/tracholar/ml-homework-cz/blob/master/mlp-dot/tracholar/mlp_dot.py
NN学习多项式
- Learning Polynomials with Neural Networks,2014
- 本文是一篇偏理论的文章,主要是在上一篇论文中提到的一个结论,
但是我认为这篇文章里面的一些结论,对设计网络的人来说,
还有有一些启发价值的。
主要结论
- 任何多项式都可以通过线性组合随机初始化的充分多个神经元,来任意逼近。
也就是说,含有一层隐层的MLP可以拟合任何多项式。神经元的个数需要$(O(n^{2d})),
n是输入变量个数,即输入的维度。
Representation Theorem
- 简单表述:在一个有限的范围内,可以用指数函数任意逼近d阶多项式。
在逼近误差为$(\epsilon)$的时候,需要$(m = O(n^{2d}/\epsilon^2))$个神经元。
用梯度下降优化
- 用隐层数目为$(m = O(n^{2d}/\epsilon^2))$的单隐层神经网络,可以通过随机初始化权重
的方式(权重的范数为$(1/\sqrt{n})$),学习率 $(\lambda < 1/m)$,那么用梯度下降优化,
将可以通过$( O(\frac{n^{2d}}{\lambda \epsilon^2 m}) )$步迭代,收敛到误差$(\epsilon)$以内。
LightGCN
- 论文:Xiangnan He, Kuan Deng ,Xiang Wang, Yan Li, Yongdong Zhang, Meng Wang(2020). LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation
- NCF作者 Xiangnan He 的新作
- GCN现在也很火
主要观点
- 在user-item交互图上做GCN,只保留推荐有价值的邻居聚合,
通过试验证实GCN的特征变换跟非线性激活函数对CF意义不大,
可以去掉,所以叫做lightGCN - 聚合方式如下公式所述,邻居部分,用了邻居节点向量,
还有跟中心节点的元素乘法交叉后的向量。看起来大家都喜欢用显式交叉。
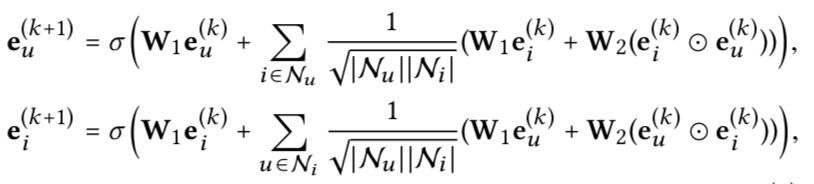
- 最终的用户向量跟item向量是多层GCN的向量的concat,类似于DENSE net
- 作者认为上述操作中的激活函数,跟两个权重W可以去掉。但是前提是,
原始输入是id embedding特征,但是如果是一些内容特征,这个变换还是有必要的。 - 发现移除上述两个操作后,效果更好,见下图
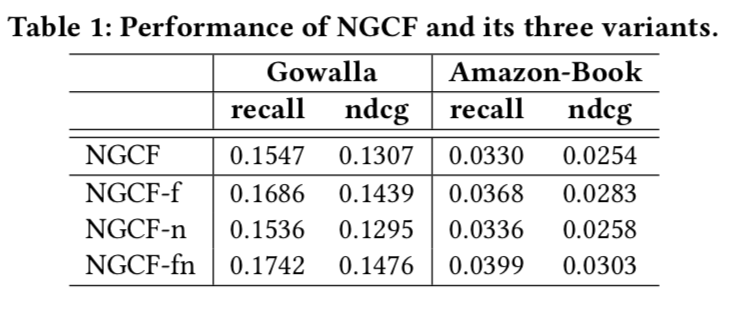
- 另外,最终的向量将多个GCN抽取的向量求和,而不是concat
- 作者提出的模型(即lightGCN):
- 聚合直接用邻居平均向量,权重取决于节点的度
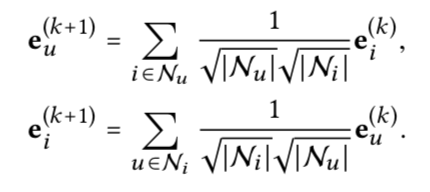
- 多个向量融合,不用concat,而直接用加权和
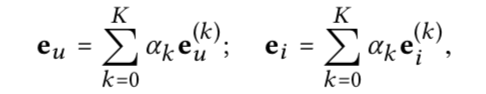
- 聚合直接用邻居平均向量,权重取决于节点的度
评论
- 这篇工作对落地挺有价值,告诉我们GCN中真正有价值的点其实是对邻居的加权聚合,
其实这个比较好理解,没有GCN的时候,推荐模型中也会有特征变化等操作,但是没有
图结构信息,这个信息正是邻居聚合操作所带来的新信息。 - 邻居聚合中的跟邻居元素乘法的交叉项,在U-I图中是有业务意义的,
它代表用户跟item的交互,推荐模型本质上就是为了学这些交叉,
这里直接手动交叉了,省得用MLP去学了,毕竟前面论文也提到,
MLP学内积还挺困难的。 - 将每层GCN学到的向量concat,实际上类似于学到不同尺度的特征,
都应用到最终的结果中。 - 为什么id类特征不用再做变换,因为它本身的参数就是学出来的,
所以再学一下变化,实际上有点多此一举了。但是,如果本身特征不是
学出来的,而是item的标题等特征emb向量,那么还是有必要的。 - 这篇文章的一个启示是,做推荐模型的时候,不必要的结构还是不要加进去,
毕竟加容易,下线就难了,如果没多大用,还浪费资源。另外,如果有先验知识
就不要让模型自己去学了,实际上最后将多层做concat然后放到MLP中,就是
希望让模型自己学一些变换,而作者直接用加权和,这个当然得看数据量了,
数据量不够的时候,这种方式更好些。
多任务多物料推荐
- 论文:M2GRL: A Multi-task Multi-view Graph Representation Learning Framework for Web-scale Recommender Systems
- 阿里的作品,有线上试验
主要观点
- multi-view data实际上是指辅助信息,现有的方法都可以看做
multi-view representation fusion。即先构造一个图,
然后将其他辅助信息融合到节点的表达中。 - 这种方法存在的工程问题:multi-view data很多,可能用单个向量难以表示。
不同view的数据的分布差异很大。可以用本文提出的 multi-view representation alignment
解决。 - 每个view创建一个图,然后将每个图的向量对齐。如下图所示,用户行为序列可以拆成
shop序列,item序列,category序列。每个序列都是一个view。
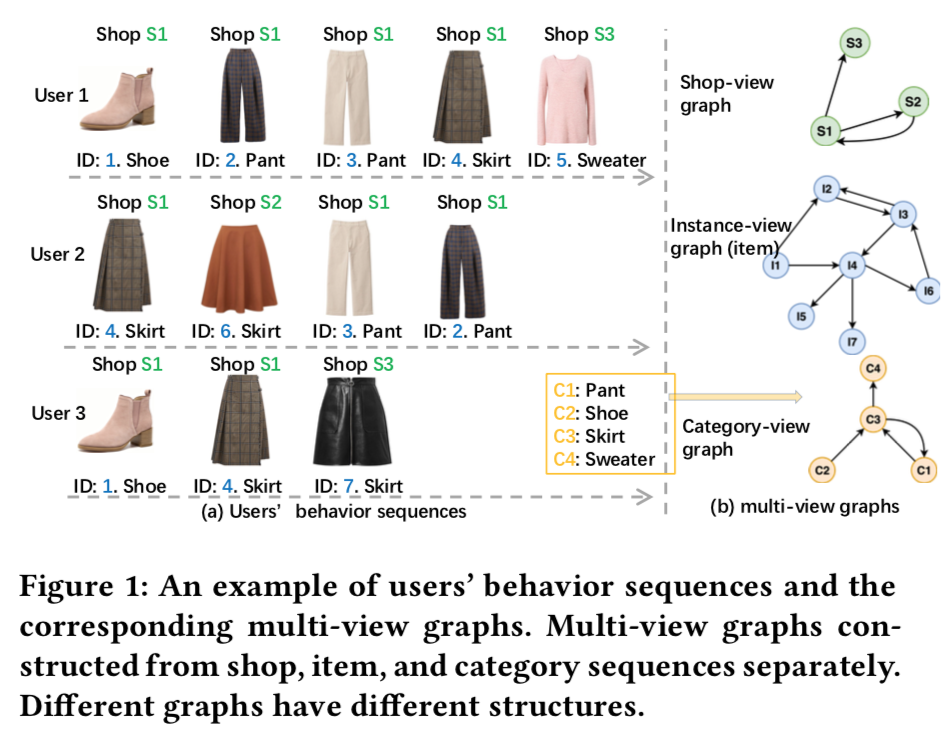
- 图构造的一些细节
- 数据清洗:过滤掉浏览时间少于2秒的
- session分割合并:用1小时gap来分割session;如果两个session的gap小于30分钟,
合并成一个session。
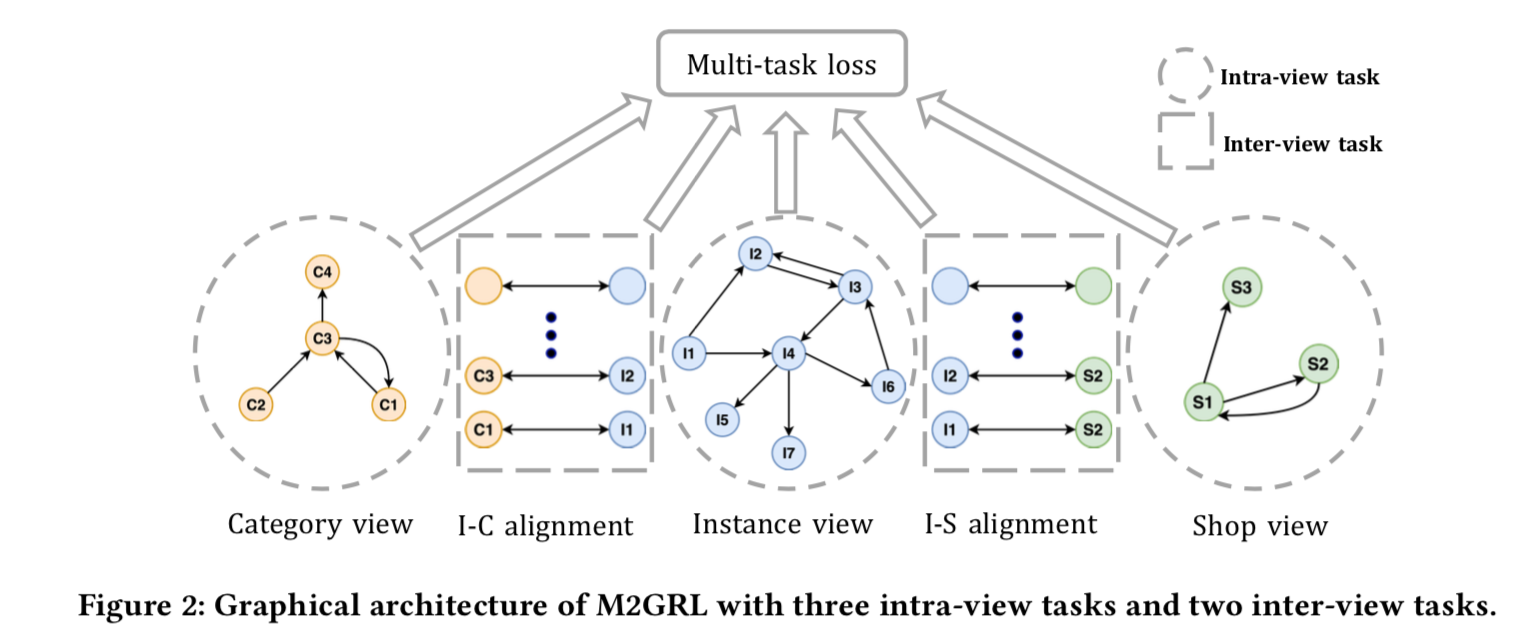
-
multi view align:
- 2个对齐:instance - category (I-C) and instance - shop (I-S))
- 利用item跟品类的关系对齐,如果i的品类是c,那么得到一个关系(i, c)用于对齐
- 对齐损失,在对齐集合中要求内积很大,不在对齐集合中要求内积负的很大。
$(\sigma)$是sigmoid函数,用于归一化。W是对齐矩阵。
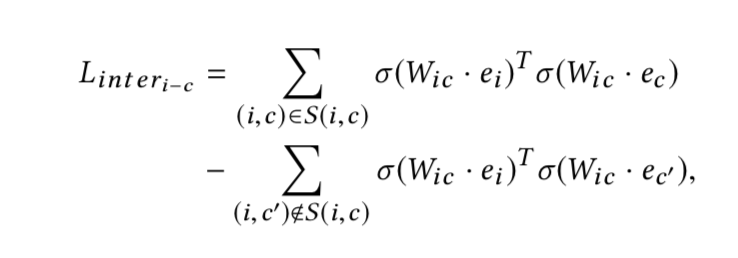
-
最终的损失是对齐损失与负采样损失的加权和,让emb向量同时学到view内的相似与view间的对齐。
- 推荐任务:利用instance view的向量,做相似度检索,item2item
- 多样化推荐:
评论
- 感觉跟将多个辅助信息embedding加到item向量中,没什么本质区别;
不是太能理解收益的来源
Embedding压缩
- 论文:Res-embedding for Deep Learning Based Click-Through Rate Prediction Modeling
- 利用残差编码的方式,压缩emb
- 阿里盖坤出品,里面的结论有较大借鉴价值
主要观点
- 大家都在改非线性映射部分(MLP部分),很少人去搞emb部分
- 在理论上证明了:神经网络 CTR 模型的泛化误差与 Item 在 Embedding
空间的分布密切相关,如果用户兴趣相近的各 Item,在 Embedding 空间中的
envelope 半径越小,也就是说,相同兴趣 Item 之间在 embedding 空间中越紧致,
形成的簇半径越小,则模型泛化误差越小,也就是模型的泛化能力越好。 - emb部分非常影响模型的泛化能力,不同的初始化将导致两个item的距离差异很大
- 用户点击序列可以看做是从兴趣序列中采样而来,整个生成过程可以看做一个HMM
- 用户兴趣向量是z,兴趣序列 $( (z_1, z_2, ..., z_T) )$
- 用户点击行为x是在z兴趣下的一个采样,采样分布是 P(x|z),这个点的意义
在于,同一个兴趣z下,x的分布应该是紧密的(x的分布比较集中)
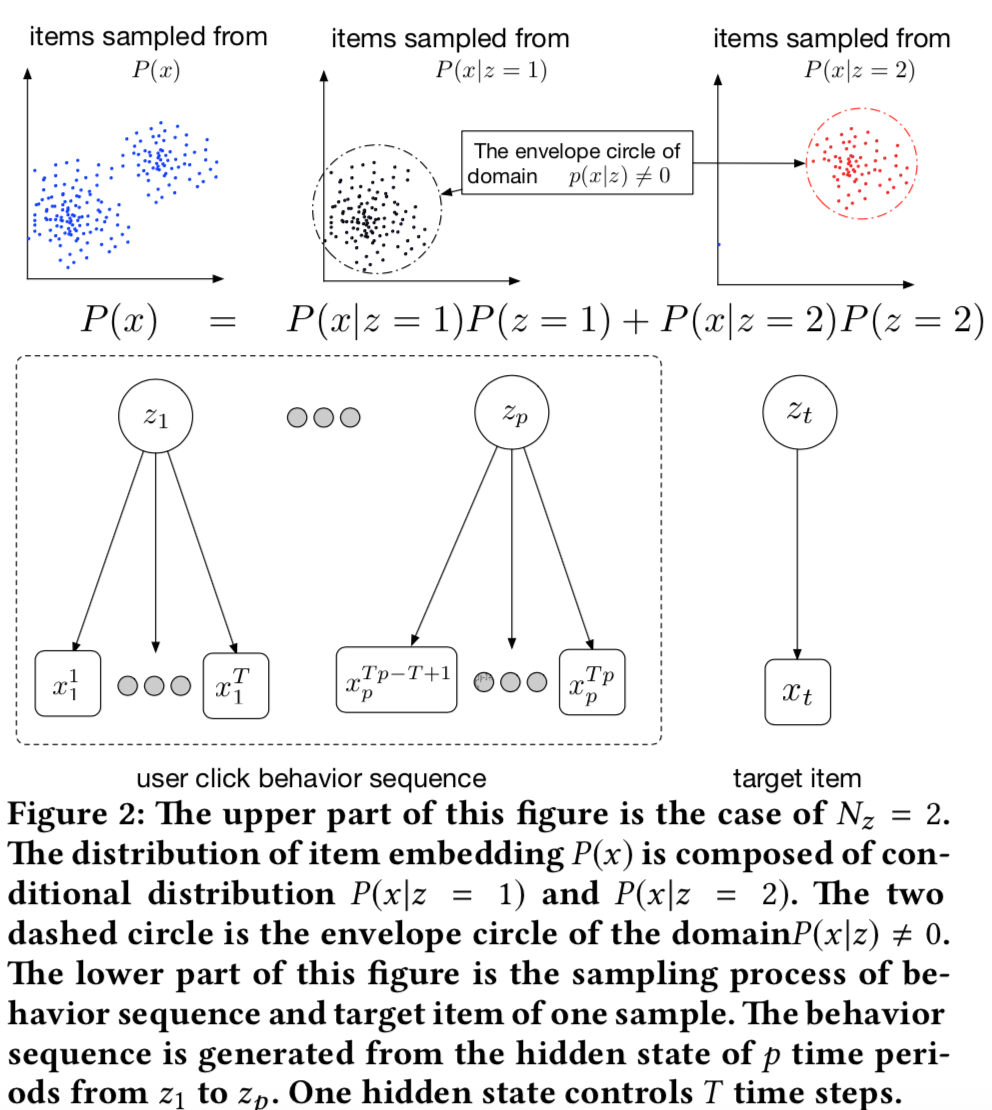
- 误差界,理论比较复杂,主要结论是,泛化误差跟emb向量的模长、
emb向量的每个兴趣内的半径 正相关。控制模长会影响模型容量,
但是改变emb向量的分布可以在不影响模型容量情况下提升效果。

-
item向量分解为中心向量+残差向量,通过限制残差向量的模长,
可以实现减少半径的效果。$(W \in R^{H\times I})$ 是兴趣投影矩阵。
$( C \in R^{I\times d} )$ 是每个兴趣中心emb向量。$( R \in R^{H\times d} )$是残差向量。
$$
E = WC + R
$$ -
session图的构造方法是,在session内用滑动窗来构造,用总的共现次数作为权重,
得到链接矩阵Z。W = g(Z),g可以选择不同的函数,用来表示转移关系。g可以有以下选择,
试验结果表明,GCN跟ATT做法差不多,但是GCN更简单,因为他就是用顶点的度加权,
而且有明确的意义,一个item A跟很多item共现,那说明A对某个共现的item C的影响比较小,
但是item B只跟C共现,那么B跟C是强相关的!- 用平均值,即item向量是共现的item的平均
- 用GCN的做法,即用顶点的度做归一化
$$
g(Z) = D^{-1/2} Z D^{-1/2}
$$ - ATT做法
评论
- 本质上,是希望将相同兴趣的emb向量映射到相近的空间。在现有的推荐模型中,
用户行为序列中的emb是没有一种方式来施加这种约束的。这种约束大约有几种
施加的方式,一种是像本文一样,在emb向量中让相似的item共享一部分emb,
也有把item向量分为品类+残差的方式。令一类是施加某种损失约束,让item相似。
比如,是否可以将session内的item构造个负采样损失函数,加到目标函数中,
作为辅助损失,这样不就可以实现本文的目的了吗。 - 另外想到一个点,GCN层可以看做一种基于图结构的变换,那么对emb向量X有
$( X_{t+1} = F_{GCN}(X_t) )$,如果高很多相同的层,那么X实际上
是这个变换(假设参数相同)的不动点!如果变换还是线性的话,那么X还是
这个线性变换的特征向量!