Rerank机制调研

问题

• 现有的推荐模型基本上都是预测一个得分f(u, i)，是一个pointwise模型。而实际上排序时，对i的打分还依赖前后的item，所以应该是listwise模型。rerank就是为了解决这个问题

传统方法

• 在排序中，可以利用lambdaMart，优化list的损失函数来实现

微软2009

• Diversifying Search Results
• 基本思路是在排序得到一个文档集合之后，先初始化一个空集，然后贪心地将边际收益最大的文档加入集合中
• 边际收益的定义。假设有很多个类别，query和document都有一定概率属于某个类别。用$( V(d| q, c) )$ 表示在query为q，类别c的条件下，出文档d的价值（比如相关性）；用$( U(c | q, S) )$ 表示在集合S都不属于c类别条件下，q属于类别c的概率。那么在列表S中加入文档d带来的边际收益（额外增加的价值）可以表示为：现有的S都不是c类别但query的意图是c类别，此时文档d带来的收益为V(d|q,c)。对所有类别求期望有
  $$
  g(d|q, c,S) = \sum_{c \in C(d)} U(c|q,S) V(d|q,c)
  $$
  C(d)是文档d的所属类别集合（文档可以属于多个类别）。
• 当在集合S中增加文档d后，条件概率$(U(c | q, S \cup {d}))$的更新表达式为
  $$
  U(c|q, S \cup {d}) = (1 - V(d|q,c))U(c | q, S)
  $$

多臂老虎机-ICML2008

- Learning diverse rankings with multi-armed bandits

MMR

• The use of mmr, diversity-based reranking for reordering documents and producing summaries
• 最大化边际相关性
• 对于给定的文档集合S，往里面加一个新的文档d的边际相关性为
  $$
  \lambda Sim_1(d, q) - (1-\lambda) \max_{d_i \in S} Sim_2(d, d_i)
  $$
  即为文档d与q的相关性减掉d与S中所有文档中最大相关性！

xQuAD

• 预定义效用函数，对相关性和多样性加权，多样性的衡量是改写的qi和现有集合S中的文档都不相关但与文档d相关的概率。
  $$
  (1-\lambda P(d|q)) + \lambda \sum_{q_i \in Q}P(q_i|q)P(d|q_i) \Pi_{d_j \in S} (1-P(d_j|q_i))
  $$

SVMDiv

多样性

• Learning for search result diversification

MDP-2017

• Adapting markov decision process for search result diversification

优化整个页面的rank

• Beyond ranking: Optimizing whole-page presentation

阿里：Globally Rank

• Globally Optimized Mutual Influence Aware Ranking in E-Commerce Search
• 将问题建模为估计$(p(i|c(o, i)))$ c是上下文中的item，上下文是指排序展示结果中有的item
• 关键是构造global特征，global特征构造方法是算一个全局分位点值
  $$
  f' = \frac{f - f_{min}}{f_{max} - f_{min}}
  $$
• 最后将rerank建模成一个序列生成模型，用RNN来做decoder，用beam search来做搜索
• lambdaMART用了listwise的损失函数，但是模型没有使用展示的list中的信息，这里的一个创新点应该是还利用到了list中的信息来做特征，建模这个得分。

阿里：个性化rerank

• Personalized Re-ranking for Recommendation
  

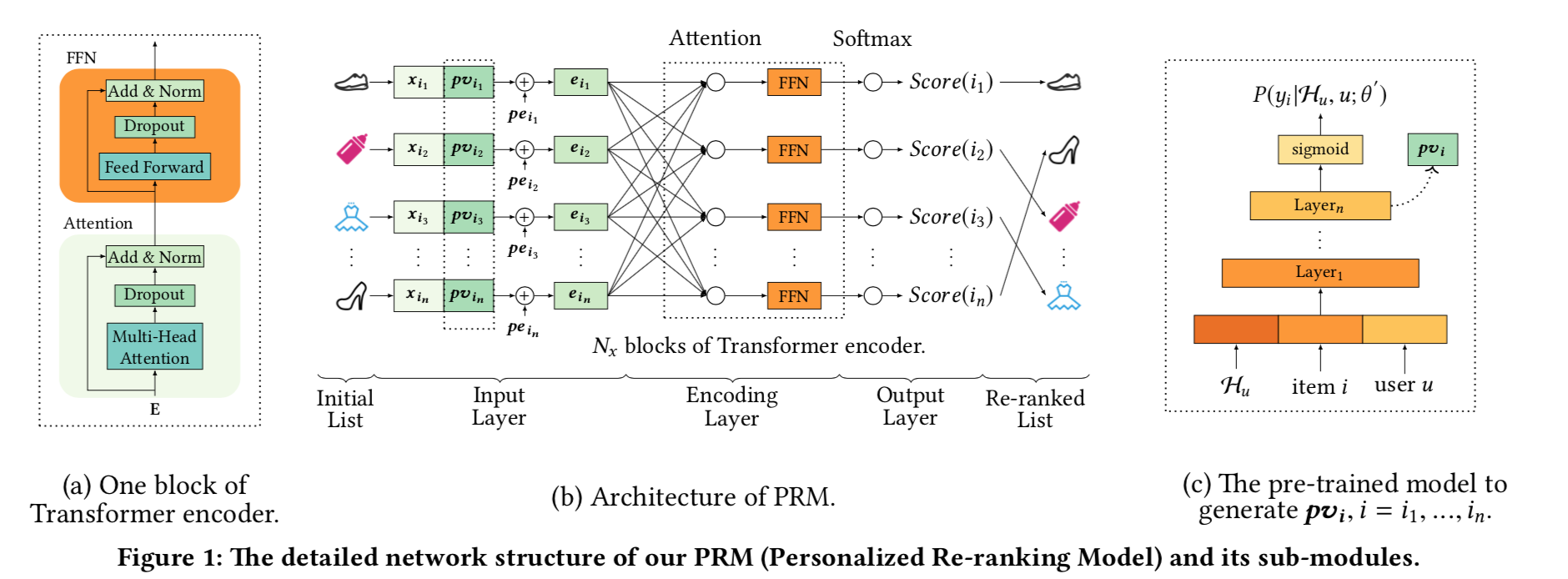
• recsys2019年，阿里发表的文章

• 将问题建模为对排序后的每一个item计算一个得分 $(P(y_i | X, PV; \theta))$，其中X是该list所有item的特征矩阵，PV是一个正常pointwise排序模型（比如W&D）最后一个隐层输出向量，作为用户和这个item的个性向量
• 本质上是建模一个序列(排序后的item列表)到另一个序列(每一个item的打分序列)的问题
• 将item特征向量和pv向量拼接，在加上position Encoder向量，通过一个transformer来建模这个序列到序列的变换模型；最后一层是一个softmax，监督信号是点击之类的信号

DPP：行列式点过程

• 参考 http://people.csail.mit.edu/stefje/fall15/notes_lecture21.pdf
• Determinantal Point Processes for Machine Learning http://www.alexkulesza.com/pubs/dpps_fnt12.pdf

行列式点过程

• 一个点过程P是行列式点过程是指，如果Y是一个采样自P的随机子集，那么对任意 $(S \subset Y)$，有
  $$
  P(S \subset Y) = \det(K_S)
  $$
  其中$(K)$是一个实对称半正点相似矩阵，$(K_S)$代表子集S作为下标集合表示的子矩阵。
• 由于K的任意子矩阵的行列式表示一个概率所以，K的特征值应该都在[0,1]区间，因此有$(0 \le K \le 1)$
• $(P(e_i \in Y)= K_{ii})$
• $(P(e_i, e_j \in Y)= K_{ii}K_{jj} - K_{ij}^2 = P(e_i \in Y) P(e_j \in Y) - K_{ij}^2)$，也就是两个元素同时出现的概率小于分别出现概率的乘积！！这表明这两个元素是互斥的！Kij越大，表示这两个元素同时出现的概率越小！
• 如果 $(K_{ij} = \sqrt{K_{ii} K_{jj}})$ 表示i和j是完全相似的，这两个item同时出现的概率接近于0！
• 当没有交叉项，也就没有斥力项，此时K是对角阵，不同元素之间互相独立！

例子

• https://arxiv.org/pdf/0904.3740.pdf
• 长度为N的序列，每个元素是从集合I中选出，从这个序列的第二个元素开始，如果当前元素小于前面一个数，那么就把这个元素的下标选出，这些下标的分布构成一个行列式点过程。

L-ensembles

• 对一个实对称阵L，点过程 $(Y \subset V)$ 的未归一化概率为
  $$
  P_L(Y) \propto \det(L_Y)
  $$
• 如何计算归一化常数。有下列定理(⚠️)
• 对任意$(A \subset V)$
  $$
  \sum_{A \subset Y \subset V} \det(L_Y) = \det(L + I_{\bar{A}})
  $$
  其中$(I_{\bar{A}})$ 是一个对角阵，A中下标对应的对角元素是0，非A中的下标对角元为1.
• 当 $(A = \phi)$空集时，就得到L-ensembles的归一化常数为
  $$
  \sum_{S \subset V} \det(L_S) = \det(L + I_V)
  $$
• 用核矩阵（归一化的）K和实对称阵L定义DPP是等价的，并且这两个矩阵有关系
  $$
  K = L(L + I)^{-1} = I - (L + I)^{-1} \\
  L = (I - K)^{-1} - I = K (I - K)^{-1}
  $$
• 特征值分解，如果L的特征值分解为 $(L = \sum_k \lambda_k v_k v_k^T)$，那么$(K = \sum_k \frac{\lambda_k}{\lambda_k + 1} v_k v_k^T)$
• 几何视角：点过程$(x_1,...,x_n)$是n维空间中的点过程，那么可以构造矩阵$(L_{ij} = x_i^T x_j)$，那么 ⚠️
  $$
  P_L(S) \propto \det(L_S) = Vol^2(\{x_i\}_{i \in S})
  $$
  如果一个集合包含的点具有更多的多样性，那么体积也就越大，所以概率也就越大。

DPP的应用

• 尽管DPP的可能子集数目是指数规模$(2^N)$，但是DPP的很多概率推断却可以在多项式时间复杂度完成！
• 如果$( Y \sim DPP(K) )$，那么Y的补集 $( \bar{Y} \sim DPP(I - K) )$ ⚠️
  $$
  P(A \cap Y = \phi) = \det(I - K_A)
  $$
• 其他略，参考原始材料吧
• DPP众数，找到一个集合Y，最大化概率$(P_L(Y))$是一个NP-hard问题

DPP采样

• 问题：
  • 如何采样
  • 样本中有多少个点
• element DPP：如果核矩阵的特征值为{0,1}。一个DPP可以看做多个基础DPP的混合！
• 定理：一个DPP，$(L = \sum_k \lambda_k v_k v_k^T)$ 可以看做多个基础的DPP的混合：$(P_L = \frac{1}{\det(L + I)} \sum_{T \subset U} \Pi_{k\in T} \lambda_k P^T)$

Google YouTube

• Practical Diversified Recommendations on YouTube with Determinantal Point Processes
• rerank的目标，最大化总交互数目
  $$
  G' = \sum_{u \sim user} \sum_{i \sim item} y_{ui}
  $$
• 为了刻画rerank的收益，rerank的目标是把交互的用户和item对排到最前面，可以用下述累积收益来刻画
  $$
  G = \sum_{u \sim user} \sum_{i \sim item} \frac{y_{ui} }{j}
  $$
  j 是rerank后的排序！上述收益可以刻画rerank的排序效果！
• 两个item是相似的，如果他们放在一起会导致效用下降
  $$
  P(y_i=1, y_j=1) < P(y_i=1)P(y_j=1)
  $$
  如果feed流中有两个item是相似的，那么排序策略不是最优策略了！

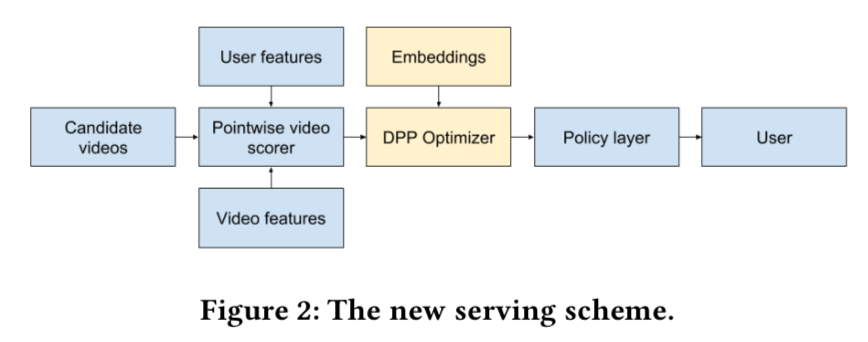
• 有N个item，用0表示用户没有点，1表示点击，那么N个item对应的用户的行为向量为[0,..,1,..,0]，其中点击的下标服从行列式点过程！！因为下标是「当前元素小于前一个数」（假设1小于0），所以刚好是DPP中的那个例子！

• 因此用户点击的item下标服从DPP，点击下标集合Y的概率分布可以用一个矩阵的行列式来表示
  $$
  P(Y) = \frac{\det(L_Y)}{\sum_{Y ' \subset S} \det(L_{Y'})}
  $$
  S = {1,2,3,...,N}是全量下标集合。上式的分母可以简化为
  $$
  \sum_{Y ' \subset S} \det(L_{Y'}) = \det(L + I)
  $$

• DPP核矩阵的定义，假设第i个video的Pointwise得分为$(q_i)$，sparse embedding向量为$(\phi_i)$。假设排序完有N个video，定义如下核矩阵
  $$
  L_{ii} = q_i^2 \\
  L_{ij} = \alpha q_i q_j \exp(- \frac{D_{ij}}{2\sigma^2}), i \neq j
  $$
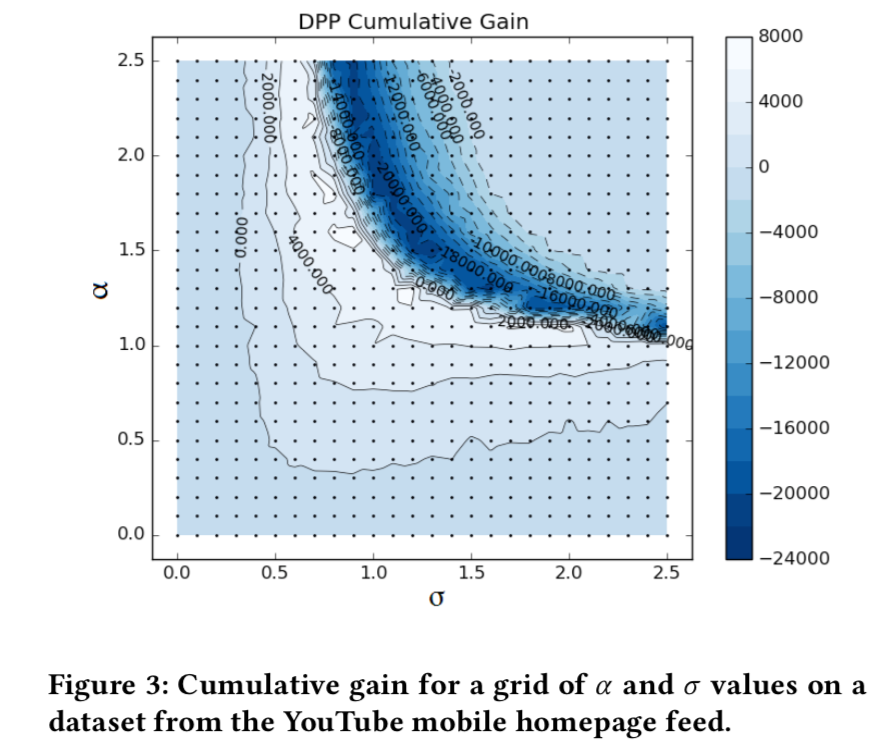
  $(D_{ij})$是i和j的距离，通过embedding向量计算得到。

• 当$(\alpha)$较大的时候，代表斥力很大，但是就无法保证核矩阵的半正定要求。作者通过一个投影操作，将核矩阵强行半正定化。投影的方法是，将核矩阵对角化，然后将负特征值强行置0！
• 训练方法
  • 数据偏差，通过ee来实现
  • 超参数$(\alpha, \sigma)$ 通过gridsearch来寻找

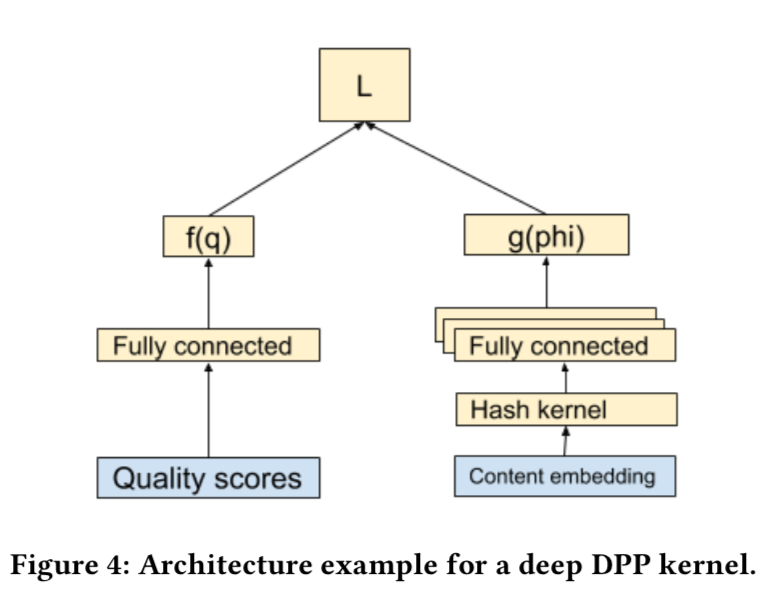
Deep Gramian Kernels

• 启发式的核矩阵，不容易分布式
• 直接用模型学习kernel矩阵
• 核矩阵的参数L有r个参数，用向量w表示。$(L = L(w))$
• 训练集：
  1. 有N个items
  2. 用户有交互的item下标集合Y
• 优化目标：极大似然估计出参数w，拟合实际的观测样本Y
  $$
  loglike(w) = \sum_j \log P(Y_j|w) = \sum_j \left[ \log \det(L(w) _ {Y_j}) - \log \det(I + L(w) _ {Y_j}) \right]
  $$
• L的参数：item的embedding向量、质量分$(q_i)$向量（多个质量分维度，而不是最终的一个分数）
  $$
  L_{ij} = f(q_i)g(\phi_i)^T g(\phi_j)f(q_j) + \delta \mathbf{1}_{i=j}
  $$
  f和g是两个神经网络，f是标量，而g是一个向量，$(\delta)$是正则参数。这种方法可以保证L是半正定的，而不用投影！

Efficient Ranking Algorithm with DPP

• DPP layer接受到N个item的质量分q和video的embedding向量$(\phi)$
• 利用构造的方法或者神经网络的方法，计算出DPP的未归一化核矩阵L
• 选择固定的窗k << N，寻找最大概率的k个item，放到上面，然后依次执行该步骤，选出余下的item并排序。之所以要选择一个窗口，而不是对全部N个item来排序，是因为相似item的斥力随着展示距离而衰减！换句话说，距离达到一定程度后是可以放很相似的item的。N一般是几百，而k一般是10+的样子。
• 最大化k个item出现的概率对应下列优化问题，是一个NP-hard问题
  $$
  \max_{Y:|Y|=k} \det(L_Y)
  $$
• 这个问题可以通过贪心算法近似求解，即从一个空集开始，每次加入一个item都要使得现有的k个item对应的$(\det(L_Y) )$是最大的！

实验

实验对比：

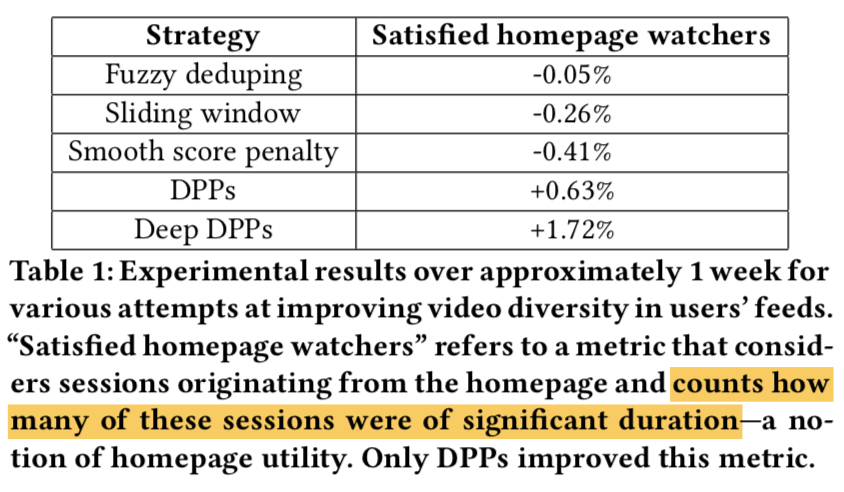
• Fuzzy deduping：从空集开始，贪心地增加item：新增加的item如果和现有集合中的item距离小于一个阈值就干掉！
• Sliding window：每m个item最多n个的距离可以小于一个阈值
• Smooth score penalty：将相似作为惩罚系数
  $$
  q_{new, v} = q_{origin,v} * e^{-b(\phi_v \cdot \phi_{prev})} \\
  \phi_{prev} = \sum_{k=0}^{n} a^{n-k-1} \phi_k
  $$
• 这些方法都没有正向效果。只有DPP和Deep DPP有正向效果
• 对稀疏向量，使用Jaccard 距离应用到item token比较有效
• 核参数版本的DPP有明显正向效果，首页满意观看指标+0.63%，观看时长+0.52%。已经部署到TV，桌面，Live stream等场景。
• Deep DPP虽然在第一个指标提升1.72%，但是由于对排序改动较大，对第二指标不利影响，仍需要继续调优！所以还没有部署。
• 长期学习效应：多样性带来更长期的收益，并且随着时间逐渐巩固！

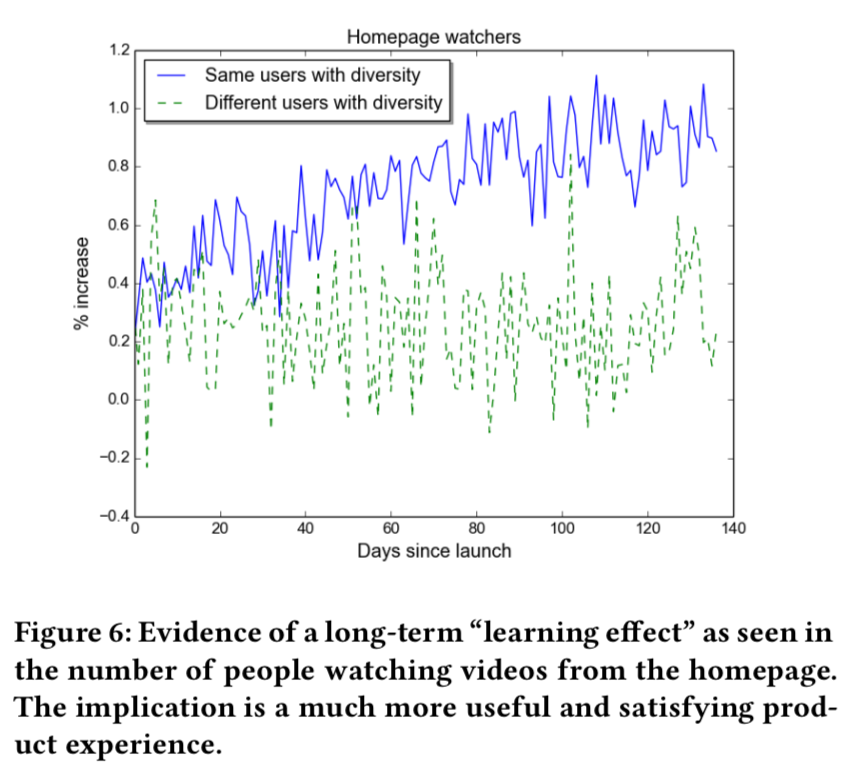
结论和未来规划

• 多样性具有短期和长期双重收益
• 当前的多样性策略没有考虑用户的个性化、item的类型可能影响多样化需求。以及时间因素
• 未来会利用强化学习探索多样性的调控策略

思考

• DPP相比于传统的多样性方法，本质区别是什么？传统的方法还是将多样性作为一个目标，而DPP确实在优化用户交互这个目标，多样性是为了这个目标所必需的。简单地说，传统的方法是在优化多样性本身，DPP是在优化用户对列表的总交互量！
• 个人的仿真实现代码：https://github.com/tracholar/ml-homework-cz/tree/master/dpp

created in 2019-11-05