关于
Bishop写得PRML无疑是机器学习领域的权威著作,是加强机器学习理论知识必看的书籍之一。
这里是我在阅读这本书时记录的笔记和自己的一些初步思考。
引言
曲线拟合
设曲线拟合的目标变量为$(t)$,$(N)$个训练集为
$( \mathbf{x} = (x_1, ..., x_N)^T )$,对应的目标值为
$( \mathbf{t} = (t_1, ..., t_N)^T )$。假设估计误差服从
高斯分布
$$
p(t|x, \mathbf{w}, \beta) = \mathcal{N} (t| y(x, \mathbf{w}), \beta^{-1})
$$
这里的$(\mathbf{w})$是待估计的参数,$(\beta^{-1})$对应于
估计误差的方差。此时,按照最大似然准则估计的参数就是最小二乘
法的结果,也就是最小化均方误差。而$(\beta^{-1})$的最大似然估计为
模型预测值与实际值的均方差。
$$
\frac{1}{\beta} = \frac{1}{N} \sum_{n=1}^N [y(x_n,\mathbf{w}_{ML}) - t_n]^2.
$$
如果我们对参数的具有一定先验知识,可以进一步采用最大后验概率估计,
得到更好的结果。作为一个特例,如果认为
$$
p(\mathbf{w}|\alpha) = \mathcal{N}(\mathbf{w} | 0, \alpha^{-1} \mathbf{I}) \\
= (\frac{\alpha}{2\pi})^{(M+1)/2} \exp(-\frac{\alpha}{2} \mathbf{w}^T \mathbf{w}).
$$
那么此时的最大后验概率估计为带$(L_2)$正则项的估计,
它最小化
$$
\frac{\beta}{2} \sum_{n=1}^N [y(x_n, \mathbf{w}) -t_n]^2 + \frac{\alpha}{2} \mathbf{w}^T \mathbf{w}
$$
也就是说正则项是对模型参数的一种先验知识,$(L_2)$正则项代表高斯先验。
那$(L_1)$代表laplace先验(待求证)?
第11章 采样方法
- 计算期望 $(E[f] = \int f(z)p(z) dz)$
- 通过采样一系列$(z_i ~ p(z))$ ,从而近似地用有限和来近似上述期望$(\hat{f} = \frac{1}{L}\sum_{l=1}^Lf(z_l))$
- 估计误差可以用上述统计量的方差来刻画
基本采样方法
- 一维分布变换关系 $(p(y) = p(z) \frac{dz}{dy})$
- 分布f(y)可以通过从[0,1]间均匀随机变量z,通过变换$(F^{-1}(z))$得到, F是y的累积分布函数
- 指数分布$(y = F^{-1}(z) = -\frac{1}{\lambda} ln(1-z))$
- 对于多维分布,通过雅克比矩阵 $(p(y_1, ..., y_M) = p(z_1, ..., z_M)|\frac{\partial(z_1,...,z_M)}{\partial(y_1,...,y_M)}|)$
- 高斯分布生成: Box-Muller方法
- $(z_1,z_2)$独立采样自服从(-1,1)之间的均匀分布
- 只保留在单位圆内的点,即满足$(z_1^2 + z_2^2 \le 1)$,从而得到单位圆内的均匀分布
- 构造新的变量$(y_1 = z_1(\frac{-2 ln r}{r^2})^{1/2}, y_2 = z_2 (\frac{-2 ln r}{r^2})^{1/2})$. 其中r是半径, 那么y1和y2就是两个独立的服从标准正太分布的随机变量
- 假设两个随机变量z1,z2服从正太分布,那么对应的极坐标r和$(\theta)$对应的分布是 $(r e^{-\frac{r^2}{2}})$ 和 $(\frac{1}{2\pi})$的均匀分布。显然这两个分布可以通过均匀分布通过逆变换的方法容易得到。
$$
r = \sqrt{-2 ln U_1} \\
\theta = 2\pi U_2
$$
如果是从单位圆内的变换过来,那么容易验证对应的$(\theta)$即满足第二个均匀分布,而半径s分布为$(2s)$,所以根据概率恒等关系有
$$
2s ds = r e^{-\frac{r^2}{2}} dr
$$
解这个微分方程可得 $(r = \sqrt{ln s} )$, 同时$(cos(\theta) = x/s, sin(\theta) = y/s)$,于是有
$$
z_1 = r cos(\theta) = x \sqrt{ln s}/s, \\
z_2 = r sin(\theta) = y \sqrt{ln s}/s
$$
- 一般的高斯分布$(\mu, \Sigma)$,将协方差矩阵分解为$(LL^T)$,那么对独立的标准正太分布向量z,做变换$(\mu + L z)$ 即可得到目标分布
def urnd(): return random.random() def exp_rnd(lb): assert lb > 0 x = urnd() return -1/lb*log(1-x) def gaussian_rnd(): r = sqrt(- 2 * log(urnd())) theta = 2*pi*urnd() return r * cos(theta) def cauchy_rnd(): z = (urnd()-0.5) * pi return tan(z) def cauchy_rnd2(): x = gaussian_rnd() y = gaussian_rnd() if y == 0.0: return cauchy_rnd() return x/y
- cauchy分布 $(p(x) = \frac{1}{\pi} \frac{1}{1+x^2})$
- 通过逆变换方法, z采样自U(0,1), 逆变换为 tan((z-0.5)*pi)
- 构造两个标准正态分布X,Y,那么X/Y 则服从cauchy分布
- 对第2点的证明, 做变量代换t=X/Y, 那么P(t_0<X/Y<t_0+dt)的概率微元为
$$
P(t_0)dt = \iint_{t_0<X/Y<t_0+dt} p_X(x)p_Y(y)dxdy \\
= dt \int_{-\infty}^{\infty} dy |y| p_X(t_0y)p_Y(y) \text{(积分变换)} \\
= dt \int_{-\infty}^{\infty} dy \frac{1}{2\pi} |y|e^{-\frac{1}{2}(t_0^2+1) y^2} \\
= \frac{1}{\pi} \frac{1}{1+t_0^2} dt
$$
拒绝采样
- 目标分布p(z)不简单(比如没有解析表达式,或者有但是逆变换很困难etc),但是p(z)对给定的z还是要容易算出来
- 对于已有的某种分布q(z),选取足够大的k使得$(kq(z) \le p(z))$
- 每次采样的时候,首选从q中采样一个z,然后随机一个(0, kq(z))均匀分布u,如果$(u>p(z))$则拒绝该样本,否则就得到目标分布的一个采样。容易验证这样采出来的z分布为 $(q(z) \times p(z)/kq(z) = p(z))$
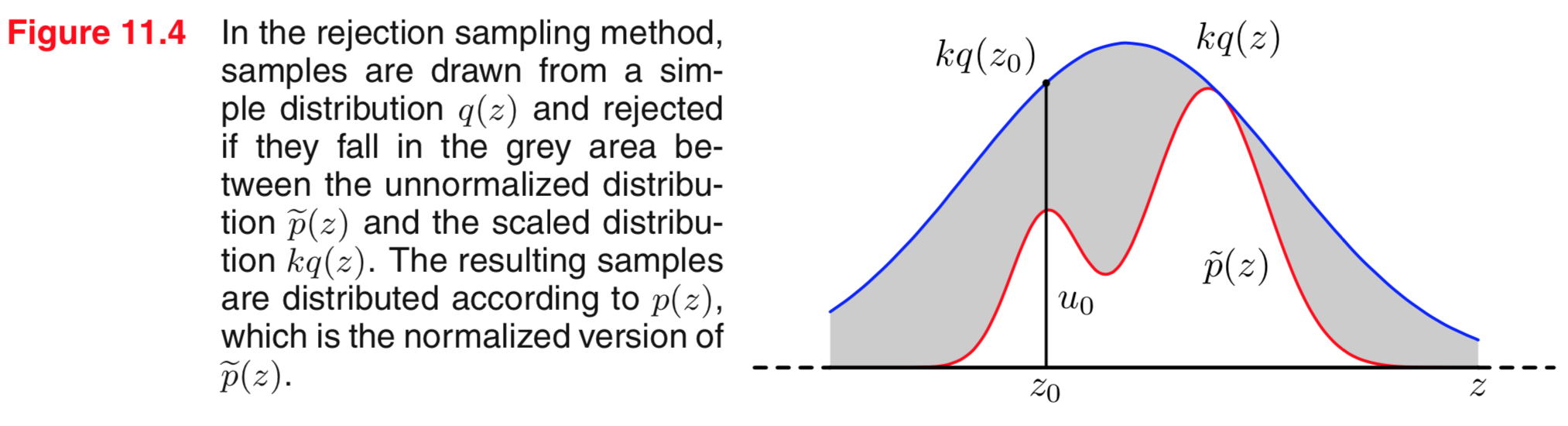
- kq尽可能和目标分布接近,否则采样效率很低,比如下述例子
## 利用拒绝采样a>1和b>1的beta分布随机变量 def reject_samping_beta(a, b): assert a>1 and b>1 reject = True z = 0 while reject: z = urnd() p = z**(a-1) * (1-z) ** (b-1) / beta(a, b) u = urnd() reject = u > p return z
- Gamma分布的例子
$$
Gam(z|a,b) = \frac{b^a z^{a-1} \exp(-b z)}{\Gamma(a)}, a>1
$$
选取$(c = a − 1, b^2 = 2a − 1)$,柯西分布 $(q(z) =\frac{k}{1 + (z − c)2/b^2})$ 选取足够小的k可以逼近gamma分布的包罗
重要性采样
- 不是生成目标分布的采样,而是直接近似在这个分布下的期望值。
- p(z) 容易计算,但是不容易生成该分布的采样,比如gamma分布
- 假设容易采样分布为q(z), 那么期望
$$
E_p[f] = \int f(z)p(z) dz = \int \frac{p(z)}{q(z)}f(z) q(z) dz \\
= E_q[\frac{p(z)}{q(z)}f(z)]
$$
其中$(\frac{p(z)}{q(z)})$为重要性权重 - 优点:所有的采样样本都保留了下来
- 缺点:跟拒绝采样一样,p和q分布要尽可能差异小,否则采样效率也比较低。比如总是采样到很小概率的区域
- sampling-importance-resampling SIR
- 先从分布q中采样L个样本$(z_1, ..., z_L)$
- 计算重要性权重(可以不用归一化概率) $(w_1,...,w_L)$
- 从L个样本中用重要性权重加权采样L个新样本$(z_1, ..., z_L)$
- 优点:所有样本都保留了下来, 能在一定程度上解决采样效率低的问题
- 缺点: L很小的时候存在的固有偏差较大。比如L=1的时候,会导致实际采样的分布等于q(z),只有到L趋近于无穷的时候,才没有偏差
采样与EM算法
- 蒙特卡洛EM算法,在求Q函数的时候,利用采样的方法来估计积分的值。
- 缺少一个例子来理解。。。。。。。。。。。
- IP算法P537页,以后再说
马尔科夫链蒙特卡洛MCMC
- 能够处理一大类分布的问题, 能够容易扩展到样本向量维度很高的问题
- 马尔科夫链平稳条件(充分条件) 意义是: 从z跳转到z'的联合概率,与从z'到z的联合概率相等
$$
p(z) T(z, z') = p(z') T(z', z)
$$ - 目标:构造一个马氏链, 稳态分布是目标分布p(z),就可以采样出无穷多的样本了
- 假设目标分布是p,用户构造出来的转移概率为q(z|z^{t}),利用拒绝采样的方法来配平上述平稳条件,假设接受概率为A(z|z^{t}),那么要求
$$
p(z^{t})q(z|z^{t})A(z|z^{t}) = p(z)q(z^{t}|z)A(z^{t}|z)
$$
为了使上式平衡,可以让接受率跟转移的联合概率成反比。选取$(A(z|z^{t}) = min(1, \frac{p(z)q(z^{t}|z)}{p(z^{t})q(z|z^{t})}))$
即,如果左边大于右边,那么右边以概率1接受,左边以小于1的概率接受。 - 一个变量,多个离散状态的情况模拟, 即让 i->j 的联合概率 等于 j->i 的联合概率
def rand_i(w): w = w/w.sum() j = 0 s = w[j] r = random.random() while s < r: j += 1 s += w[j] return j def MetropolisHastings(): p_target = [0.1, 0.2, 0.2, 0.5] q = np.ones((4,4)) * 0.25 x = np.random.randint(4) x0 = x rx = [] for i in range(100000): x = rand_i(q[x0]) aij = p_target[x] * q[x, x0] / (p_target[x0] * q[x0, x]) # 接受率 aij = min(1, aij) if urnd() > aij: continue if i> 10000: rx.append(x) x0 = x # update return rx
吉布斯采样
- 不用拒绝采样,直接通过巧妙地构造转移概率来实现等式配平。构造方法是:
- 以某个次序(具体的次序不重要,随机都行)选择z的某个维度z_i。
- 计算条件概率$(p(z_i|z_{i-}))$,$(z_{i-})$表示除了zi外的其他维度变量
- 用条件概率采样的zi代替当前的zi
- 这样一来,p(z)是联合分布的边际分布,q(z|z')是个路径相关的条件分布(参考下面说的2维的情况),所以等式左右两边都等于联合分布除以一个共同的常数,配平了!!
- 原因解释, 因为在每一步, 只变动一个维度,而且这个维度的采样概率只依赖于剩下的变量。因此容易验证
$$
A(z|z^{t}) = \frac{p(z)q(z^{t}|z)}{p(z^{t})q(z|z^{t})} = 1
$$ - 假设一维情况下, q(z|z') = p(z),所以等式两边都是 p(z)p(z')
- 假设2维情况
- 第一步 (x_1, y_1) -> (x_1, y_2); x_1不变,等式两边都是 p(x_1,y_1)p(x_1,y_2)/p(x_1) 是关于 y_1, y_2对称的
- 第二步 (x_1, y_2) -> (x_2, y_2); y_2不变,等式两边都是 p(x_1, y_2)p(x_2, y_2)/p(y_2) 是关于 x_1,x_2对称的
- 总的结果是等式左右两边都等于 p(x_1,y_1)p(x_1,y_2)p(x_2,y_2)/p(x_1)/p(y_2) 所以马氏链配平了
