投影算子
点到闭凸集合的投影
$$
prox_C(x) = \arg\min_y I_C(y) + \frac{1}{2}||x - y||^2
$$
其中$(I_C)$是集合C的示性函数
$$
I_C(x) = \begin{cases}
0, \quad x \in C \\
\infty, \quad x \not\in C
\end{cases}
$$
几何解释就是点x到集合C的投影就是C中到x最近的点!
把示性函数替换成一般的凸函数f,可以得到一般的投影算子
$$
prox_f(x) = \arg\min_y f(y) + \frac{1}{2}||x - y||^2
$$
不动点方程:如果一个点x*在f的投影下是他自己,那么根据上式,第二项为0,所以
$$
x^ * = prox_f(x^* ) = \arg\min_y f(x)
$$
几何解释就是在f的最小值等高面上的点的投影是它自己!
由于点x到投影点$(prox_f(x))$的方向向量$(x - prox_f(x))$与等高面垂直(投影的几何解释),因此,投影操作可以看做梯度下降的推广!
投影是往函数f的较小值等高面上进行投影!
令$(p = prox_{\lambda f}(x))$,
$$
p = \arg\min_y \frac{1}{2} ||y - x||^2 + \lambda f(y) \\
0 \in p-x + \lambda \partial f(p) \\
x \in (I + \lambda \partial f) (p) \\
p = (I + \lambda \partial f)^{-1} (x)
$$
注意,次梯度的逆有唯一的像!所以投影算子与次梯度关系为
$$
prox_{\lambda f} = (I + \lambda \partial f)^{-1}
$$
如果$(\lambda)$很小且f存在常规梯度,那么可以近似为
$$
prox_{\lambda f}(v) \approx v - \lambda \nabla f(v)
$$
也就是说 投影操作是梯度下降的一种推广!实际上,可以看做一种前向梯度下降,即下降的梯度不是在当前点v计算得到的,而是在下降的目标点p计算得到的!
如果投影操作计算方便(有简单的解析解),那么用投影操作做优化可以取代梯度下降,并且可以应用到梯度下降没法用的场景——梯度不存在的函数优化!
近似点算法:求函数f的最小值,利用投影算子是压缩算子,且投影算子的不动点是f的最小值点性质可得迭代近似点算法
$$
x_{n+1} = prox_{\lambda f}(x_n)
$$
前面说到投影算子就相当于梯度下降的推广,那么近似点算法可以看做梯度下降求最小值的推广!
Moreau 分解
点v可以分解为投影和共轭投影之和
$$
v = prox_f(v) + prox_{f^ * }(v) \\
f^ * (y) = \sup_x \left(y^T x - f(x)\right)
$$
这个分解可以看做几何中的正交分解!
近似梯度法
forward-backward splitting
如果目标函数存在不可微分部分,可以将目标函数分解为两部分,一部分可以微分,另一部分不可微分
$$
\min_x f(x) + g(x)
$$
假设f可微,g是不可微部分。若$(p)$是最优解,那么根据最优条件可知
$$
0 \in \lambda \nabla f(p ) + \lambda \partial g(p ) \\
0 \in \lambda \nabla f(p) - p + p+ \lambda \partial g(p ) \\
(I - \lambda \nabla f) (p) \in (I + \lambda \partial g) (p ) \\
p = (I + \lambda \partial g)^{-1} (I - \lambda \nabla f) (p) \\
p = prox_{\lambda g}\left( p - \lambda \nabla f(p) \right)
$$
上述不动点方程给出了优化迭代步骤,先按着可微函数梯度下降,然后对不可微函数做投影下降!
如果两步都采用投影来做
$$
p = prox_{ g}\left( prox_f (p) \right)
$$
就是 backward-backward splitting.
投影梯度算法
求解约束优化问题
$$
\min_{x \in C} f_2(x)
$$
迭代算法
$$
x_{k+1} = P_C\left(x_k - \gamma \nabla f_2(x_k)\right)
$$
$(P_C)$是到凸集的投影,该算法的集合意义是先沿着f2的梯度方向下降,让后将结果点投影到集合C中,以保证解不会离开约束区域!
交替投影算法
求解约束优化问题
$$
\min_{x\in C} \frac{1}{2} d_D^2(x)
$$
$(d_D(x))$是点x到凸集D的距离,采 backward-backward 分割,可得迭代算法
$$
x_{k+1} = P_C(P_D(x_k))
$$
该算法的几何图像是,交替像两个凸集C和D进行投影,直到收敛!
投影算子计算
常规的计算方法是直接根据定义,求解优化问题:
$$
\min_y f(y) + \frac{1}{2\lambda}||y - x||^2
$$
| $(dom f)$有限 | $(dom f = R^n)$ | |
|---|---|---|
| f光滑 | 投影梯度法、内点法 | 梯度下降 |
| f不光滑 | 投影次梯度法 | 次梯度法 |
二次函数
$(f(x) = 1/2x^T A x + b^T x +c )$,
$$
prox_{\lambda f} (v)= (I + \lambda A)^{-1}(y - \lambda b)
$$
如果 A = I, 且只有二次项,即$(f = || \cdot || _ 2^2)$,那么投影算子表现为shrinkage operator,直观来看就是把做了一个衰减!
$$
prox_{\lambda f}(v) = \frac{v}{1 + \lambda}
$$
标量函数
如果f是标量函数,自变量是单变量,那么很容易求得
$$
v \in \lambda \partial f(x) + x \\
x =prox_{\lambda f}(v) = (1 + \partial f)^{-1} v
$$
当$(f(x) = |x|)$时,有
$$
prox_{\lambda f}(v) = \max(|v| - \lambda , 0) sgn(v)
$$
即软阈值(soft thresholding)操作!
纺射集投影
集合$(C = \{x| Ax = b \})$,投影操作为
$$
\Pi_C(v) = v - A^\dagger(Ax - b)
$$
$(\dagger)$是伪逆。
当A是一个向量时,相当于投影到超平面,
$$
\Pi_C(v) = v - \frac{a^Tx-b}{||a||_ 2^2} a
$$
半空间
集合$(C = \{x| a^Tx \le b \})$,投影操作为
$$
\Pi_C(v) = v - \frac{(a^Tx-b) _ + }{||a|| _ 2^2} a
$$
即要减掉向量在另外一边的分量!
集合的支持函数
集合C的支持函数定义为
$$
S_c(x) = \sup_{y\in C}y^T x
$$
结合解释是,以x为外法向量的点就是支持点!支持函数与示性函数共轭$(S_C^ * = I_C )$。
根据Moreau分解,知
$$
prox_{\lambda S_c}(v) = v - \lambda \Pi_C(v/\lambda)
$$
注意最后一个式子的几何理解!
范数
如果函数$(f = || \cdot ||)$,那么对偶函数$(f^ * = I_B)$, B是对偶范数的单位球!
$$
prox_{\lambda f}(v) = v - \lambda \Pi_B(v/\lambda)
$$
L2范数
L2范数的对偶范数还是L2范数,L2单位球就是欧式空间的单位球!所以
$$
\Pi_B(v) = \begin{cases}
v/||v|| _ 2, \quad ||v|| _ 2 > 1, \\
v, \quad ||v|| _ 2 \le 1
\end{cases}
$$
所以L2范数的投影为
$$
prox_{\lambda f}(v) = \begin{cases}
(1 - \lambda/||v|| _ 2) v, \quad ||v|| _ 2 > \lambda, \\
0, \quad ||v|| _ 2 \le \lambda
\end{cases}
$$
也就是将原始向量v沿着v方向减少$(\lambda)$长度,除非减到0向量!也叫做 block soft thresholding操作!
L1范数
L1范数的对偶范数是$(L_{\infty})$,对应的单位球是单位立方体,投影为
$$
\Pi_B(v) = \begin{cases}
sgn(v_i), \quad |v _ i| > 1, \\
v_i, \quad |v_i| \le 1
\end{cases}
$$
所以
$$
v_{i+1} = \begin{cases}
v_i - \lambda, \quad v_i>\lambda \\
-v_i + \lambda, \quad v_i<-\lambda \\
0, \quad other
\end{cases}
$$
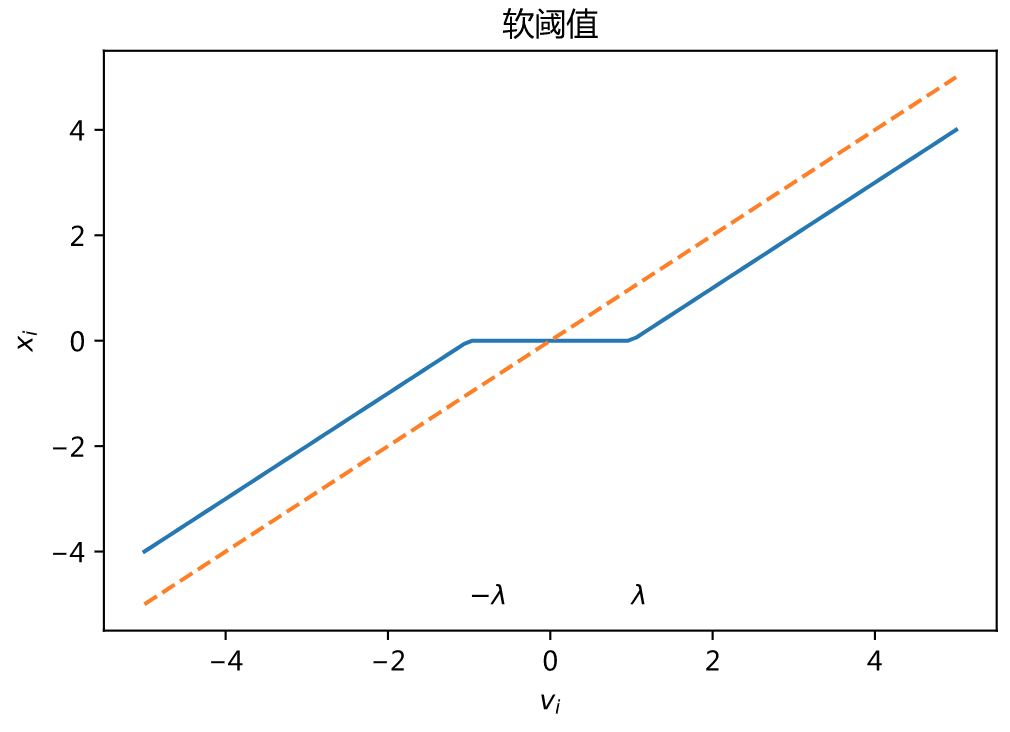
软阈值算法
L1范数正则
L1正则问题
$$
\min_x f(x) + \lambda |x|_ 1
$$
利用近似梯度法,令$(g=|\cdot| _ 1)$有迭代算法
$$
z_k = x_k - \eta \nabla f(x_k) \\
x_{k+1} = prox_{g} z_k
$$
最后一步是一个投影,根据定义
$$
prox_{\lambda g} (v) = \arg \min_x \lambda |x| _ 1 + \frac{1}{2}||x - v||^2
$$
对上式微分得
$$
v_i - x_i \in \lambda \partial |x_i|, i=1,...
$$
上式表明下降量不超过$(\lambda)$,如果$(v_i)$绝对值大于$(\lambda)$那么下降不会越过不可微分点,可以按照正常的梯度下降,
但是如果小于,那么只能下降到0,才能保证上式成立!
$$
x_i = \begin{cases}
v_i - \lambda, \quad v_i>\lambda \\
-v_i + \lambda, \quad v_i<-\lambda \\
0, \quad other
\end{cases}
$$
这表明,加了L1正则项,相当于将阈值为$(\lambda)$以内的分量都置0,以上的都减小$(\lambda)$。
L2范数
L21范数
软阈值算法实现
求解问题
$$
\min_x \frac{1}{2} ||Ax - b||^2 + \lambda_2 ||x|| _ 2^2 + \lambda_1 ||x|| _ 1
$$
可以看到,算法很快就收敛了,并且L1正则很容易得到稀疏解!
import numpy as np ## 问题100维 # n = 100 A = np.random.randn(n*10, n) # 超定方程 xx = np.random.randn(n) mask = np.random.rand(n)<0.8 xx = xx * mask print 'ground truth:', xx b = np.matmul(A, xx) + np.random.randn(n*10) * 0.1 # 加入一些噪声 >>> Output: ground truth: [ 0. 0.42171383 -0.94716965 0.54640995 0.67948742 0.88857648 0.14209921 -0.70685128 0.43310285 -1.2423563 0.27323468 -0.23007387 1.53049499 -0.03076339 -0. 0.53795911 1.1853585 0.66830622 0.0813316 -0.39508658 0.75451939 0.53967945 -0. -0.79440595 0.10416921 -0.76577241 2.21847433 -1.38163076 0.6089114 1.18767332 -1.28999937 0.65445551 -0.3248272 -0.88002173 -0.82729771 0.47309462 -0.8384278 -1.66928355 0.85613791 0.31921217 2.51727067 1.11885762 0.38646877 0.32068998 0. 1.02912399 -0.4607417 -0.84519518 -0. 0.34949314 0.56150765 0.08035849 1.812666 -1.23004836 1.65564242 0.23581581 -0.03529459 -0.33258733 -0.65909872 -1.1317373 -0.46223132 0.97113475 0. 0.17753836 -0. 0. 0.08929848 0.02685682 0. -0. 1.86521051 -1.02918525 1.39816556 -0.32507115 0.20111102 -0. -1.81123986 0.18043876 0. -0.84625861 0.8709556 0. 0.65961205 2.35225572 0. -0.04910171 -1.35667457 -1.45385942 0.15419398 1.1789595 0.7340732 -0. 0.85819805 0.57832173 0.49845621 0. -0.6047393 0.99361454 0.45679531 0.28392374] # 目标函数 def f(x, lab=1, lab2=0.01): return 0.5*np.sum((np.matmul(A, x) - b)**2 )+ lab * np.sum(np.abs(x)) + lab2*np.sum(x*x) # 除了L1正则项外的梯度 def grad(x, lab2=0.01): return np.matmul(A.T, np.matmul(A, x) - b) + lab2*x # 软阈值迭代算法 x = np.random.randn(n) mu = 0.001 lamb = 0.01 lab2 = 0.01 for i in range(100): # STEP1:梯度下降 x -= grad(x, lab2) * mu # STEP2:投影操作,也就是软阈值操作 for j in range(len(x)): if x[j] > lamb: x[j] -= lamb elif x[j] < - lamb: x[j] += lamb else: x[j] = 0.0 # 打印中间迭代结果 if i % 10 == 0: print i, 'loss=', f(x, lamb, lab2) print x >>> Output: 0 loss= 7532.16879981 10 loss= 11.0285759018 20 loss= 10.9840030328 30 loss= 10.9842744582 40 loss= 10.9842770859 50 loss= 10.9842771092 60 loss= 10.9842771094 70 loss= 10.9842771094 80 loss= 10.9842771094 90 loss= 10.9842771094 [ 0. 0.41005474 -0.93416517 0.52872225 0.66901803 0.87710187 0.1254697 -0.69410934 0.42094427 -1.23128115 0.25644887 -0.22262353 1.51692245 -0.02018758 0. 0.53116499 1.17967392 0.64459272 0.06787308 -0.38043066 0.74631218 0.52152388 0. -0.79768153 0.09135038 -0.75555311 2.20245087 -1.36570672 0.59778203 1.17212485 -1.27509079 0.63889237 -0.31797818 -0.87161519 -0.81344888 0.464237 -0.82969714 -1.66337076 0.83671452 0.30766759 2.50494207 1.1034511 0.38148637 0.31093457 0. 1.02118932 -0.45228788 -0.8302418 0. 0.32929066 0.54006833 0.06742762 1.80640673 -1.2229943 1.64774712 0.21735476 -0.02296309 -0.3222897 -0.65161403 -1.10748401 -0.44978335 0.95982422 0. 0.16099326 -0.00337374 0. 0.0845288 0.01798603 0. 0. 1.84882179 -1.01734222 1.39139325 -0.31544124 0.18957113 0. -1.80153297 0.17600738 0. -0.83960423 0.86347204 0. 0.64546066 2.35318802 0. -0.03208243 -1.34212428 -1.44773413 0.14815159 1.17458127 0.72367534 0. 0.84649559 0.56543654 0.47495661 0. -0.59702874 0.98713984 0.4507846 0.27214572]
交替方向乘子ADMM
求目标可分解优化问题
$$
\min_{x,z} f(x) + g(z) \\
s.t. \quad Ax + Bz = c
$$
利用增广拉格朗日乘子
$$
L_{\rho}(x, z, y) = f(x) + g(z) + y^T(Ax + Bz - c) + \rho/2 ||Ax+Bz-c||^2
$$
利用拉格朗日对偶问题的性质可知,在强对偶条件下,最优解为
$$
x * , y * , z * = \arg\max_y (\arg\min_{x,z} L(x,z, y) )
$$
于是有交替迭代算法(ADMM):
$$
x_{k+1} = \arg\min_x L_{\rho}(x, z_k, y_k) \\
z_{k+1} = \arg\min_z L_{\rho}(x_{k+1}, z, y_k) \\
y_{k+1} = y_k + \rho (Ax_{k+1} +Bz_{k+1} - c)
$$
其中前两个式子实际上是两个投影算子,最后一个式子是用梯度上升求对偶函数的最大值!
当A=-B=I时,可得到无约束最优化问题$(\min_x f(x) + g(x))$的求解算法
$$
x_{k+1} = prox_{\lambda_k f}(z_k - u_k) \\
z_{k+1} = prox_{\lambda_k f}(x_{k+1} + u_k) \\
u_{k+1} = u_k + x_{k+1} - z_{k+1}
$$
多个函数
优化如下问题,其中这些函数都有可能是不光滑的
$$
\min f_1(x) + ... + f_m(x)
$$
将问题转化为约束优化问题
$$
\min_{x \in D} f(x) \\
f(x) = f_1(x_1) + ... + f_m(x_m) \\
x = (x_1, ..., x_m), D= {(x_1,...,x_m) | x_1=...=x_m}
$$
相关资料
- 比较全面介绍近似算法的书;Parikh N, Boyd S. Proximal algorithms[J]. Foundations and Trends® in Optimization, 2014, 1(3): 127-239.
- 近似算法综述论文:Combettes P L, Pesquet J C. Proximal splitting methods in signal processing[M]//Fixed-point algorithms for inverse problems in science and engineering. Springer, New York, NY, 2011: 185-212.
- 分布式ADMM经典论文:Boyd S, Parikh N, Chu E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends® in Machine Learning, 2011, 3(1): 1-122.
- 压缩感知书籍:Foucart S, Rauhut H. A mathematical introduction to compressive sensing[M]. Basel: Birkhäuser, 2013.