等式约束问题

对于线性方程等式约束问题

$$
\begin{align}
\min \quad & f(x) \\
s.t. \quad & A x =b
\end{align}
$$

根据KKT最优条件可知最优解满足方程

$$
Ax^ * = b, \nabla f(x^ * ) + A v^ * = 0
$$

后一个式子实际上是说，在最优解处，f的梯度在A列向量的子空间中！A是向量的时候，有个直观的几何解释！即f的等高面与超平面相切！

等式约束二次规划 有闭式解，上述条件变成了一个线性方程问题！设$(f(x) = 1/2 x^T P x + q^T + r)$，那么KKT条件变为

$$
Ax^ * = b, P x^ * + A v^ * + q = 0
$$

这是一个线性方程，可以利用线性方程求解方法如高斯消元法、迭代算法等求解。
如果方程有解，那么所有的解都是可行解！如果方程无解，那么表示原问题没有最小值！

消除等式约束 方法：先求解线性方程得到通解 $(\{Fz + \hat{x}| z \in R^{n-p}\})$，然后代入目标函数，消除等式约束！

求解对偶问题 : 对偶问题是无约束优化问题。

$$
\min_v b^T v + f^ * (-A^T v)
$$

牛顿方法 即在迭代点附近用一个二次函数近似f(x)，这样一来，在每次迭代的时候，就是在求解等式约束二次规划，有闭式解！从而可以很方便求出下降步长！

内点法

凸优化问题

$$
\begin{align}
\min \quad & f(x) \\
s.t. \quad & f_i(x) \le 0 \\
& Ax=b
\end{align}
$$

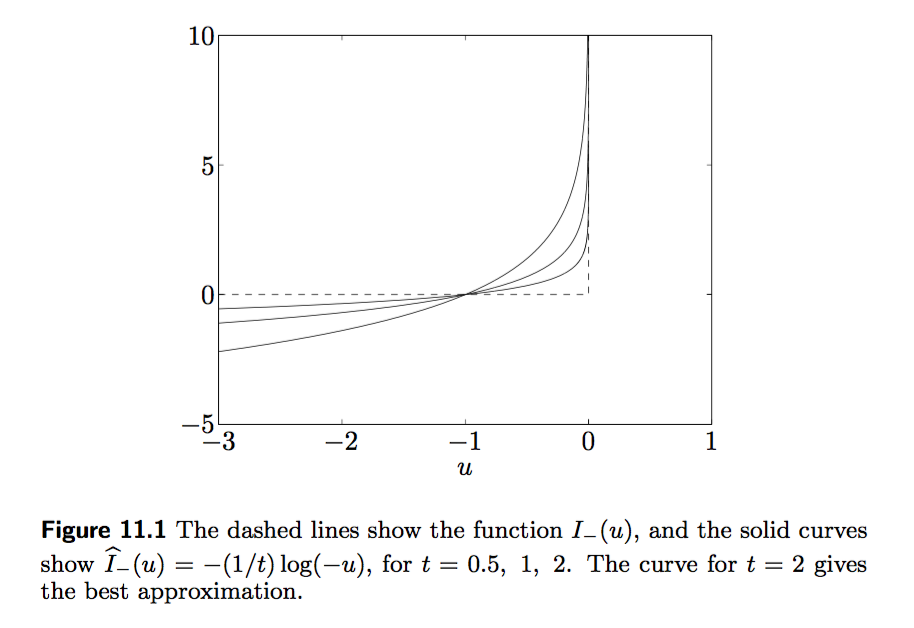
定义示性函数

$$
I_-(x) = \begin{cases}
0 \quad x \le 0 \\
\infty \quad x > 0
\end{cases}
$$

通过这个示性函数，可以将不等式约束去

$$
\begin{align}
\min \quad & f(x) + \sum_i I_-(f_i(x))\\
s.t. \quad & Ax=b
\end{align}
$$

对数壁垒函数：由于示性函数不可微，可以用可微函数近似，一种选择是采用如下对数函数

$$
\hat{I_-}(x) = - \frac{1}{t} \log(-x)
$$

随着参数t趋近于无穷大，对示性函数的近似度越来越好！在这种壁垒函数选取下，最优解可以通过牛顿法求解，最优解跟t有关，$(x(t))$随t变动而形成的轨迹叫做 中心路径。并且有

$$
f(x^ * (t) ) - p ^ * < m/t
$$

m是不等式约束的个数。p是最优f值，$(x^ * (t) )$是壁垒函数近似的最优解！因此，随着t增大，可以控制误差在指定的范围内！