参考

• 论文: Ricky T. Q. Chen, Yulia Rubanova, Jesse Bettencourt, David Duvenaud. "Neural Ordinary Differential Equations." Advances in Neural Processing Information Systems. 2018. arxiv
• 代码: https://github.com/rtqichen/torchdiffeq

摘要

• 用神经网络拟合隐态的梯度, 通过ODE Solver 求解输出

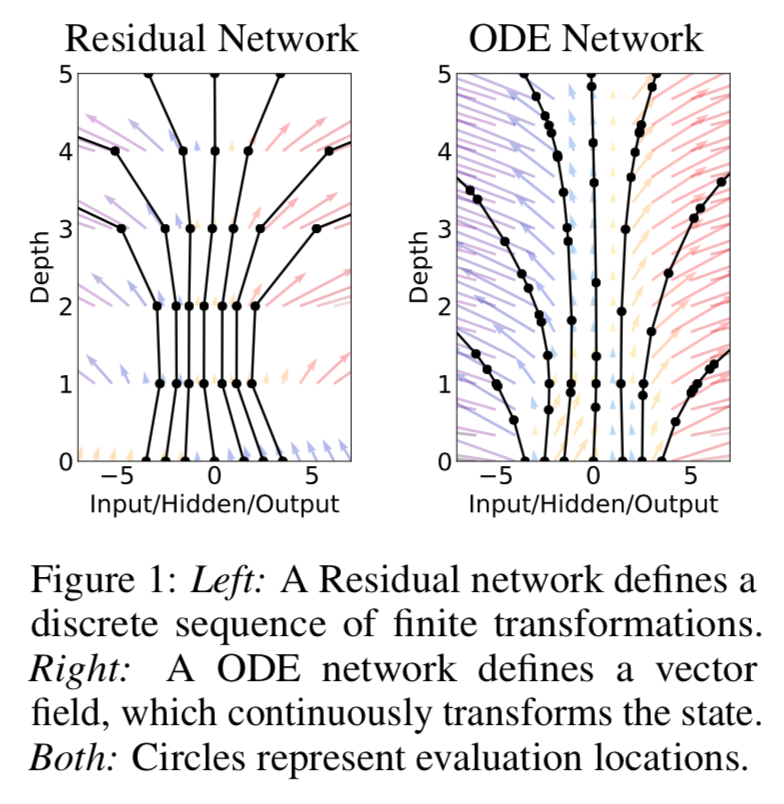
残差网络可以看做一个常微分方程初值问题的差分形式

resnet

$$
h_{t+1} = h_{t} + f(h_t, \theta_t), t=0, 1,2,... \\
h_0 = input
$$

ode

$$
\frac{d h(t)}{d t} = f(h(t), \theta, t) \\
h_0 = input
$$

相当于在不同的时间上,参数共享! 所以 参数/内存复杂度跟步长/层数无关!

另外,由于现代的 ODE solver 可以自适应调整以达到给定的精度。

此外, 可以应用到连续时间动态系统的优化中!

反模式的自动微分

假设标量损失函数$( L() )$的输入是 ODE solver 的输出, 也就是把 z(t) (你可以理解为神经网络最后一层隐向量)输入到损失函数中(例如logloss,rankloss等)
$$
L(z(t_1)) = L \left( \int_{t_0}^{t_1} f(z(t)), t, \theta dt \right) = L(ODESolver(z(t_0), f, t_0, t_1, \theta))\\
\frac{d z(t)}{d t} = f(z(t), \theta, t)
$$

为了优化L,需要计算L对参数的梯度。

adjoin $( a(t) = \partial{L} / \partial{z(t)} )$ 满足如下ODE(两边对t求导), 注意标量场L的散度等于0
$$
\frac{d a(t)} {d t} = - a(t)^T \frac{\partial f(z(t), t, \theta)}{\partial z}
$$

这表明,我们可以从a(t1)反向计算积分得到a(t0)
$$
a(t_0) = \int_{t_1}^{t_0} - a(t)^T \frac{\partial f(z(t), t, \theta)}{\partial z} dt
$$
这个类似于多层神经网络的BP过程。

L对参数$(\theta)$的梯度
$$
- \frac{d L} {d \theta} = \int_{t_0}^{t_1} a(t)^T \frac{\partial f(z(t), t, \theta )}{\partial \theta} dt
$$

算法参考文献: Optimization and uncertainty analysis of ODE models using second order adjoint sensitivity analysis