关于

论文：node2vec: Scalable Feature Learning for Networks

摘要

• 将一个网络中的节点变成一个低维的连续向量，作为其他模型的输入特征。
• 通过最大化网络邻居的似然函数。
• 基于特征值分解的线性或非线性降维方法在实际的大规模数据应用中，计算太慢？并且性能还不好！
• 目标函数，保证邻居节点依然相近；保证具有相似结构的节点的嵌入向量也相近！

• 目标函数：maximize the likelihood of pre- serving network neighborhoods of nodes in a d-dimensional feature space。
• 2阶 random walk 方法产生节点的网络上的邻居样本。
• node2vec可扩展到边
• 用学到的向量去做分类任务的特征，结果比其他方法好很多，并且这种方法很鲁棒！即使缺少边也没问题。
• 可扩展到大规模 node！
• 基于特征值分解的方法难以扩展到大规模？suffer from both computational and statistical performance drawbacks；不够鲁邦！不能

特征学习框架

• 网络：$(G = (V, E))$
• 学习目标：$(f : V \rightarrow R^d)$，实际上是一个$(|V| \times d)$参数
• 采样策略$(S)$生成的节点$(u)$的网络邻居 $(N_S(u) \in V)$
• 极大似然估计：

$$
\max_f \sum_{u \in V} \log Pr(N_S(u)| f(u) )
$$

• 几个假设：
  • 条件独立：$( Pr(N_S(u)| u ) = \Pi_{n_i \in N_S(u)} Pr(n_i|f(u)) )$
  • 对称性：特征空间中，两个互为邻居的边有对称效应：

$$
Pr(n_i|f(u)) = \frac{\exp(f(n_i) \dot f(u))}{\sum_{v\in V} f(v) \dot f(u)}
$$

和 word2vec 一样，可以通过负采样来优化分母的计算量！

• 最大的问题是对领居节点的采样，skip-gram是通过一个固定宽度的滑动窗，网络由于不是线性的，比较麻烦。不一定是直接邻居可以当邻居，这取决于采样策略 $(S)$

邻居节点的搜索策略

• 经典的搜索策略：
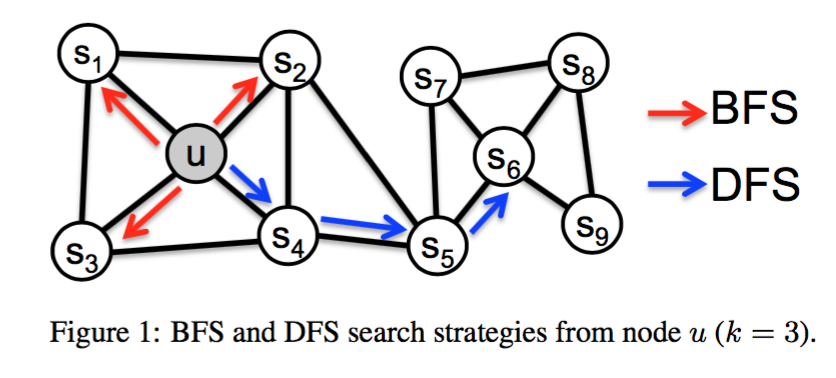
  • BFS：宽度优先搜索，找直接相连的节点
  • DFS：深度优先搜索
• node2vec 的搜索策略综合了这两种策略

• 对于源节点$(u)$，通过 random walk (马尔科夫链) 采样 l 长度的邻居节点 $(c_i, c_0=u)$
• 条件概率为：

$$
P(c_i=x|c_{i-1}=v) = \begin{cases}
\frac{\pi_{vx}}{Z}, if (v,x) \in E. \\
0, otherwise
\end{cases}
$$

其中$(\pi_{vx})$是未归一化的概率，Z是归一化常数。对于最简单的情况，可以用边的权重作为未归一化概率
$(\pi_{vx} = w_{vx})$。

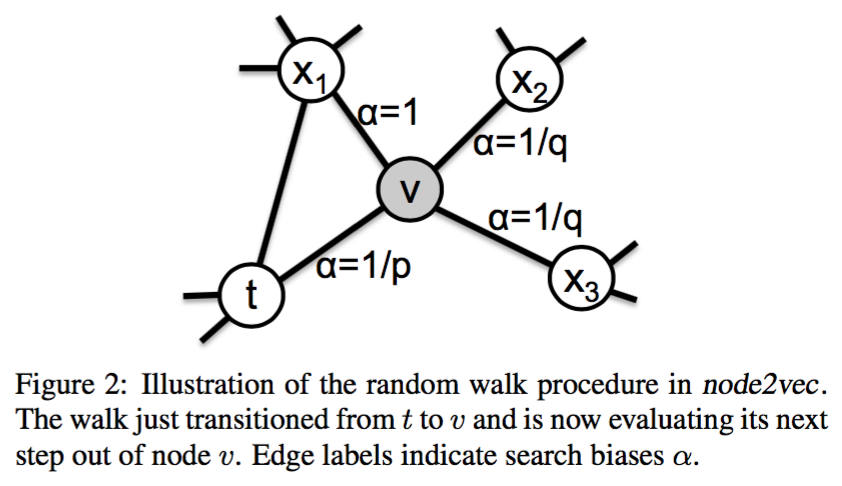
对于2阶 random walk，未归一化概率和权重之间的关系为：$(\pi_{vx} = \alpha_{pq}(t,x)w_{vx})$
t是上一个节点，v是当前节点，x是下一个可能的节点，系数

$$
\alpha_{pq}(t, x) = \begin{cases}
\frac{1}{p}, d_{tx} = 0, \\
1, d_{tx}=1,\\
\frac{1}{q}, d_{tx}=2.
\end{cases}
$$

$(d_{tx})$是两个节点的距离，p是return参数，q是in-out参数。

• random walk 的好处：
  1. 可以减少邻居的存储空间到$(O(a^2|V|))$.本来是$(O(E))$。
  2. 每一次产生的链可以复用，因为马尔科夫性。