关于
RNN相当于给神经网络加了记忆单元,做个类比,普通的前馈神经网络(DNN,CNN)就好像是组合逻辑电路;
而增加了记忆单元的 RNN (LSTM etc)就好像是时序逻辑电路。有了记忆单元的神经网络就能够像图灵机
一样记忆、推断等高级能力,而不仅仅是像组合逻辑那样只能学一个数学函数!
Memory Network
- [1] Memory Network, Jason Weston, Sumit Chopra & Antoine Bordes, Facebook AI Research 2015.
- [2] End-To-End Memory Networks, Sainbayar Sukhbaatar, Arthur Szlam, Jason Weston, Rob Fergus 2015.
RNN 的缺点在于记忆单元太小,所以记忆能力很弱,比如最简单的问题:输入一串单词,输出刚看到的单词,RNN都难以实现(Zaremba & Sutskever, 2014)
结构:一个记忆单元集合 $( m = (m_1,m_2, ...) )$,4个模块:
- I : input feature map, 将输入转换为中间特征表达。
- G : generalization, 根据新的输入更新存储单元的内容。
- O : output feature map, 根据当前的输入和存储单元内容,生成输出结果的特征空间表达。
- R : response, 将输出的特征空间表达转换为目标形式,例如一个文本,或者一个动作。
给定一个输入 x,例如一个句子,一个视频,
- 首先将输入转换为中间表达 $( I(x) )$
- 对新的输入x,更新内存 $(m_i = G(m_i, I(x), m), \forall i)$
- 对新的输入x 和内存m,计算输出向量 $( o = O(I(x), m) )$
- 最后解码输出序列 r = R(o)
A MemoryNN Implement for Text
如果上述四个组件是用神经网络来实现,就称作 Memory NN,这些组件可以用任何机器学习的方法!
基本模型
输入是一个句子(I),文本被存在下一个空的记忆单元,不做任何处理(G),O 模块根据输入 x 找到k个有关的记忆单元,
$$
o_j = O_j(x, m) = \arg\max_{i=1,...,N} s_O([x, m_{o_1}...,m_{o_{i-1}}], m_i)
$$
最终输出给 R 的是 $( [x, m_{o_1},..,m_{o_k}] )$,在这个例子中,R根据这些记忆单元和输入,
输出一个最匹配的单词
$$
r = \arg\max_{w \in W} s_R([x, m_{o_1},..,m_{o_k}], w)
$$
这个任务可以用来实现单个单词的问答问题。
两个匹配函数$(s_O, s_R)$都可以用下列方式建模
$$
s(x, y) = \phi_x(x)^T U^T U \phi_y(y)
$$
U 是要学习的参数,$(\phi)$是对输入的 embedding 函数。
训练
学习最优的参数 $(U_O, U_R)$ 最小化损失函数,损失函数包含2部分(k=2),
- 选择最匹配的记忆单元带来的风险
- 选择最佳response带来的风险,如果用RNN就直接用RNN的损失函数就行
上述风险都用大间隔损失函数来刻画!
词序列作为输入
没有区分 statements 和 questions,因此需要学习一个分割函数,将词序列分割为两部分。
$$
seg(c) = W_{swg}^T U_S \Phi_{seg}(c)
$$
上述三个参数分别是:分割模型的线性权重参数,将特征空间映射到embedding空间的线性变换矩阵(即查找表),输入词的特征向量(高维稀疏),c是词袋词典。
EFFICIENT MEMORY VIA HASHING
利用 hash trick 加速内存查找:将输入 I(x) hash到一个或多个桶,只将输入和同一个桶内的 memory 进行打分计算。
两种 hash 策略:
- 直接 hash 词,因此对于一个句子,只需比较至少共享一个词的 memory
- 对词向量做 k-means 聚类,对一个句子,比较的是和至少一个词在同一个类别的memory,这种方法考虑了词的语义。
MODELING WRITE TIME
将 memory 写的时间也记录下来。 对内存 $(m_j)$ 将索引 j (假定没有内存更新,索引和时间一一对应)也编码进 $(\Phi_x, \Phi_y)$。具体做法,将 $(\Phi)$ 扩充三维,都设置为0,对输入 x ,当前两个内存 y, y', 计算分数
$$
s(x, y) = \phi_x(x)^T U_{O_t}^T U_{O_t} (\phi_y(y) - \phi_y(y') + \phi_t(x, y, y') )
$$
其中$(\phi_t(x, y, y'))$只有扩充的三维不为0,其他都为0,扩充的三维分别用于指示
- whether x older than y,
- whether x older than y',
- whether y older than y',
实际上将原来的 poinwise 变为 pairwise了,并加入了时间先后关系信息。选出比较完胜的y作为输出。
对于unseen词的处理
利用语言模型,用周围的词预测这个词可能是什么词,那么这个unseen的词就和这个预测的结果的词相似。
将词特征表达从 3|W| 增加到 5|W|,增加的两个部分分别表达这个词的左上下文和后上下文。
精确匹配
embedding 因为将词降维到低维连续向量,所以无法做精确匹配。
解决的办法是为 score 增加一项精确匹配score。
$$
s(x, y) = \phi_x(x)^T U^T U \phi_y(y) + \lambda \phi_x(x)^T \phi_y(y)
$$
结果
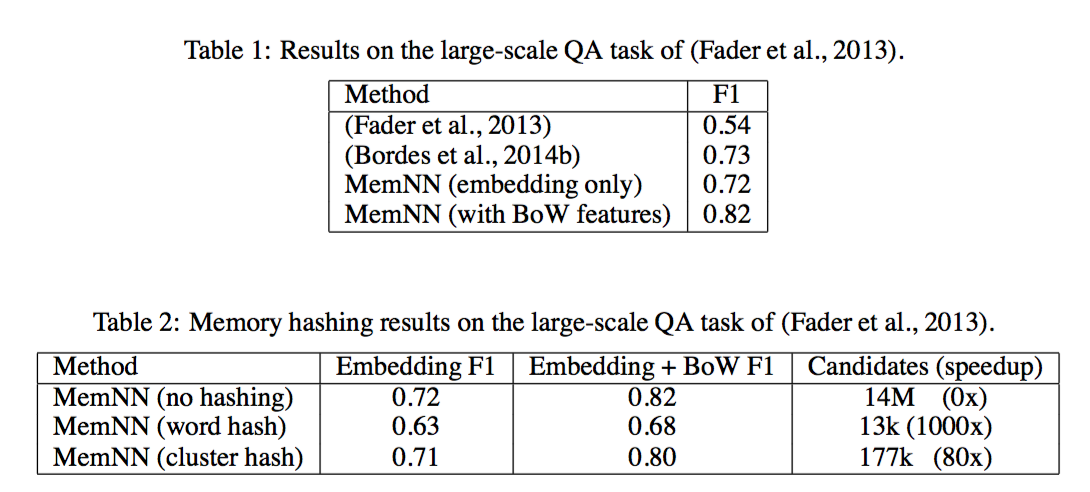
- 可以看出 只用 embedding 特征和之前最好结果差不多,稍低,但是加上 BOW 特征,效果马上就提升了9个点。
- 不同hash策略的影响,word hash 实现了1000倍的加速但是精度减少很明显,cluster hash 在精度只减少1个点的情况下,实现了80倍的加速。
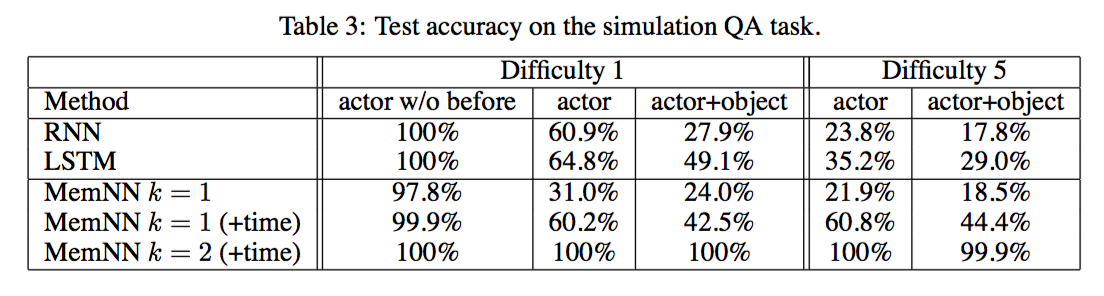
- 可以看到时间特征对提升非常显著
- 输出选取的内存个数k对效果提升也非常显著
- MemNN 完胜 RNN,LSTM
End-To-End Memory Networks
Neural Turing Machine
图灵机三个基本机制:元素操作(算数计算),逻辑流控制(分支),外部存储。
现代机器学习模型侧重建模复杂数据,缺乏流控制和存储。
RNN 是图灵完备的,即可以实现图灵机的所有操作,即可用图灵机完成的事情,RNN有这种潜能可以解决!
NTM之于RNN,就如图灵机之于有限状态机!最大的区别在于前者有接近无限的存储空间!
NTM 通过 attention 机制实现内存的读取和写入操作。
基础研究
这一部分主要是从心理学、神经科学、语言学等角度阐述 working memory 和 NTM 的相关原理和解释!
总之一句话:memory是非常重要的。
working memory 在心理学中用于解释短期信息处理能力
- Baddeley, A., Eysenck, M., and Anderson, M. (2009). Memory. Psychology Press.
- Miller, G. A. (1956). The magical number seven, plus or minus two: some limits on our capacity for processing information. Psychological review, 63(2):81.
Recurrent Neural Networks
与隐马尔科夫模型比较,前者只有有限个离散的状态,而 RNN 的状态是 distributed,具有无限个状态,具有更大的计算能力!
- state:隐马尔科夫模型具有有限个离散状态;RNN具有无限个分布式状态
- 状态转移概率:隐马尔科夫模型通过转移概率矩阵建模,依赖于当前状态和当前的输入;RNN通过隐层建模,可以是简单的RNN隐层单元,LSTM单元,GRU,甚至更复杂的多层结构,依赖于当前状态和当前的输入。
- 输出:只依赖于当前的状态,通常用生成模型建模这个条件概率;RNN则用(单层或多层)神经网络建模这个条件概率。
- 模型训练:隐马尔科夫模型根据输出的结果,用维特比算法解码出状态,转移概率和条件概率通过EM算法优化得到(参考语音识别);RNN则是端到端用梯度下降联合优化所有参数得到。
-
LSTM 解决RNN梯度消失和爆炸的问题是通过嵌入一个理想积分器?
-
RNN 的一些应用场景:
- 语音识别
- Graves, A., Mohamed, A., and Hinton, G. (2013). Speech recognition with deep recurrent neural networks. In Acoustics, Speech and Signal Processing (ICASSP), 2013 IEEE International Conference on, pages 6645–6649. IEEE.
- Graves, A. and Jaitly, N. (2014). Towards end-to-end speech recognition with recurrent neural networks. In Proceedings of the 31st International Conference on Machine Learn- ing (ICML-14), pages 1764–1772.
- 语音识别
神经图灵机结构
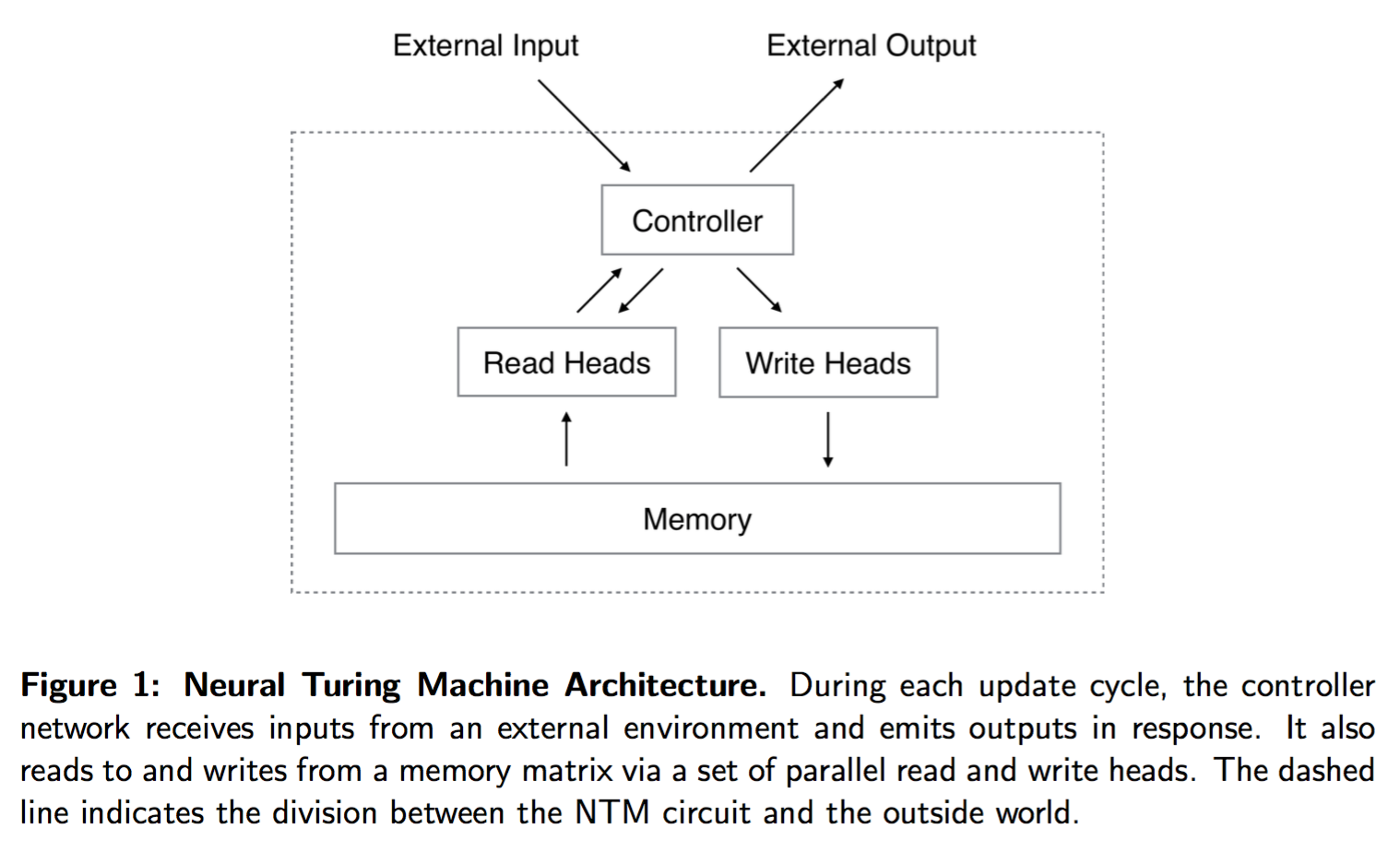
神经图灵机包括两个基础结构:神经网络控制器 controller,memory bank.
控制器通过输入向量和输出向量和外界交互,和一般的神经网络不同的是,他还会选择性地和内存交互。
和内存交互的部件成为 head,读写头。读写头通过 attention 机制,对不同的内存读取的值赋予不同的权重!
读写头要读所有的内存岂不是很慢,如何实现稀疏的读和写?
几个参数:
- $( \mathbf{M}_t )$ $(N \times M)$ 尺寸的内存矩阵,M是每个内存向量的尺寸,N是内存向量的个数
- $( \mathbf{w}_t )$ 是读头给出的每个内存的权重向量,他应该满足概率约束条件,非负,和为1.
- 读头读内存后返回的结果为
$$
\mathbf{r}_t = \sum_i w_t(i) \mathbf{M}_t(i)
$$
$( \mathbf{M}_t(i) )$ 是行向量,也就是一个内存单元。
写入过程:借鉴了 LSTM 的设计,写过程包括两个部分,forget 和 add.
- 擦除向量 $(\mathbf{e}_t)$ M 个元素全为0-1之间,设写入权重为$(w_t(i))$内存更新方程为
$$
\tilde{\mathbf{M}}_t(i) = \mathbf{M}_{t-1}(i)[\mathbf{1} - w_t(i)\mathbf{e}_t]
$$
- add 向量 $(\mathbf{a}_t)$,用add 向量更新擦出后的内存
$$
\mathbf{M}_t(i) = \tilde{\mathbf{M}}_t(i) + w_t(i) \mathbf{a}_t
$$
- 擦除向量和add向量每一维都是独立的。
寻址机制
即确定读写权重$(w_t)$
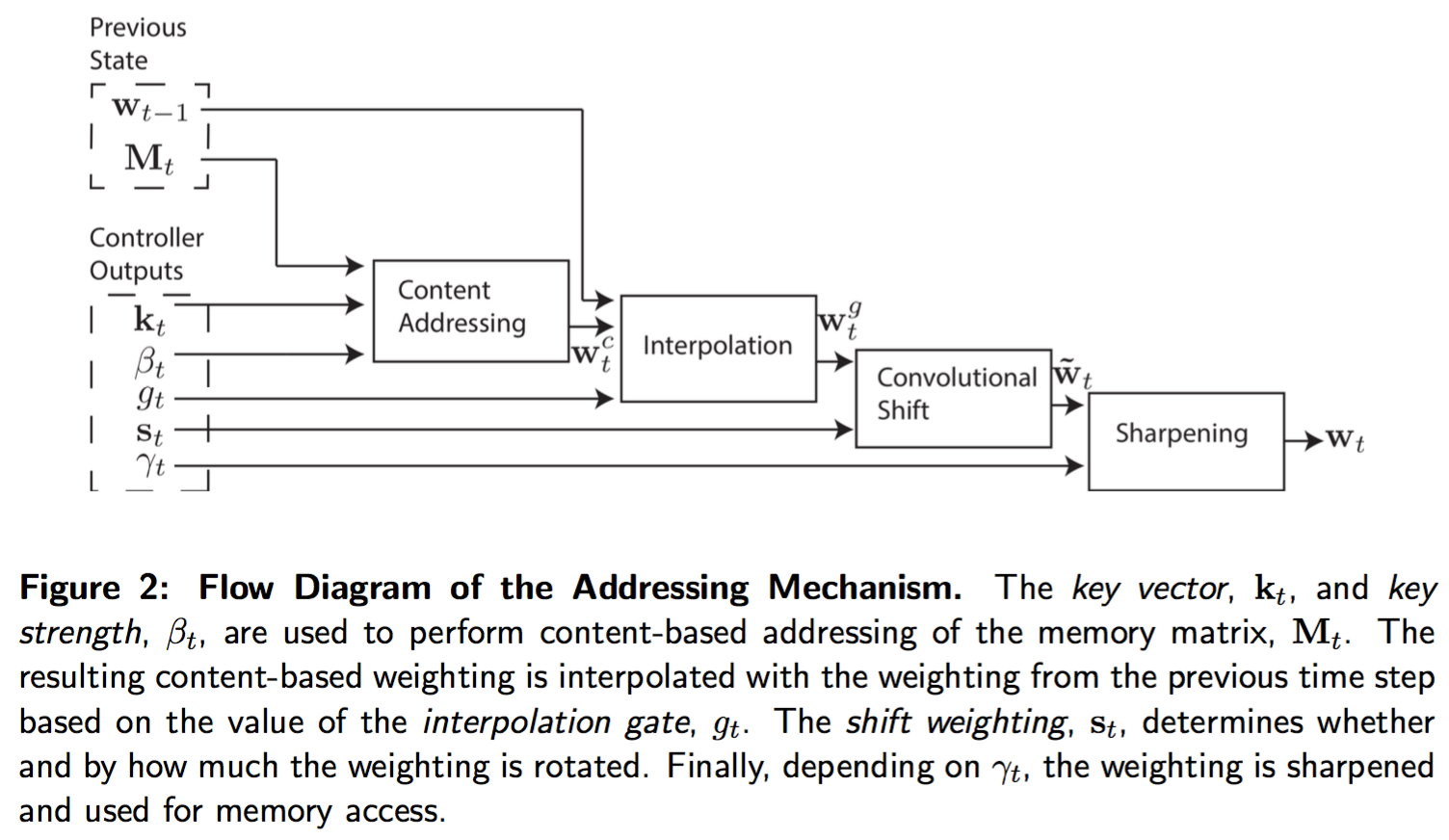
-
两种基本机制:
- 基于内容的寻址:找和控制器发出的值最相似的位置,Hopfield networks 1982:简单、可以获取内存的精确值;不适合算术问题,例如计算 $(x+y)$,寻址跟内容无关
- 基于位置的寻址,可以看做基于内容的寻址的特例,因为位置也可以看做内容的一部分
-
基于内容的寻址原理:每一个 head(读或者写)先生成一个长度为 $(M)$ 的 key vector $(\mathbf{k}_t)$,通过这个向量和内存中的所有向量进行比较,计算相似度 $(K[·, ·])$,相似度在所有的内存上归一化,$(\beta_t)$ 是缩放因子。论文中相似度度量采用向量的余弦相似度
$$
w_t^c(i) = \frac{\exp\left(\beta_t K[\mathbf{k}_t, \mathbf{M}_t(i)]\right)}{\sum_j \exp\left(\beta_t K[\mathbf{k}_t, \mathbf{M}_t(j)]\right)}
$$
- 基于位置的寻址:每一个 head 生成一个标量 interpolation gate $(g_t \in (0, 1) )$,利用这个门去控制当前权重向量$(\mathbf{w}t^c)$ 和历史权重$(\mathbf{w})$混合生成门限权重
$$
\mathbf{w}_{t}^g = g_t \mathbf{w}_t^c + (1 - g_t) \mathbf{w}_{t-1}
$$
经过插值后,head生成一个shift weighting $(\mathbf{s}_t)$,它是一个向量,刻画了移动的所有可能的整数上的一个分布。这个权重可以通过一个 softmax 层近似,也可以输出单个标量,例如6.7代表$(s_t(6) = 0.3, s_t(7) = 0.7)$,其他都为0. 利用这个向量对插值后的向量加权,可以表达为一个循环卷积
$$
\tilde{w}_t(i) = \sum_{j=0}^{N-1} w_t^g(j) s(i - j)
$$
为了让寻址更加sharp,head 还生成一个变量 $(\gamma_t \ge 1)$,对卷积后的权重做变换得到最终的权重
$$
w_t(i) = \frac{\tilde{w}_t(i)^{\gamma_t}}{\sum_j \tilde{w}_t(j)^{\gamma_t}}
$$
实验结果
未解决的问题
- 擦除向量$(e_t)$和add向量$(a_t)$怎么确定?
- 输入数据如何影响读写头的权重?输入数据和 key vector $(k_t)$ 有什么关系?