关于
这本书从概率的角度阐述机器学习相关理论,角度比较有意思!贝叶斯学派?!
Logistic Regression
- 生成模型,建模$(p(x, y))$,然后利用贝叶斯公式得到后验概率$(p(y|x))$.
- 判别模型,直接建模$(p(y|x))$.
逻辑回归模型:$( p(y|x, w) = Bernoulli(y| sigm(w^T x) )$
模型拟合
极大似然MLE:
负对数似然函数(也叫交叉熵)
$$
NLL(w) = - \sum_{i=1}^N \left[ y_i \log \mu_i (1-y_i) \log (1-\mu_i) \right]
$$
另外一种写法:$(y \in \{-1, +1\})$,那么$(p(y) = \frac{1}{1+\exp(y w^T x)})$。
所以
$$
NLL(w) = - \sum_{i=1}^N \log(1+\exp(y_i w^T x))
$$
closed form: 由常数,变量,通过四则运算,n次方,指数,对数,三角函数,反三角函数,经过有限次运算和符合得到的表达式(通常没有极限运算)
一个问题被称为可解的(P问题),表示可以用闭形式解决!?
很多累积分布没有闭形式,但是可以通过误差函数、gamma函数表达!
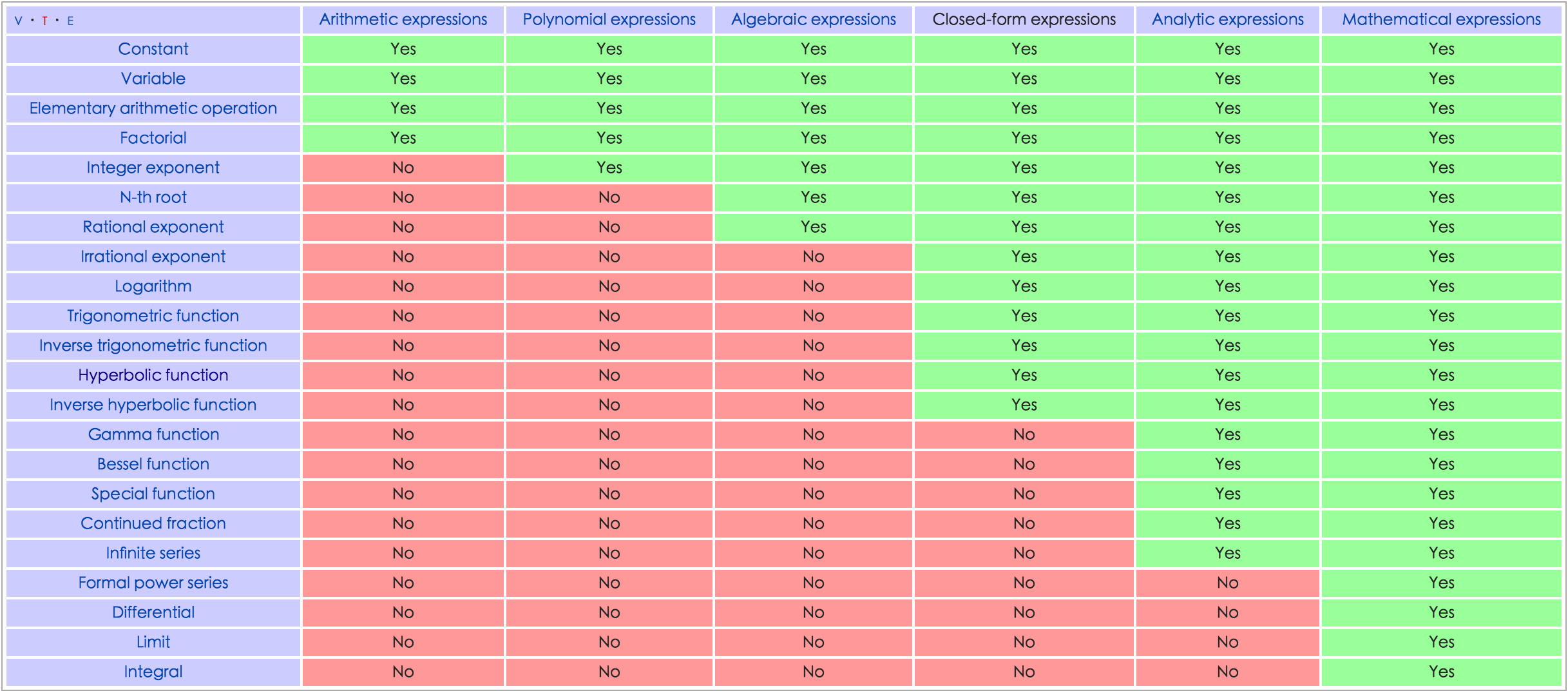
NLL 无法表达为闭形式?所以,采用数值优化,需要计算梯度和海森矩阵!
$$
g = X^T (\mu - y) \\
H = \sum_i \mu_i (1-\mu_i) x_i x_i^T = X S X^T
$$
H 是正定的,所以NLL是强凸函数,且存在唯一解。
最速下降,学习率通过线性搜索寻找。精确线性搜索的问题:zig-zag,当初始梯度和末端梯度正交,现象明显。
$(\eta_k = \arg \min_{\eta>0} f(\theta + \eta d))$ d是下降的负梯度方向。
精确的线性搜索会使得$(d^T g = 0)$,g是搜索到的最佳位置,函数f的梯度,要么g=0,要么互相垂直!
减少 zig-zag 的方法,动量方法 momentum ($(\theta_k - \theta_{k-1})$)。heavy ball method
$$
\theta_{k+1} = \theta_k - \eta_k g_k + \mu_k (\theta_k - \theta_{k-1}) \\
0 \le \mu_k \le 1
$$
另外一种方法是共轭梯度法,二次目标函数$(f = \theta A^T \theta)$常用在线性系统,非线性系统不常用?!
牛顿法,二阶方法,步长$(d_k = -H_k^{-1} g_k)$。要求目标函数强凸,海森矩阵才会可逆!
解决方案:直接用共轭梯度法求解最优步长$(H d = -g)$。线性方程等价于无约束优化二次规划$(1/2 || Hd + g||^2)$。
利用共轭梯度(CG),迭代到负曲率的地方停止迭代!
iteratively reweighted least squares or IRLS 优化 for 逻辑回归。
在牛顿法中,
$$
w_{k+1} = w_k - H^{-1}g_k \\
= (X^T S_k X)^{-1} X^T S_k z_k \\
z_k = Xw_k + S_k^{-1}(y-\mu_k)
$$
恰好是带权最小二乘问题 $((z - X^T w)^T S (z - X^T w))$ 的解。
拟牛顿法:BFGS,L-BFGS
MAP 估计导致正则项,高斯先验:l2正则。
多分类逻辑回归,最大熵模型
Bayesian logistic regression
需要计算 $(p(w|\mathcal{D}))$,从而得到$(p(y|x, \mathcal{D}) = p(y|x, w) p(w|\mathcal{D}))$。
问题:逻辑回归没有一个方便的共轭先验(和似然函数形式相同的分布)。
一些解决方案:MCMC,variational inference,expectation propagation(Kuss and Rasmussen 2005)
拉普拉斯近似,高斯近似:假定(对数据本身建立生成模型$( \theta => \mathcal{D} )$)后验概率为
$$
p(\theta| \mathcal{D}) = \frac{1}{Z} e^{-E(\theta)}
$$
$(E(\theta))$ 叫做能量函数,等于$( - p(\theta, \mathcal{D}) )$,而$(Z = p(\mathcal{D}))$。
利用泰勒级数,将能量函数在最低能量值$(\theta*)$附近展开到二阶项。
$$
E(\theta) \approx E(\theta*) + (\theta - \theta*)^T g + \frac{1}{2} (\theta - \theta*)^T H (\theta - \theta*)
$$
g是能量函数在最低能量位置的梯度,等于0,所以
$$
\hat{p}(\theta| \mathcal{D}) \approx \frac{1}{Z} e^{-E(\theta*)} \exp \left[ -\frac{1}{2} (\theta - \theta*)^T H (\theta - \theta*) \right] \\
= \mathcal{N}(\theta | \theta* , H^{-1}) \\
Z = p(\mathcal{D}) \approx e^{-E(\theta*)} (2\pi)^{D/2} |H|^{-1/2}
$$
最后一个式子是对边际分布的 拉普拉斯近似 ,因此,把第一个式子称作对后验概率的拉普拉斯近似(其实更应该称作 高斯近似)。
高斯近似通常是一个较好的近似,随着样本数目的增加,中心极限定理可以保证!(saddle point approximation in physics)
Drivation of BIC
利用高斯近似,边际分布的对数似然函数为(去掉不相关常数):
$$
p(\mathcal{D}) \approx \log p(\mathcal{D}|\theta^* ) + \log p(\theta^*) - \frac{1}{2} \log |H|
$$
$( p(\mathcal{D}|\theta^* ) )$ 常称作 Occam factor,用作模型复杂度的度量,如果假定均匀分布先验,即$( p(\theta^) \varpropto 1 )$,那么可以简化为极大似然估计,可以用MLE的值$( \hat{\theta} )$替换$( \theta^* )$。
对于第三项,有 $( H = \sum_i H_i, H_i = \nabla \nabla \log p(\mathcal{D}_i | \theta) )$,
假定每个$( H_i = \hat{H} )$,是一个常数矩阵(此时样本分布是什么情况?),那么
$$
\log |H| = \log |N \hat{H}| = \log (N^D \hat{H}) \\
= D \log N + \log |\hat{H}|
$$
其中$(D)$是参数空间的维度,H是满秩的。最后一项与N无关,可以作为常数丢弃!那么可得BIC score
$$
\log p(\mathcal{D}) = \log p(\mathcal{D}|\hat{\theta}) - \frac{D}{2} \log N
$$
高斯近似
近似先验 $( p(w) = \mathcal{N}(0, V_0) )$,后验概率为
$$
p(w | \mathcal{D}) \approx \mathcal{N}(w|\hat{w}, H^{-1})
$$
其中$(\hat{w})$是极大似然估计值,$( \hat{w} = \arg \min_w E(w) )$,$( E(w) = - \log p(\mathcal{D} | w) - \log p(w) )$。
而 $(H = \nabla \nabla E(w) |_{w^*})$。
也就是说我们之前用极大似然估计出来的参数,是参数后验分布的期望值!
当数据是线性可分的情况下,极大似然估计的模型参数$(w)$将可以是任意大的向量!sigmoid函数就变成了阶跃函数!
后验预测
没有正则项的预测$(p(y|x, \hat{w}))$是对参数的极大似然估计。
带正则项的预测$(p(y|x, \hat{w}))$ 是对参数的最大后验轨迹。
这两者预测出来的数值都只是在一个参数点的条件概率!!
这个点可以是极大似然估计出来的,也可以是最大后验估计出来的!
如果要得到在数据集上的后验概率,需要计算
$$
p(y| x, \mathcal{D}) = \int p(y|x,w) p(w| \mathcal{D}) dw
$$
但是,这个积分没难以求解,一个简单的近似是用w的 后验均值!
$$
p(y| x, \mathcal{D}) \approx p(y| x, \mathbb{E}[w])
$$
$(\mathbb{E}[w])$称作贝叶斯点!
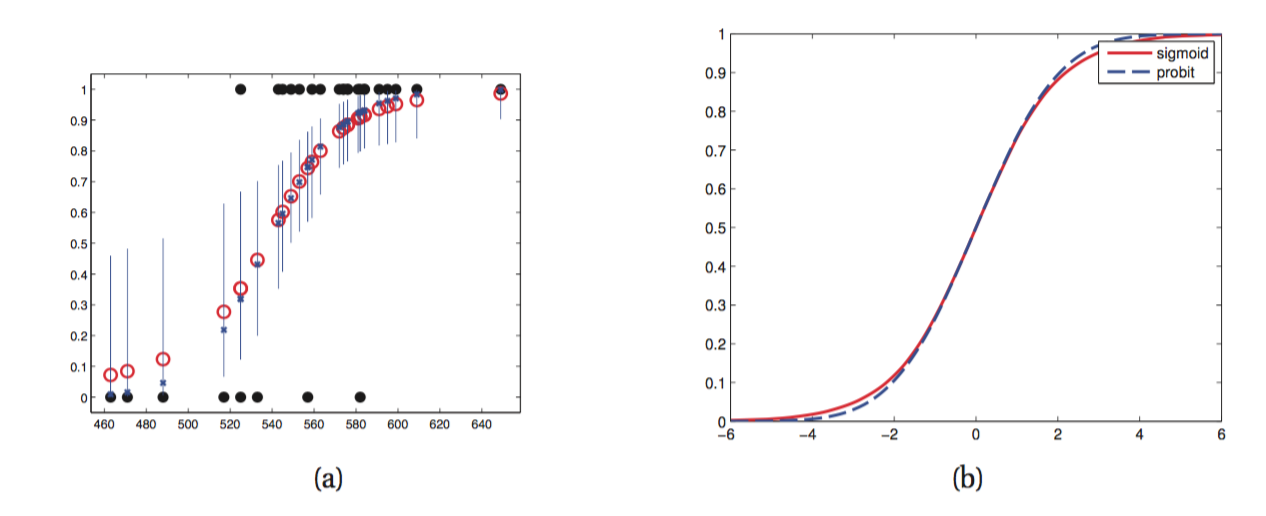
蒙特卡洛近似,即随机采样一些w,近似积分!
$$
p(y=1| x, \mathcal{D}) \approx \frac{1}{S} \sum_{s=1}^S sigm((w^s)^T x)
$$
$(w^s \sim p(w|\mathcal{D}))$ 采样自后验分布!高斯近似下,就相当于采样高斯分布!
采样多个样本时,不但可以得到较好的概率估计值,可以得到输出概率的置信区间!!!
probit 近似 当w的后验分布用高斯近似$(\mathcal{N}(w|m_N, V_N))$时,可以
$$
p(y=1| x, \mathcal{D}) \approx \int sigm(w^T x) p(w|\mathcal{D}) dw \\
= \int sigm(a) \mathcal{N}(a|\mu_a, \sigma_a^2) \\
a = w^T x \\
\mu_a = \mathbb{E}[a] = m_N^T x \\
\sigma_a^2 = x^T V_N x.
$$
将sigmoid函数用probit函数近似,probit函数是标准正态分布的累积分布函数!
和sigmoid函数非常接近,见上图!
采用这种近似后,前述积分可以得到解析表达式!
$$
\int sigm(a) \mathcal{N}(a|\mu_a, \sigma_a^2) \approx sigm(k(\sigma^2)\mu) \\
k(\sigma^2) = (1+\pi \sigma^2/8)^{-\frac{1}{2}}.
$$
此时,由于k小于1,因此相当于在极大似然估计的概率上,在横轴进行缩放!通过$(\sigma)$控制过拟合?!
但是判决面并没有变!
Residul analysis(outlier detection)
在回归问题中,计算残差$(r_i = y_i - \hat{y_i})$,其中模型估计值$(\hat{y_i} = \hat{w}^T x_i)$.
该残差应该服从正态分布$(\mathcal{N}(0, \sigma^2))$,从而可以通过 qq-plot 得到离异值?!
分类问题可以采用另外的方法!
Online learning
广义线性模型和指数族 GLM
指数族分布
指数族分布:高斯,Bernoulli, gamma分布等!
非指数族例子:Student t 分布, 均匀分布
重要性:
- finite-sized sucient statistics.
under certain regularity conditions, the exponential family is the only family of distributions with finite-sized sucient statistics, meaning that we can compress the data into a fixed-sized summary without loss of information. This is particularly useful for online learning, as we will see later.
-
唯一存在共轭先验的分布族
-
least set of assumptions
The exponential family can be shown to be the family of distributions that makes the least set of assumptions subject to some user-chosen constraint
定义
概率密度函数
$$
p(x) = h(x) \exp(\theta^T \phi(x) - A(\theta)) \\
= \frac{1}{Z(\theta)}h(x) e^{\theta^T \phi(x)}
$$
$(Z)$是归一化因子,$(A)$是对数归一化因子,$(\theta)$被称作自然参数。
$(\phi(x) \in \mathcal{R}^d)$被称为充分统计向量(vector of sucient statistics)。
如果$(\phi(x)=x)$,称为自然指数族。$(\theta \rightarrow \eta(\theta))$。
Log partition function 性质:
- $(A(\theta))$的一阶导是$(\phi(x))$的期望,而二阶导是其协方差矩阵!即对数矩母函数!
极大似然估计
N个iid的样本的对数似然函数为:
$$
l(\theta) = \theta^T \sum_i \phi(x_i) - N A(\theta) + constant
$$
第一项是$(\theta)$的线性函数,第二项由于其二阶导是协方差矩阵,非负,所以也为凸函数,因此指数族N个独立同分布样本的对数似然函数为凸函数,
因而通过极大似然估计参数,可以很容易得到最优解!并且由
$$
\nabla_{\theta} l = 0 \\
\nabla_{\theta} A = E \phi(X)
$$
可得期望匹配条件
$$
E \phi(X) = \frac{1}{N} \sum_i \phi(x_i)
$$
例如对 Bernoulli 分布样本,$(\phi(X)= \mathbb{I}(X=1))$,因此要求模型预测的期望值要和样本均值相同!
Pitman-Koopman-Darmois theorem 理论:在一些约束下,指数族是为一个分布族,其充分统计量是有限的(不随样本个数增加而增加)!
例如这里充分统计量数目不随N增长,一直为 N 和 $(\sum_i \phi(x_i))$!
贝叶斯统计
似然函数具有如下形式:
$$
p(\mathcal{D}|\theta) \varpropto g(\theta)^N \exp(\eta(\theta)^T s_N)
$$
这里$(s_N)$是N个样本之和,而在canonical parameters形式下为:
$$
p(\mathcal{D}|\eta) \varpropto g(\eta)^N \exp(N \eta^T \bar{s} - N A(\eta))
$$
选择共轭先验与似然函数具有相同的形式,将会使得贝叶斯分析简化,指数族是唯一具有这种性质的分布族!(不是因为封闭形式的原因么?)
$$
p(\eta|v_0, \bar{\tau_0}) \varpropto g(\eta)^N \exp(v_0 \eta^T \bar{\tau_0} - v_0 A(\eta))
$$
那么后验分布将为
$$
p(\theta|\mathcal{D}) = p(\theta| v_0 +N , \tau_0 + s_N) \\
p(\eta|\mathcal{D}) = p(\eta| v_0 +N , \frac{v_0 \bar{\tau_0} + N \bar{s}}{v_0 + N})
$$
最大熵原理
最大熵原理是说,要选择分布使得熵最大,在约束条件:对一些特殊函数(特征)期望值和样本均值相同!
$$
\max -\sum_x p(x) \log(p(x)) \\
s.t. \sum_x f_k(x)p(x) = F_k, k=1,...,m \\
\sum_x p(x)=1
$$
利用拉格朗日对偶,及KKT条件,易知分布要满足
$$
p(x) = \frac{1}{Z} \exp(\lambda_k f_k(x))
$$
最大熵分布是指数族分布!!这个分布也叫 Gibbs 分布!
广义线性模型 GLM
GLM:均值函数是输入的线性组合,然后加上一个非线性变换!输出是指数族分布的模型!
设标量响应变量满足分布:
$$
p(y_i| \theta, \sigma^2) = \exp \left[\frac{y_i \theta - A(\theta)}{\sigma^2} + c(y_i, \sigma^2) \right]
$$
$(\theta)$是自然参数,$(\sigma)$是dispersion parameter(通常是1),A是 partition function 和指数族里面的 A 一样!
例子,逻辑回归自然参数是对数发生比 $(\theta = \log \frac{\mu}{1-\mu})$,其中均值$(\mu = \mathbb{E}y=p(y=1))$。
均值到自然参数的转换函数$(\phi)$被指数族分布函数形式唯一确定。
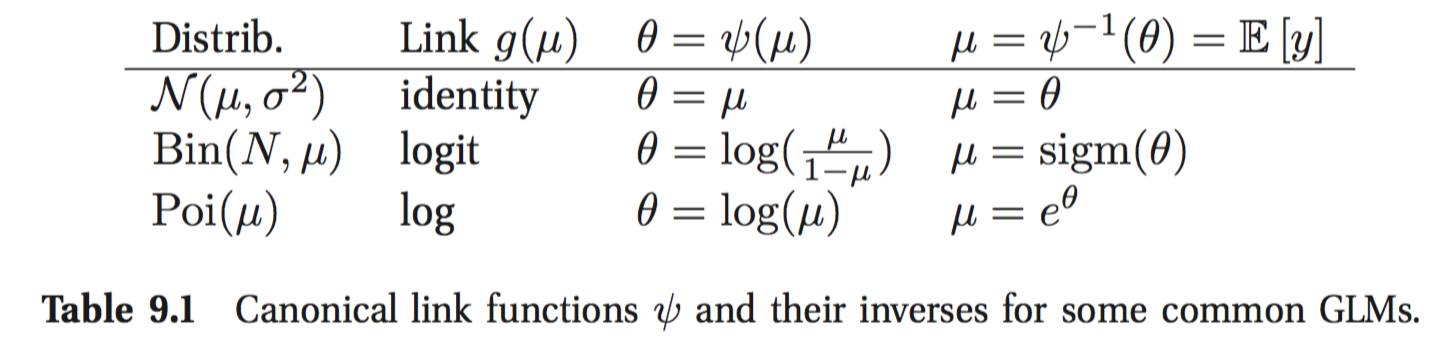
这个转换函数的逆函数$(\mu = \phi^{-1}(\theta) = A'(\theta))$。
该值是输入的线性变化加上一个非线性变换$(g^{-1})$!
$$
\mu_i = g^{-1}(\eta_i) = g^{-1}(w^T x_i)
$$
该非线性变化也叫均值函数,其反函数$(g)$称作 link function! 例如在逻辑回归中均值函数就是sigmoid函数!
均值函数的一种选取方式是$(g=\phi)$,得到canonical link function,此时自然参数就是输入的线性组合$(\theta_i = w^T x_i)$!
从而
$$
p(y_i| \theta, w, \sigma^2) = \exp \left[\frac{y_i w^T x_i - A(w^T x_i)}{\sigma^2} + c(y_i, \sigma^2) \right]
$$
例子:
- 线性回归,$(y_i \in \mathbb{R}, \theta_i = \mu_i = w^T x_i, A(\theta)=\theta^2/2)$
- binomial回归,$(y_i\in{0,1,...,N_i}, \pi_i = sigm(w^T x_i), \theta = \log(\pi_i / (1-\pi_i)) = w^T x)$
- 泊松回归,$(y_i \in \mathcal{N}^+, \mu_i = exp(\theta), \theta=w^T x)$
$$
\mathbb{E}[y|x,w,\sigma^2] = \mu_i = A'(\theta) \\
Var[y|x,w,\sigma^2] = \sigma_i^2 = \sigma^2 A''(\theta) \\
$$
极大似然估计和最大后验估计
对数似然函数为为:
$$
l(w) = \log p(\mathcal{D}|w) = \frac{1}{\sigma^2}\sum_{i=1}^N l_i \\
l_i = \theta_i y_i - A(\theta_i)
$$
当使用 canonical link 函数时,对数似然函数的梯度为:
$$
\nabla_w l = \frac{1}{\sigma^2} \sum_{i=1}^N (y_i - \mu_i) x_i
$$
他是用误差对样本加权,然后求和得到!上式为0的时候,就是最大熵方法的约束条件:特征的经验均值和期望值相等!
嗨森矩阵为:
$$
H = X^T S X \\
S = diag\{... \frac{d\mu_i}{d\theta_i} ...\}
$$
Fisher scoring method?
带高斯先验的最大后验相当于增加了l2正则项!
Probit regression
将逻辑回归里面的sigmoid函数换成一般的函数:$(f: \mathbb{R} \rightarrow [0,1])$
而均值函数$(g^{-1} = \Phi)$是标准正态cdf。这个函数跟sigmoid函数很像,都是S型函数!

隐变量解释:设存在两个隐变量$(u_{0,i}, u_{1,i})$,随机选择模型
$$
u_{0,i} = w_0 ^T x_i + \delta_{0,i} \\
u_{1,i} = w_1 ^T x_i + \delta_{1,i} \\
y_i = \mathbb{I}(u_{1,i} > u_{0,i})
$$
对两隐变量作差,可得差分随机选择模型,令$(\epsilon_i = \delta_{1,i} - \delta_{0,i})$,且假定服从标准正态分布
$$
p(y_i=1|x_i, w) = \Phi(w^T x_i)
$$
推广到有序的 probit 回归,响应变量是多个且有序的情况下!
Multinomial probit models:直接看模型数学公式
$$
z_{ic} = w^T x_{ic} + \epsilon_{ic} \\
\epsilon \sim \mathcal{N}(0, R) \\
y_i = \arg \max_c z_{ic}
$$
Multi-task learning
如果不同任务的输入相同,目标相关的情况下,可以同时训练这几个模型,同时优化参数,可以得到更好的性能!
- multi-task learning (Caruana 1998)
- transfer learning (e.g., (Raina et al. 2005))
- learning to learn (Thrun and Pratt 1997)
Hierarchical Bayes for multi-task learning:
设响应变量为$(y_{ij})$,i为样本指标,j为任务指标,关联的特征向量为$(x_{ij})$。
用GLM建模 $(\mathbb{E}[y_{ij}|x_{ij}] = g(x_{ij}^T \beta_j))$。
由于有多个任务需要多个$(\beta)$。
可以单独训练每一个模型,但在实际问题中,比如商品偏好模型,由于长尾分布的原因,某些商品数据很多,而其他的很少!
对于数据少的模型,训练很困难。可以通过隐变量,让这些数据共享!
具体做法是控制模型参数的先验分布:$(\beta_j \sim \mathcal{N}(\beta_*, \sigma_j^2 I), \beta_* \sim \mathcal{N}(\mu, \sigma_*^2 I))$
每个模型的参数通过先验分布参数$(\beta_*)$联系到一起。
可以通过交叉验证选取$(\mu, \sigma_j, \sigma_*)$。
案例:个性化垃圾邮件过滤
对每一个用户需要训练一个模型参数$(\beta_j)$,但由于用户标记通常很少,因此难以单独训练,可以采用 multi-task learning。
$$
\mathbb{E}[y_i | x_i, u=j] = (\beta_*^T + w_j)^T x_i
$$
这里$(w_j = \beta_j - \beta_*)$用来估计个性化的部分!
Learn to rank
查询q和文档d的相关性,标准方法:bag of word 概率语言模型(这不是朴素贝叶斯吗?)
$$
sim(q, d) = p(q | d) = \Pi_{i=1}^n p(q|q_i)
$$
The pointwise approach: 对每一个q和文档d,生成一个特征向量$(x(q, d))$,
学习模型$(p(y=1| x(q,d)))$,用概率进行排序。
pairwise: 学习 $(p(y_{jk}=1| x(q, d_j), x(q, d_k)))$,$(y_{jk}=1)$表示文档j相关度大于文档k相关度,
一种建模方法是:
$$
p(y_{jk}=1| x(q, d_j), x(q, d_k)) = sigm(x(q, d_j) - x(q, d_k))
$$
关键工作:RankNet (Burges et al. 2005)
好处,人比较两个文档哪个更相关比打分更容易,因而标注数据准确性更高?
The listwise approach:学习一个排列$(\pi)$。分布
$$
p(\pi|s) = \Pi_{j=1}^m \frac{s_j}{\sum_{u=j}^m s_n}
$$
$(s_j = s(\pi^{-1}(j)))$ 是文档排列在第j个位置的时候的score!
例如$(\pi = (A, B, C))$,那么排列的概率为A排在第一的概率乘以B排在第二的概率乘以C排在第三的概率
$$
p(\pi|s) = \frac{s_A}{s_A+s_B+s_C} \times \frac{s_B}{s_B+s_C} \times \frac{s_C}{s_C}
$$
而这个score可以通过模型学习$(s(d) = f(x(q, d)))$,通常取为线性模型$(w^T x)$。
ListNet Cao et al. 2007
Latent linear models
因子分析
实值隐变量 $(z_i \in \mathbb{R}^L)$,其先验分布假设为高斯(后面会假设为其他分布)
$$
p(z_i) = \mathcal{N}(z_i | \mu_0, \Sigma_0)
$$
观测变量 $(x_i \in \mathbb{R}^D)$,假设其服从高斯分布,其均值是隐变量的线性函数!
$$
p(x_i | z_i, \theta) = \mathbb{N}(W z_i + \mu, \Phi)
$$
W 被称为 factor loading matrix, 而应变量称为因子,被强制要求为能够解释观测变量之间的相关性,此时$(\Phi)$是对角的!
一个特例是$(\Phi = \sigma^2 I)$,为 Probabilistic Principal Components Analysis。
- 因子分析作为协方差的低秩矩阵分解
边际分布
$$
p(x_i | \theta) = \mathbb{N}(x_i | W\mu_0 + \mu,\Phi + W\Sigma_0 W^T)
$$
不是一般性,可以假设$(\mu_0 = 0, \Sigma_0 = 1)$,一般情况可以作变量代换得到这种形式,即要求隐变量z是标准正态分布,且独立同分布。
因此可得协方差矩阵为
$$
\text{Cov}(x) = W W^T + \Phi
$$
从上式可以看到,因子分析只使用了 O(LD + D)个参数,$(\Phi)$ 是对角的!
因子分析的目的是为了通过隐变量z得到有用的信息,其后验分布为
$$
p(z_i| x_i, \theta) = \mathcal{N}(z_i | m_i, \Sigma_i) \\
\Sigma_i = (\Sigma_0 + W^T \Phi^{-1} W)^{-1} \\
m_i = \Sigma_i(W^T \Phi^{-1} (x_i - \mu) + \Sigma_0^{-1} \mu_0)
$$
m 被称作隐因子 or latent score.
W不是唯一的!! 例如可以通过做一个正交变换R,RW 仍然是有效的!解决方法,增加约束。
- 要求W是正交的,然后按照 latent factor 的方差排序: PCA
- 要求W是下三角,即每个观测变量只与前面的因子有关
- 稀疏约束:l1 regularization (Zou et al. 2006), ARD (Bishop 1999; Archambeau and Bach 2008), or spike-and-slab priors (Rattray et al. 2009).
- Choosing an informative rotation matrix. varimax
- 非高斯先验 for 隐变量:ICA
因子旋转: http://www.cis.pku.edu.cn/faculty/vision/zlin/Courses/DA/DA-Class7.pdf
混合因子分析 (Hinton et al. 1997)
因子模型假设数据是嵌入在低维线性流形之中!而实际上大多数时候是曲线流形!
曲线流形可以通过分片线性流行近似。
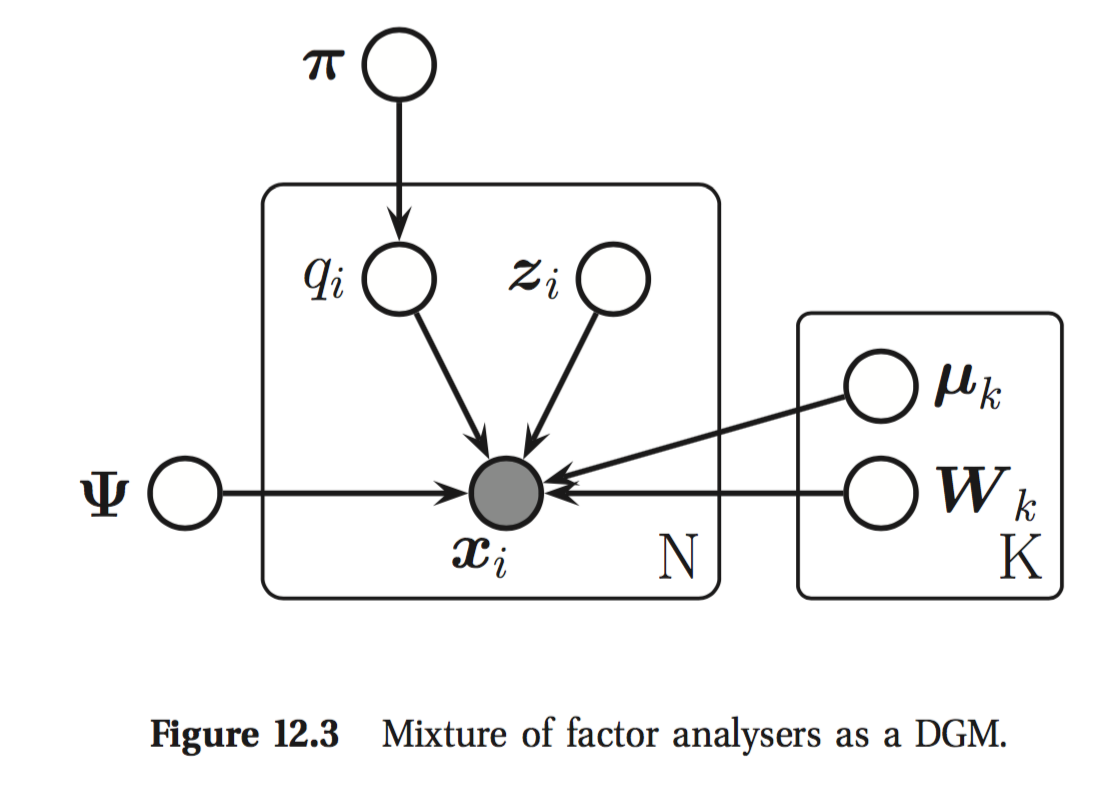
有K个FA模型,对应维度为$(L_k)$,参数$(W_k)$,
隐变量 $(q_i \in \{1,2,...,K\})$。
$$
p(x_i| z_i, q_i = k, \theta) = \mathcal{N}(x_i | \mu_k + W_k z_i, \Phi) \\
p(z_i| \theta) = \mathcal{N}(z_i| 0, I) \\
p(q_i| \theta) = \text{Cat}(q_i| \pi)
$$
因子分析的EM算法
在E步,根据当前的参数,对每一个数据计算它来自cat c的概率:
$$
r_{ic} = p(q_i=c| x_i, \theta) \propto \pi_{c} \mathcal{N}(x_i|\mu_c, W_cW_c^T + \Phi) \\
$$
在M步,利用E步估计的c,可以分别计算出每个cat的参数$(\mu_c, W_c)$,以及新的$(\pi_{c})$。
PCA
(Tipping and Bishop 1999): 当 $(\Phi = \sigma^2 I)$ 并且 W 矩阵是正交的,随着$(\sigma^2 \rightarrow 0)$,
模型就变为principal components analysis(PCA, KL变化)了!$(sigma^2 >0 )$的版本成为概率PCA(PPCA)。
Classical PCA
最小化重构误差
$$
\min J(W, Z) = \sum_{i=1}^N || x_i - \hat{x_i}||^2 = || X - WZ^T ||^2_F \\
s.t. W^T W = I_L .
$$
F表示Frobenius范数。
SVD
略:truncated SVD
PPCA (Tipping and Bishop 1999)
因子模型中,当 $(\Phi = \sigma^2 I)$,并且W为正交阵,那么观测数据的对数似然函数为
$$
\log p(X| W, \sigma^2) &= - \frac{N}{2} \log |C| - \frac{1}{2} \sum_{i=1}^N x_i^T C^{-1} x_i \\
&= - \frac{N}{2} \log |C| - \frac{1}{2}
$$