GAN

论文：Generative Adversarial Nets，an J. Goodfellow, Jean Pouget-Abadie∗, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair†, Aaron Courville, Yoshua Bengio‡，2014

• 生成模型G，对于随机noise z，分布$(p_z(z))$，生成一个样本 $(G(z; \theta_g))$
• 判别模型D，是一个常规的二分类模型，输出是样本来自真实数据的概率，$(D(x; \theta_d))$
• 极大似然估计，来自样本的认为是正例，来自生成模型的认为是负例
• minmax value function $(V(D, G))$

$$
\min_G \max_D V(D, G) = \mathbf{E} _ {x \in p_{data}(x)}[\log D(x)] + \mathbf{E} _ {x \in p_{z}(z)}[\log(1-D(G(z)))]
$$

训练算法：

理论结论

• 全局最优：$(p_g = p_{data})$
• 对固定的G，

$$
V(G,D) = \int_x dx p_{data}(x) \log(D(x)) + p_g(x) \log(1 - D(x))
$$

容易验证，最优的D满足

$$
D^* _ G(x) = \frac{p_{data}(x)}{p_{data}(x) + p_g(x)}
$$

最优 value function为

$$
C(G) = \mathbf{E} _ {x \in p_{data}(x)}[\log \frac{p_{data}(x)}{p_{data}(x) + p_g(x)}] + \mathbf{E} _ {x \in p_{z}(z)}[\log(\frac{p_{g}(x)}{p_{data}(x) + p_g(x)})] \\
= - \log 4 + 2 JSD(p_{data} || p_g)
$$

JSD 是 Jensen–Shannon divergence. 上式最优的结果是 $(-\log4)$，当 $(p_g = p_{data})$ 取得。

• 算法 Algorithm 1 的收敛性,结论是:如果G和D有足够的容量(可以拟合任意函数),那么算法1可以保证$(p_g)$收敛到$(p_{data})$

DCGAN

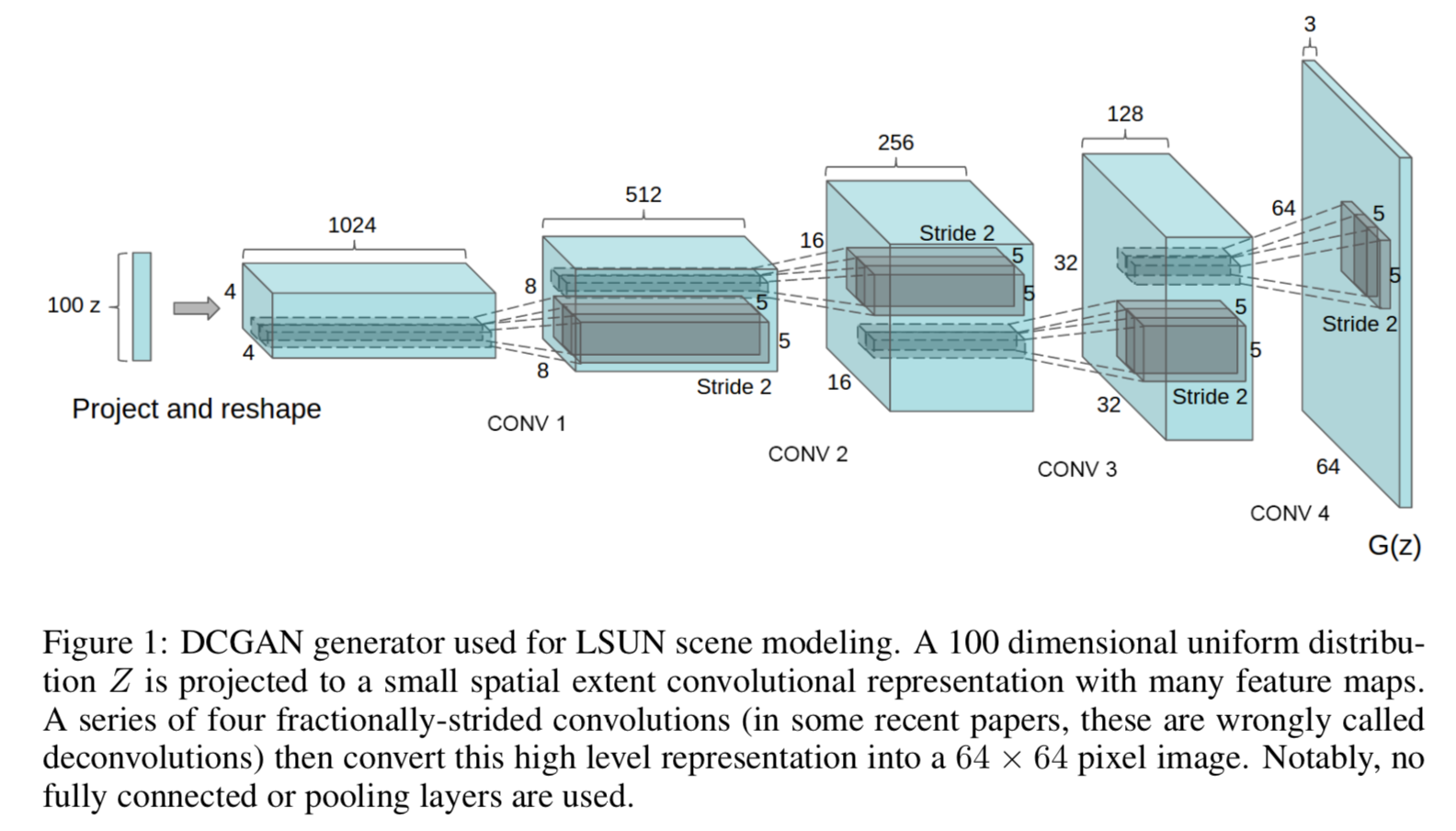
• 论文: Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks
• 通过GAN进行无监督学习, 学习到图像的层级的特征表示
• 将GAN 的一部分作为特征抽取器用于监督学习的任务
• 贡献:
  1. 对模型结构做了一些约束,使得模型在大多数情况下都能稳定的快速收敛
  2. 生成器的算术性质

生成自然图像

• 之前生成的自然图像都比较模糊
• LAPGAN
• 几个技巧:
  1. 将全连接层去掉不要
  2. 用 strided convolution 替换Pooling操作

• 图像去重: 3072-128-3072 de-noising dropout regularized RELU autoencoder on 32x32 downsampled center-crops of training examples. 得到编码后,二值化作为hash值,用于去重。
• 图像算术, 对输入空间Z进行算术运算, 运算的结果再通过生成模型生成图像。

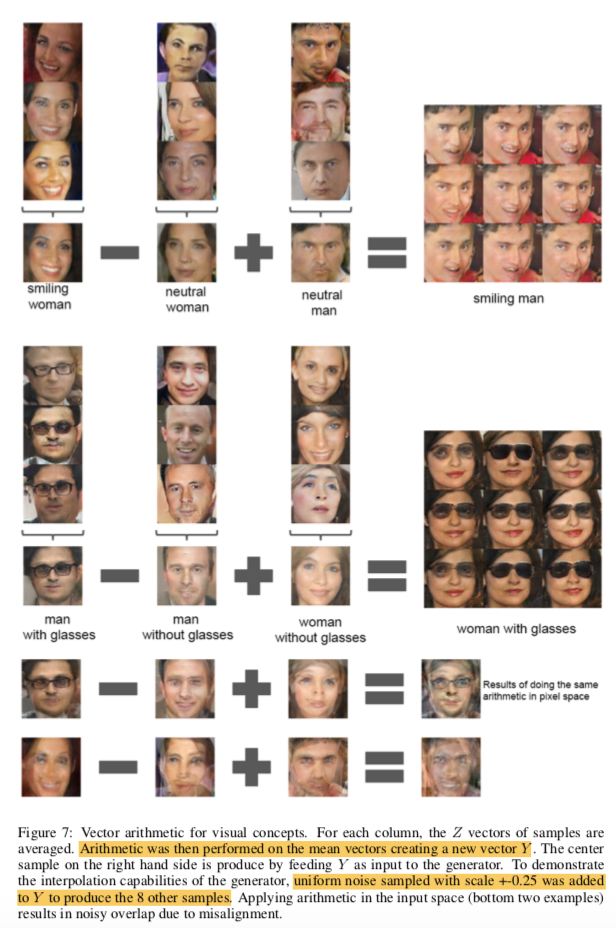
VAE-GAN

UNsupervised Image-to-image Translation Networks

训练技巧2016

• 论文: Improved Techniques for Training GANs
• 代码: https://github.com/openai/improved-gan
• GAN与纳什均衡的关系?
• 梯度交替优化的问题: 比如优化目标是 xy, 第一个player可以修改x,目标是使xy尽可能大, 第二个player可以修改y,目标是使xy尽可能小。均衡解是 x=y=0, 但是基于梯度优化的会不收敛。
• 特征匹配: 让判别器的中间层的特征的期望值,在真实数据和生成器生成的数据中,尽可能相同
  • 新目标函数 $(||E_{x \in p_{data}f(x) - E_{z \in p_{z}} f(G(z))}||)$ 其中f代表每个网络中间的某个神经元的输出
• GAN模型折叠, 总是输出一个固定的结果, 我还真碰到过
• 标签平滑, 用0.1,0.9代替0和1作为标签, 可以减少对抗样本的漏洞, 但是会使得p_data为0的区域不为0, 所以作者认为用单边平滑,只讲1用一个小于1的数替代

• virtual batch normalization, 不是基于当前batch的统计信息,而是用一个固定的batch??

• 半监督学习

  • 以K分类的MNIST数据集为例,将生成模型生成的样本的标签作为K+1, 这样交叉熵损失函数就可以分解为K类的交叉熵损失函数和GAN的判别模型损失函数之和。

CGAN2014

• 基于label生成,而不是随意生成
• D(x) 替换成 D(x|y), G(z) 替换成 G(z|y)

def discriminator(x, y):
    inputs = tf.concat(axis=1, values=[x, y])
    D_h1 = tf.nn.relu(tf.matmul(inputs, D_W1) + D_b1)
    D_logit = tf.matmul(D_h1, D_W2) + D_b2
    D_prob = tf.nn.sigmoid(D_logit)

    return D_prob, D_logit

def generator(z, y):
    inputs = tf.concat(axis=1, values=[z, y])
    G_h1 = tf.nn.relu(tf.matmul(inputs, G_W1) + G_b1)
    G_log_prob = tf.matmul(G_h1, G_W2) + G_b2
    G_prob = tf.nn.sigmoid(G_log_prob)

    return G_prob

Image-to-image translation with conditional adversarial nets(pix2pix)

• 伯克利AI实验室
• 损失函数, x是草图, z是随机噪声, y是真实的图像
  $$
  L_{cGAN}(G, D) = E_{x,y}[log D(x, y)] + E_{x, z}[1 - log D(x, G(z))]
  $$

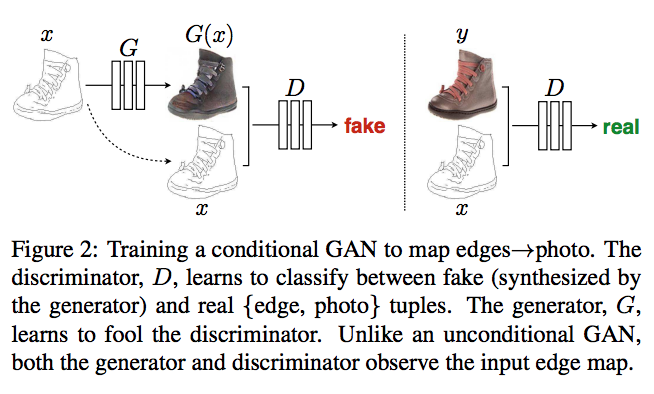
• 在GAN损失函数的基础上,加上L1损失函数可以帮助减少模糊。需要将x和y关联起来,x是草图,y是groundtruth,z是采样值,为啥还要z?不直接训练{x, y},用L1损失函数就行。
• 解释: GAN损失函数可以让模型更具泛化能力,相当于一种正则

GAN单图像超分辨 SRGAN

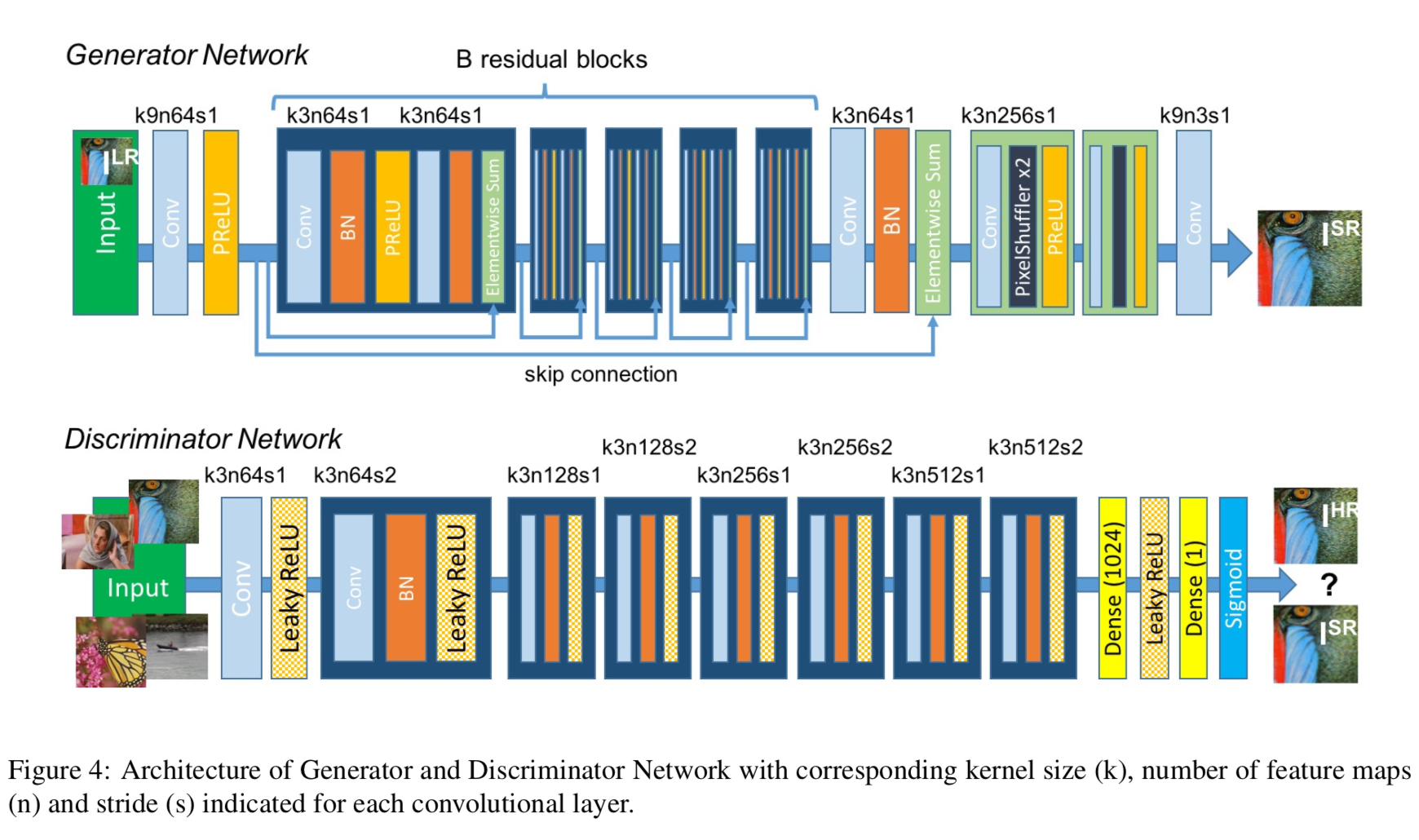
• Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network
• 重新设计了损失函数,低分辨图像通过生成网络G后的输出与groundtruth之间的损失函数
• 损失函数包括内容损失和对抗损失
• 内容损失不但包括了在图像空间中的MSE,还包括了在VGG不同特征层上了MSE
• 对抗损失主要是G生成的高清图像的对数损失 - log[D(G(I_LR))]

Hing loss

参考

• Generative Adversarial Networks (GANs), Ian Goodfellow, OpenAI Research Scientist NIPS 2016 tutorial
• Introduction to GANs, Ian Goodfellow, Staff Research Scientist, Google Brain, CVPR Tutorial on GANs