摘要
- 在线预估的两个重要的任务
- tabular input space
- online data generation
- GBDT和NN都有自己的弱点
- GBDT弱点在于sparse特征
- NN弱点在于dense特征
- DeepGBM两个模块
- CatNN 处理sparse特征的NN
- GBDT2NN 处理dense特征, 将GBDT中学到的知识、特征重要性、特征分割点等知识蒸馏到NN中
- GBDT的两个问题
- 不能做online learning, 也意味着难以处理极大规模的训练数据
- 对(高度)稀疏特征难以拟合得很好。因为分裂是根据特征的统计信息,而稀疏特征onehot之后,分裂对单个特征的统计信息的变化很小,所以难以拟合的很好。一些解决的方法,将sparse特征通过一些编码方法变成连续特征。但每一种编码方法都有其局限性,无法充分表示原有特征中的信息量。
- sklearn的一个编码库 https://github.com/scikit-learn-contrib/categorical-encoding
- onehot之后的统计信息还有偏? LightGBM
- NN的问题
- dense特征拟合效果通常不如GBDT,原因是局部最优。我认为还有模型结构的限制也是一个原因,因为dense特征要拟合好需要高度非线性,那么需要很深的NN,而这导致优化更加困难
相关工作
- GBDT在线学习方法
- XGBoost、LightGBM 固定树结构,改变叶子节点的权重
- GBDT处理sparse特征
- CatBoost, 通过target statistic信息将sparse特征编码成连续值特征
- 深度GBDT
- 周志华的两篇文章,DeepForest和mGBDT,将树模型多层堆叠起来
- DNN处理连续特征
- 归一化、正则
- 离散化: Supervised and unsupervised discretization of continuous features
- DNN与GBDT结合的工作
- Facebook将GBDT的叶子节点作为sparse特征
- Microsoft用GBDT学习NN的残差
DeepGBM
- CatNN sparse特征, 目前主流的DNN都可以使用,没有限制
- GDBT2NN dense 特征
- 树的特征选择信息。用$(I^t)$表示第t棵树的特征选择向量,即第k个元素为1表示第k个特征被第t棵树选择用于构建决策树。然后只是用这些选出来的特征$(x(I^t))$来构建NN
- 树结构蒸馏。训练一个神经网络,用$(x(I^t))$作为输入特征,用决策树的输出叶子节点ID作为target。$(\theta)$是NN的参数,$(L^{t,i})$表示原始训练数据中第i个样本被第t棵树分到的叶子节点ID的onehot编码, L是交叉熵损失函数
$$
\min_{\theta} \frac{1}{n}\sum_{i=1}^n L(NN(x^i[I^t]; \theta), L^{t,i})
$$ - 叶子节点输出。叶子节点输出向量$(q^t)$不用学习,直接映射即可。最终决策树输出为
$$
y^t(x) = NN(x[I^t]; \theta) \times q^t
$$ - 多棵树的蒸馏, 直接用多个NN来拟合多个树太低效了
- leaf embedding 蒸馏, $(p^{t,i})$ 是预测值,直接用一个NN将leaf id映射到预测值,从而得到leaf embedding向量$(H^{t,i}=H(L^{t,i}; w^t))$。这样一来也可以将树结构蒸馏的target改为$(H^{t,i})$
$$
\min_{w,w_0,w^t} \frac{1}{n}\sum_{i=1}^n L(w^TH(L^{t,i}; w^t) + w_0, p^{t,i}) \\
\min_{\theta} \frac{1}{n}\sum_{i=1}^n L(NN(x^i[I^t]; \theta), H^{t,i})
$$ - tree grouping: 从一组tree中做蒸馏
- 如何分组: 随机均匀分组、根据重要性均匀分组etc,文中使用随机,目测差异不会很大
- 如何蒸馏: 输入由单棵树的叶子id onehot值$(L^{t})$变成多个树的concat, target变成多个叶子节点的和! concat之后embedding向量(相当于多个embedding向量之和)作为NN蒸馏学习的target。NN蒸馏的输入则是该组决策树用到的特征,也可以根据特征重要性取TOP。
$$
\min_{w,w_0,w^t} \frac{1}{n} \sum_{i=1}^n L(w^TH(concat_{t\in T}L^{t,i}; w^t) + w_0, \sum_{t\in T} p^{t,i}) \\
G^i = H(concat_{t\in T}L^{t,i}; w^t)
$$
- 最终GBDT2NN的输出是多个模型最终输出之和。
- leaf embedding 蒸馏, $(p^{t,i})$ 是预测值,直接用一个NN将leaf id映射到预测值,从而得到leaf embedding向量$(H^{t,i}=H(L^{t,i}; w^t))$。这样一来也可以将树结构蒸馏的target改为$(H^{t,i})$
- DeepGBM训练:
- 端到端离线训练,批量更新。首先训练一个GBDT,然后利用叶子节点id和权重训练出leaf embedding; 然后端到端训练,一方面利用leaf embedding训练一个新的NN对模型结构做蒸馏构,造出对GBDT结构蒸馏损失,另一方面利用GBDT2NN的输出与CatNN的输出加权和拟合的误差损失。相当于蒸馏结构损失作为一个辅助任务或正则项。k是决策树分组数, $(L^{T_j})$代表该分组的对leaf embedding的拟合损失。
$$
\hat{y}(x) = \sigma(w_1\times y_{GBDT2NN}(x) + w_2\times y_{cat}(x)) \\
L_{offline} = \alpha L(\hat{y}(x), y) + \beta\sum_{j=1}^{k} L^{T_j}
$$ - 在线学习: 只更新拟合误差损失部分(及上式的第一部分作为在线更新损失)。问题: 那么这种方法跟直接用GBDT叶子id作为额外的NN sparse特征的方法有什么优势?因为二者都没有更新GBDT模型
- 端到端离线训练,批量更新。首先训练一个GBDT,然后利用叶子节点id和权重训练出leaf embedding; 然后端到端训练,一方面利用leaf embedding训练一个新的NN对模型结构做蒸馏构,造出对GBDT结构蒸馏损失,另一方面利用GBDT2NN的输出与CatNN的输出加权和拟合的误差损失。相当于蒸馏结构损失作为一个辅助任务或正则项。k是决策树分组数, $(L^{T_j})$代表该分组的对leaf embedding的拟合损失。
试验结论
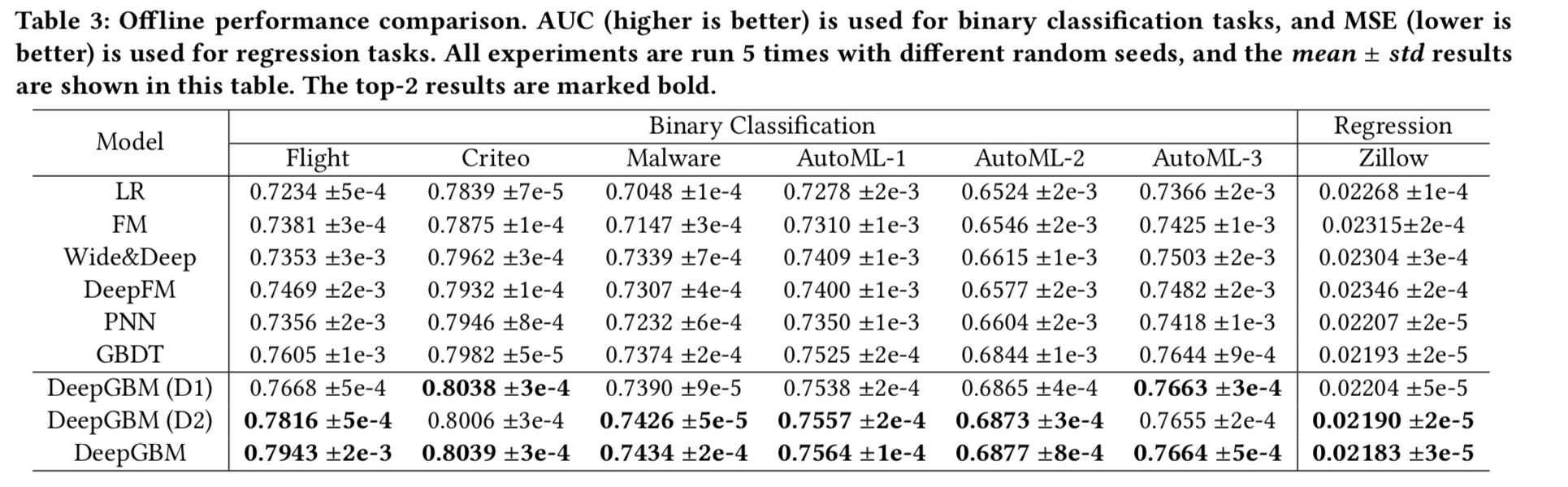
- 试验对比: D1 是直接用GBDT+NN(应该微软17年的论文方法,直接boost融合); D2 是只用GBDT2NN,没有CatNN
- 将GBDT蒸馏为NN这一步离线性能上有轻微的额外收益
- 将GBDT和NN联合训练比单独的GBDT和单独的NN有额外收益
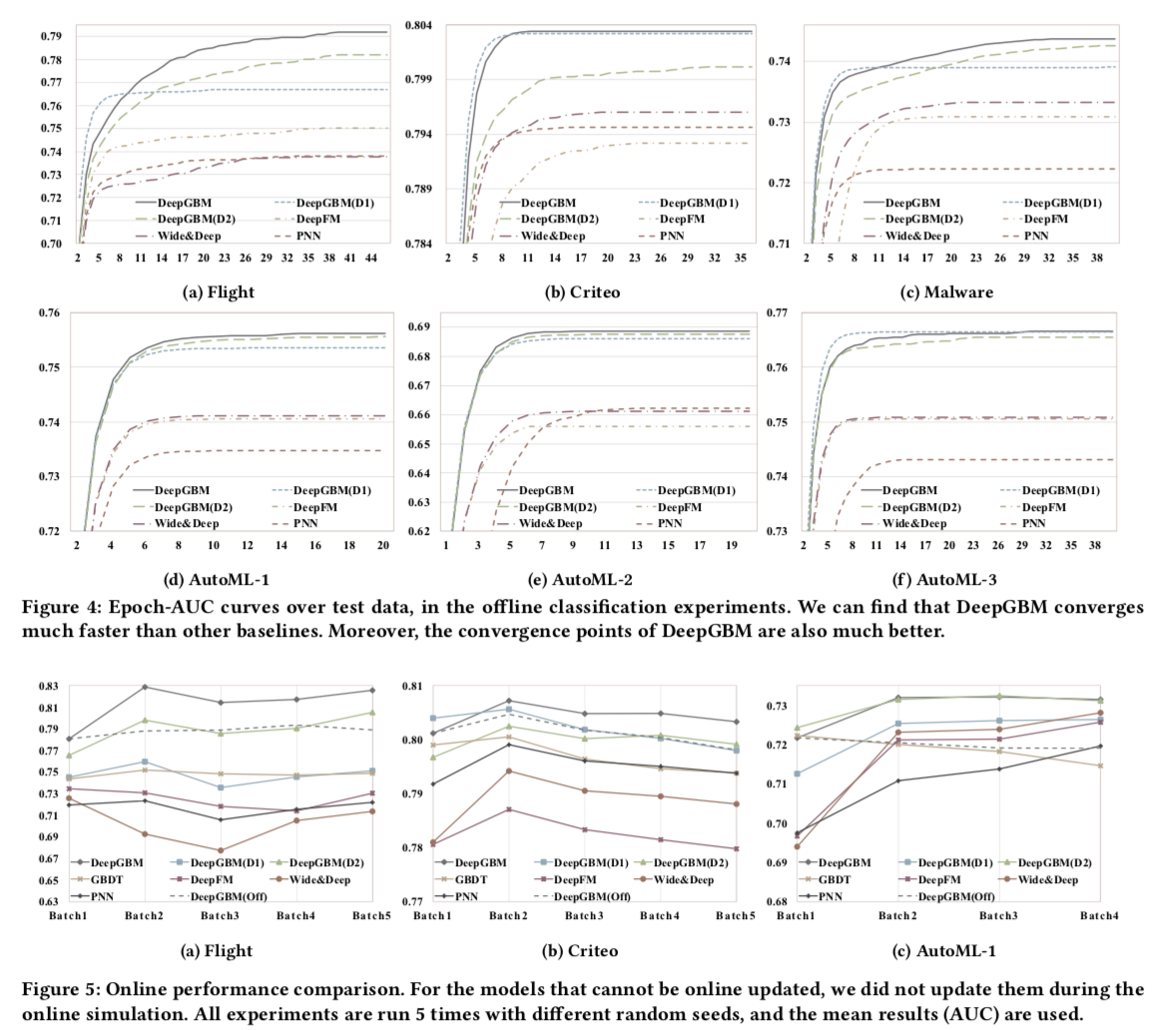
- 将GBDT蒸馏为NN这一步对在线更新上有显著收益
- 开源代码 https://github.com/motefly/DeepGBM
疑问
- 为啥FM和wide & deep在这种CTR预估数据集上的性能被采用了label encoded处理过sparse特征后的LightGBM完虐? 似乎不太符合常理?
- 个人认为这种方案还是不太方便, 有没有更好的方案, 可以让NN也能具有GBDT处理连续特征的能力?