xDeepFM: Combining Explicit and Implicit Feature Interactions for Recommender Systems

Table of Contents

关于
主要结论

关于

论文: xDeepFM: Combining Explicit and Implicit Feature Interactions for Recommender Systems
作者单位: 科大、微软

主要结论

学习特征的显式、向量级别的高阶交叉
DCN学到的是标量级的高阶交叉, 因为每一层的输出向量都是最原始输入向量的标量积, 只是这个标量系数是输入向量的高阶非线性函数
推荐系统的数据主要是 multi-field 的离散特征,假设经过embedding层之后, 得到的向量是多个embedding向量的concat的结果 $( e = [e_1, e_2, ..., e_m] )$
隐式高阶交叉: FNN, DNN 等模型,直接将上述得到的向量 e 放到MLP中,学习特征间的高阶交叉
embedding + concat 相当于对直接embedding的权重矩阵施加了自由度限制,权值矩阵的某些部分限制为0
显式高阶交叉DCN
$$
x_{k+1} = x_0 x_k^T w_{k+1} + b_k + x_0
$$
$(x_k)$是列向量, 第一项的 $(x_k^T w_{k+1})$是一个标量,相当于将上一层的向量做了个线性组合得到一个系数,重新乘以$(x_0)$, 这一项加上残差项相当于对原始输入$(x_0)$乘以了一个系数 $(x_k^T w_{k+1} + 1)$ 所以说是标量级的交叉, 而常数项(非齐次项)在迭代中的作用,相当于引入k,k-1,k-2,...,1阶交叉,否则就只有 k+1 阶项了。相比于直接的二项式, DCN的参数数目跟阶数k是线性关系,而一般多项式是k次方关系
作者认为这种DCN的交叉只实现某种特定的交叉:
- 隐层是输入的标量乘法
- 交互限制在向量的位级别, 即输入向量 x0的不同位之间通过权值向量w实现交叉??
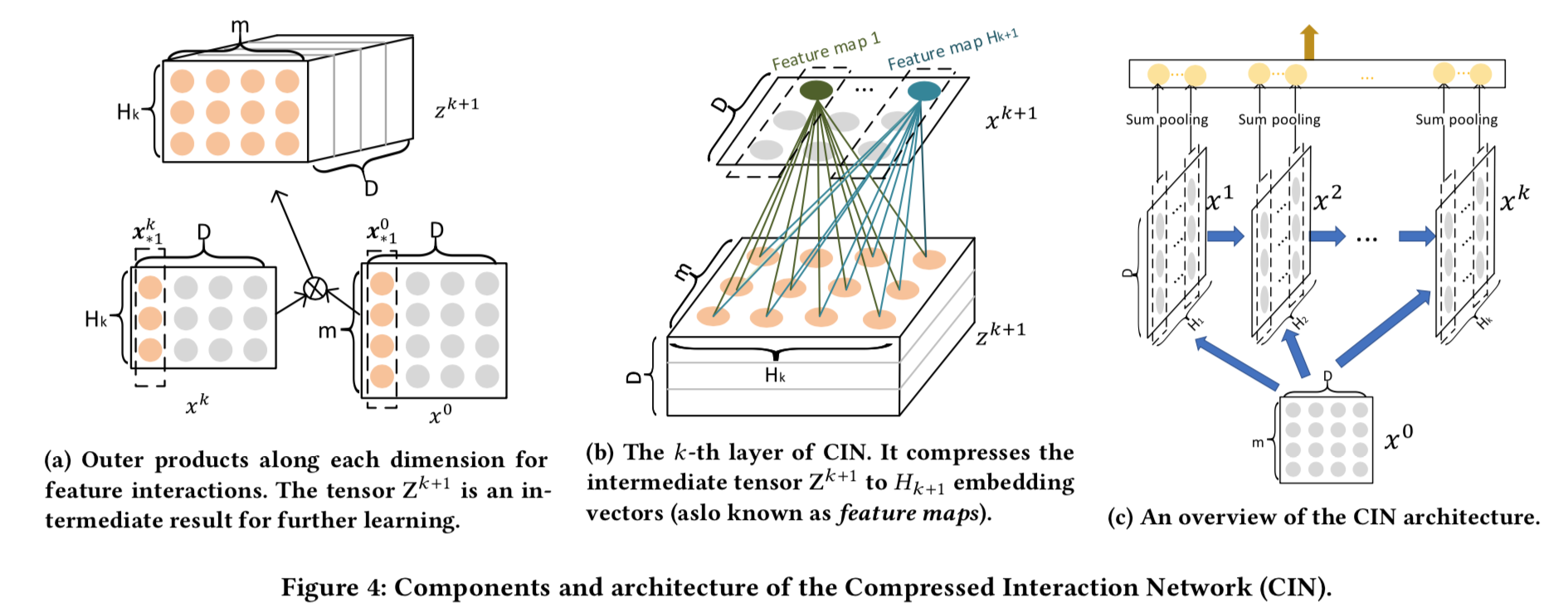
作者提出的 Compressed Interaction Network(CIN) 实现向量级别的交叉, 模型复杂度跟交叉次数指数增长(这个怎么验证)
CIN每一层都是Hk个D维向量,D保持不变,Hk可以变。生成方式是,将他们看做D个Hk维向量,和D个m维向量,然后依次将上一层的每一个向量和第0层(最原始的向量X0)的每一个向量做张量积,升维到 $(K = H_{k-1} \times m)$维向量,然后用一个 $(H_k \times K)$的矩阵投影到 $(H_k)$维。就得到了 $(H_k \times D)$维矩阵。这个操作实质上是在D方向上的每一维上做了一个双线性变换,让他们互相交叉。
如果双线性变换是张量积+sum Pooling,那么就是FM的操作了
最后在D方向上做了一个sum Pooling操作得到一个向量,每一层都有这样一个向量,这这些向量都拼接起来,形成一个特征向量,再送入逻辑回归

xDeepFM