理解利率
现值(present value)
现值(折现值) 是为了未来的现金流量折算成当前的现金价值,从而可以进行比较。
第n期到期的现金流CF折现的现值PV为
$$
PV = \frac{CF}{(1+i)^n}
$$
i是利率/收益率等。
直观解释: n年后给你CF元, 市场利率为i,那么这笔钱的在现在的价值就是现值PV。
四种信用市场工具
- 普通贷款, 到期偿还本息: 普通一次性贷款
- 固定支付贷款, 定期偿付部分本金和利息: 例如房贷, 分期贷
- 息票债券, 每期偿还利息, 到期偿还票债券面值的债券: 国债
- 贴现发行的债券, 没有利息, 到期偿还票债券面值的债券。所以一般要以低于票面价格卖出, 一般的公司债券都是这样
到期收益率
将债务工具未来所有的现金流CF按照收益率 i 折算的现值如果等于价格,那么i就是到期收益率。
- 一次性借款N元,一年后偿付本息, 假设利息为i, 那么收益率就是i
- 如果分两年, 方案一,每年都按照利率i偿还利息,到期后偿还本金; 方案二,到期后一次性安年利率i还本付息, 这两种收益率还是i吗? 显然第一年的利息如果存银行或搞理财, 第二年还可以获得额外的收益, 但是第二年的利息并没有这个优势,这说明虽然每年的利率是一样的, 但是第一种方案收益率应该高一些, 这正是因为现金的时间价值不一样。在这个例子中, 假设每年的收益率为r(与利率i区分), 对于方案一,第一年的利息现值为 $( i N / (1+r) )$, 第二年的利息现值为 $( i N / (1+r)^2 )$,确实不一样, 第二年的本金的现值为 $( N/(1+r)^2 )$, 根据等式,未来全部的现金流的现值等于价格(也就是本金), 那么有
$$
N = \frac{i N }{(1+r)} + \frac{i N} {(1+r)^2} + \frac{N}{(1+r)^2}
$$
所以到期收益率满足
$$
1 = \frac{i} { 1+r } + \frac{1+i}{(1+r)^2 }
$$
可以通过解这个方程解出到期收益率 $(r = i)$, 也就是说 到期收益率是把债务等效于按照每年付息, 到期偿还本金,这种还款方式的利率!!再来看第二种方案, 很容易列出方程
$$
N = \frac{2i N} {(1+r)^2} + \frac{N}{(1+r)^2}
$$
解出
$$
r = \sqrt{1 + 2i} - 1 \approx i - i^2 < i
$$
实际收益率是比年利率i小的。
- 等额本息, 到期收益率案例。以房贷为例, 100万元本金LV借款, 假设月利率为i, 按照每月等额本息方式还款n年, 每月还钱金额FP计算。
$$
LV = \frac{FP}{1+i} + \frac{FP}{(1+i)^2} + \frac{FP}{(1+i)^3} + ... + \frac{FP}{(1+i)^{12n}}
$$
所以
$$
FP = LV / (\frac{1}{1+i} + \frac{1}{(1+i)^2} + \frac{1}{(1+i)^3} + ... + \frac{1}{(1+i)^{12n}})
$$
以LV=1000000元为例,年利率为4.9%,那么月利率i=0.40833%,那么可以就算出 FP=5307元
def calc_fp(lv, i, n): r = sum(1/pow(1 + i, k) for k in range(1, n+1)) return lv / r if __name__ == '__main__': print calc_fp(726000, 0.0325/12, 12*30) # 实际值 3159.60 print calc_fp(940000, 0.0539/12, 12*30) # 实际值 5272.48
假设以等额本金方式还款, 那么每月还款金额很好算, 就是等额本金+当月的剩余借款产生的利息。
房贷计算参考loan_calc.py。
- 息票债券, 用P表示息票现期价格, C表示每期支付利息, F为债券面值,也就是到期后支付的金额,那么有
$$
P = \frac{C}{1+i} + \frac{C}{(1+i)^2} + \frac{C}{(1+i)^3} + ... + \frac{C}{(1+i)^{n}} + \frac{F}{(1+i)^{n}}
$$
C与F的比值也是息票利率, 如果息票现期价格P等于面值F,那么息票相当于每期还息到期还本的借款, 到期收益率就是票面利率。实际中,价格P往往和面值F不相等,如果价格P低于面值,那么到期收益率显然高于票面利率。这说明, 息票价格P与到期收益率负相关!!
- 永续债券, 就是指n等于无穷的息票债券, 类似于固定股息的股票。有
$$
P = \frac{C}{i}
$$
可以看到, 价格跟利率成反比!! 这也相当于一个简单的股票价格模型, 当市场无风险利率升高了, 股东要求的到期收益率也会相应提高, 也就是i会提高(这种情况下容易验证到期收益率就等于票面利率,你可以认为F=P,实际上在n无限大时,只要F为有限值,都没有影响), 那么股票价格就会下跌, 这样才能让当下的买家获得相应的收益率,这样交易才能完成!
- 当利率下降到很低的时候, 国库券/银行利率可能出现负利率!!因为大额的资金持有现金不方便。
回报率
- 对任何证券来说, 回报率(R)既包含了利率(ic)也包括价格变动率g(也叫资本利得率)!
$$
R = i_c + g
$$
不分红的股票就只有资本利得率g, 价格不变的债券就只有利率。由于价格波动可能为负的,这会导致回报率为负值!! - 利率风险: 债券期限越长,价格变动幅度受利率影响会越大,这会加大长期债券的投资风险! 股票可以认为就是一种无限期的债券!
- 距离到期日期限 和 持有期限 相同的债券是没有利率风险的。因为它的回报只有利息,到期时的价格就是约定的票面价格,也就是当初买的价格!
名义利率与实际利率
实际利率是指从名义利率(票面利率)扣除通货膨胀之后的利率。费雪方程(Fisher Equation)
$$
i (\text{名义利率}) = i_r (\text{实际利率}) + \pi^e (通货膨胀)
$$
据此,我们来测算一下2008年-2018年10年期间, 5年期定期存款的实际利率, 2008年时3年以上定期存款的基准利率为4.14%, 10年间年均通货膨胀率估计值约为7%(用M2增长率 - GDP增长率),这表明我们的名义利率为 -2.86%!!! 这跟我们直观感受一致, 「把钱存银行, 越存越没钱!」
| 时间 | M2同比 | 国内生产总值-同比 | 通货膨胀率 |
|---|---|---|---|
| 2017年 | 8.20% | 6.90% | 1.30% |
| 2016年 | 11.30% | 6.70% | 4.60% |
| 2015年 | 13.30% | 6.90% | 6.40% |
| 2014年 | 12.20% | 7.30% | 4.90% |
| 2013年 | 13.60% | 7.80% | 5.80% |
| 2012年 | 13.80% | 7.90% | 5.90% |
| 2011年 | 13.60% | 9.50% | 4.10% |
| 2010年 | 19.70% | 10.60% | 9.10% |
| 2009年 | 27.68% | 9.40% | 18.28% |
| 2008年 | 17.82% | 9.70% | 8.12% |
| 平均 | 15.12% | 8.27% | 6.85% |
数据来源: http://data.stats.gov.cn/easyquery.htm?cn=C01
注意事项: GDP同比增速是指GDP平减指数, 如果你根据GDP实际值算会高不少, 要用国家公布的GDP增长数据, 那个数据是已经扣除了物价之后的。
参考 中国近10年的通货膨胀率大概在多少? - 江枫渔火的回答 - 知乎
问题: 为什么算通货膨胀也要用扣除物价指数之后的GDP增长率?
名义利率无法直接观测到,1997年,美国财政部发行了指数化债券TIPS(全称通货膨胀保值债券),债券的利率按照物价水平变化进行调整。
利率行为
- 由于债券价格跟利率存在负相关, 所以可以通过债券市场和货币市场的供求分析来研究利率变动机制。所以关键是导出资产的需求曲线和影响资产需求的因素。在本章中, 只考虑一种证券和一种利率, 在下一章中会考虑多种利率之间的关系, 也即是利率的期限结构。
- 资产需求的决定因素:
- 财富
- 财富增加会让我们拥有更多资源购买更多的资产, 所以财富的增长会带来资产需求量的上升
- 预期收益率
- 显然在其他因素不变的情况下, 本资产预期收益率的上升会导致资产需求的上升
- 而其他可替代资产的预期收益率的上升会导致对本资产的需求的下降
- 风险
- 风险越大,对该资产的需求就会越低
- 流动性
- 资产变现的速度叫流动性, 其他因素相同的情况下, 流动性越高, 需求越高
- 财富
- 资产需求变动
- 财富的变动
- 在经济周期的扩张阶段,经济迅速增长,财富会不断增加,从而导致对债券的需求上升。
- 预期收益率的变动
- 如果预期收益率会提高, 会降低对当前债券的需求。注意区分预期收益率「高」和「将会变高」,一个说的是值,一个说得是变化,因为未来会变高,说明当前的收益率是偏低了,所以会降低当前对债券的需求。预期收益率的变化影响的是长期债券的的需求,而短期债券(一年内的)不受影响,因为预期收益率的变化对它们的收益率没有影响,对长期债券来说,预期收益率的提高会降低未来长期债券的价格,所以会影响它的资本利得。
- 风险变动
- 如果债券市场的价格波动幅度加大,那么债券投资的风险水平就会提高,因此对债券的需求就会降低
- 相反,如果股票市场等其他资产的风险增加,那么债券的风向相当于降低,会增加对债券的需求
- 流动性变动
- 流动性增加会增加对债券的需求
- 其他资产的流动性增加会降低对债券的需求
- 1975年,美国废除了股票佣金规则,大幅降低了股票交易过程中得劲交易费用,相当于增加了股票的流动性,导致了债券需求的降低
- 财富的变动
- 债券供给的变动
- 投资的预期盈利能力
- 在经济扩张周期中,经济高速增长,投资的预期盈利能力也会相应提高,会增加债券的供给
- 预期通货膨胀率
- 预期通货膨胀率提高,利率却没变,那么真实的借款成本会下降,会增加债券的供给
- 费雪效应: 预期通货膨胀率的变化影响名义利率。预期通货膨胀率的提高,增加了借款成本,从而增加了债券的供给, 在需求不变的情况下, 导致了债券的均衡利率上升。 因为只有给更多的利率,才能增加需求量,债券才发的出去。
- 经济扩张和收入提高会导致利率的上升?
- 日本低利率的解释: 90年代末21世纪初, 日本出现了极低利率,在1998年11月,出现了负利率。这是因为经济衰退, 出现了通货紧缩和负利率。通货紧缩会增加对债券的需求,因为投资收益降低,债券收益稳定,这导致债券需求的增加; 另一方面, 通货紧缩增加了实际利率,导致债券的供给降低。需求增加,供给降低,从而导致债券价格的提升,利率的降低。
- 过低的利率甚至负利率是经济出现严重问题的标志,并不是好事。
- 政府预算
- 财政赤字导致政府债券的供给增加
- 投资的预期盈利能力
- 凯恩斯流动性偏好理论
- 人们利用储藏财富的资产主要包括货币和债券。经济运行的过程中,财富总量等于二者之和。一种资产的需求量降低,必然提高另一种资产的需求量。货币不包括不支付利息的现金。
- 利率上升会增加货币的需求,导致债券需求降低,债券价格就会降低。
- 货币需求的变化
- 收入效应: 经济扩张和收入增加,人们愿意持有更多的货币
- ????
- 物价水平效应: 物价水平上涨,会导致人们持有更多的货币
- 收入效应: 经济扩张和收入增加,人们愿意持有更多的货币
- 货币供给的变动
- 央行货币供应量的提高将增加货币供给
- 收入水平的变动:经济扩张周期,收入水平提高, 相同利率下, 作为价值储藏的货币需求也会提高,从而导致利率上升?
- 物价水平的变动:物价水平提高导致相同利率下的货币需求的提高,从而利率上升
- 货币供应量的提高将会导致货币供应的提高,从而利率下降
- 货币与利率的负相关? 诺贝尔经济学奖得住弗里德曼提出了重要的批判, 货币供应量的提高,会降低利率,这确实没错,他将这种效应叫做流动性效应。然而,他认为流动性效应只反映了货币和利率关系的一部分,货币供应量的提高还会改变其他变量,具有额外的效应。
- 收入效应: 货币供应量的提高会对经济产生扩展的影响, 从而增加收入和财富水平, 这会导致利率的上升
- 物价效应: 货币供应量的提高会导致物价水平的上升, 从而增加相同利率下的货币的需求, 提高利率, 物价效应并不会马上生效
- 预期通货膨胀效应: 货币供应的提高会导致预期通货膨胀率的上升, 从而提高名义利率。 预期通货膨胀效应会马上生效
- 实际情况是, 流动性效应很弱, 物价效应和通货膨胀效应占主导
- 我国币供应量与期国债3月收益率曲线如下图, 可以看到09年大放水,导致利率的大幅降低,从3.5降低到1。(M2看左轴,收益率看右轴)
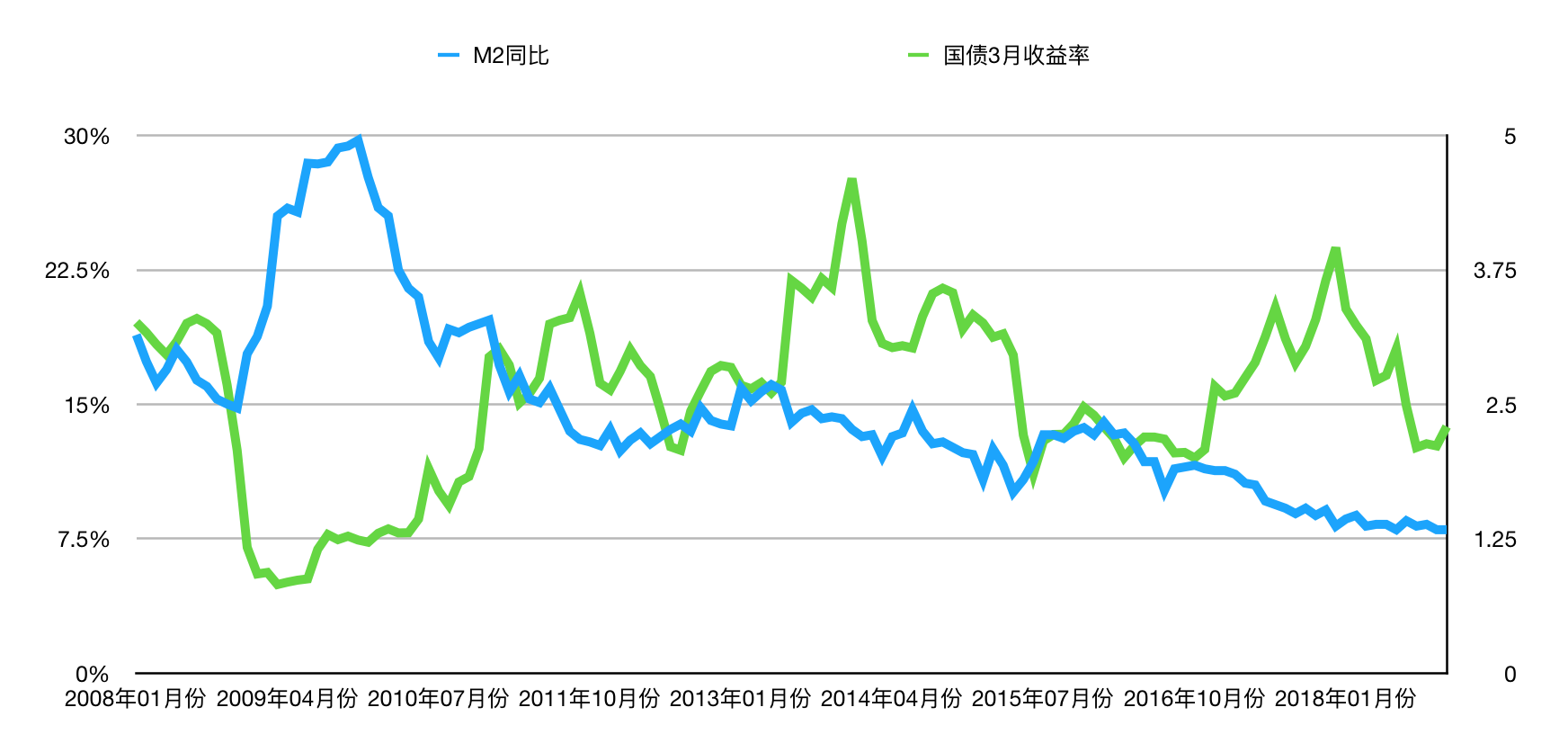
利率的风险和期限结构
风险和期限结构
- 利率的风险结构: 违约风险, 流动性, 所得税
- 相同期限, 风险越高的债券,利率越高,额外的利差也叫风险溢价 risk premium
- 信用评级机构提供债券的评级, 在美国,低于Baaa级别的债券也叫垃圾债券,利率高
- 流动性: 交易量越多的债券流动性越好, 国债的交易量最多,流动性最好。
- 公司债券和国债的利差不仅仅反映风险,还反映了流动性。所以风险溢价更确切的是「风险和流动性溢价」
- 所得税因素,美国投资市政债券获得的利息收入可以免交联邦所得税
三种理论
-
利率的期限结构
- 将那些具有相同风险、流动性和税收特性而期限不同的债券收益率连成一条曲线,成为收益率曲线(如下图所示的2019-01-04日的国债收益率曲线)
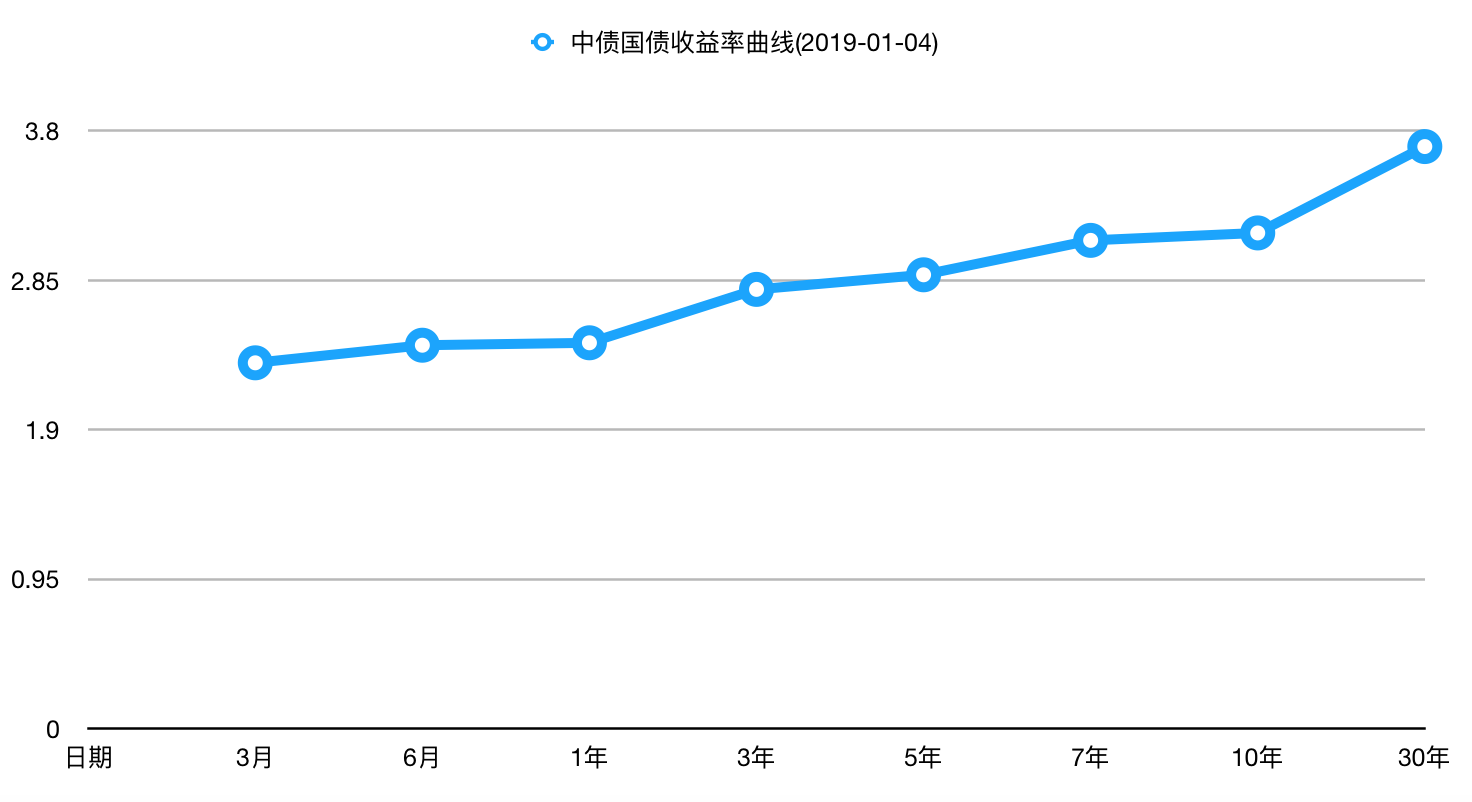
- 如果短期利率较低,收益率曲线通常向上倾斜;如果短期利率较高,那么收益率曲线更多是向下倾斜,即反转的收益率曲线。
- 反转的收益率曲线比较少见,可以从不同期限的债券利率随时间变化图中看到,短期债券利率高于长期债券利率只有少数的几天。
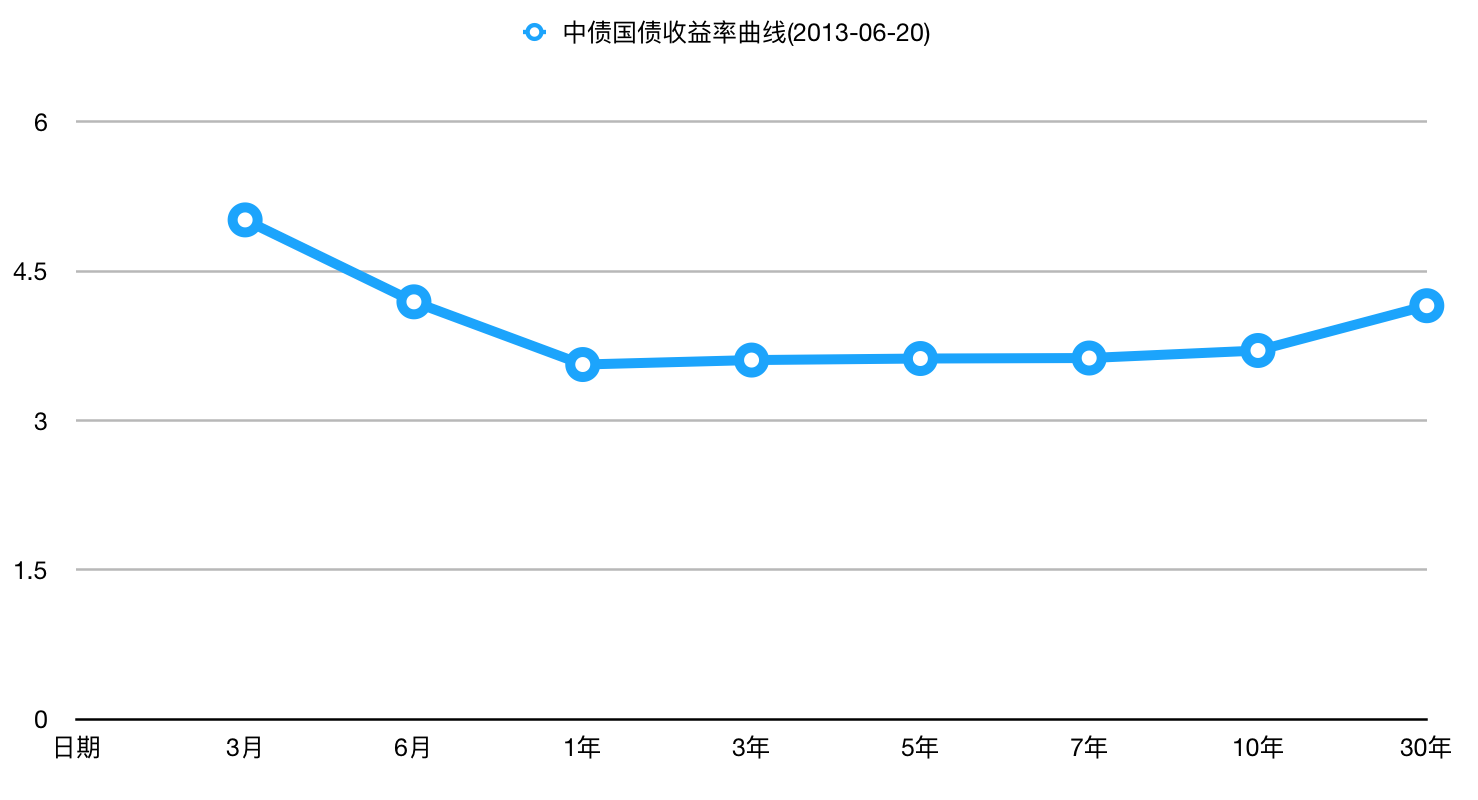
- 不同债券的利率会随着时间的推进,出现相同的变动趋势(见下图)。
- 将那些具有相同风险、流动性和税收特性而期限不同的债券收益率连成一条曲线,成为收益率曲线(如下图所示的2019-01-04日的国债收益率曲线)
-
预期理论,市场分割理论,流动性溢价理论是用来解释上述期限结构的三重理论。
- 预期理论基本假设: 长期债券的利率等于在长期债券到期期限内短期利率的平均预期值。
- 所以,如果短期利率过低,那么短期利率很有可能低于未来一段时间的短期利率平均值, 所以短期债券利率低于长期债券利率
- 默认假设,债券购买者对不同期限的债券没有任何偏好差异, 相当于不同期限的债券可以完全替代, 这与实际不符。
- 假设未来5年内该债券的利率期望值为 5%,6%,7%,8%,9%, 那么5年期的该债券利率为平均值 7%。
- 这个理论的一个推论是,只有在短期利率的预期值上升的条件下,现期的长期利率才会高于短期利率,而实际上,长期利率几乎总是高于短期利率
- 市场分割理论: 认为市场上不同期限的债券之间完全不可替代,相当于另外一个极端
- 由于通常情况下,长期债券的需求量较小,其价格较低而利率较高,所以收益率曲线通常是向上倾斜的。它解释了预期理论无法解释的这个问题
- 但是无法解释短期利率和长期利率具有相同的变动趋势
- 无法解释短期利率的变动对长期债券供求关系所产生的影响, 也就是在短期利率很高的时候,收益率曲线会出现反转
- 流动性溢价理论: 结合预期理论和市场分割理论, 长期债券的利率等于长期债券到期期限内的短期利率平均值加上随着该债券供求状态变动而改变的流动性溢价(也较期限溢价)。
- 它假设不同期限的债券可以互相替代(跟预期理论相同), 因此短期利率的变动会影响长期利率。但是该理论允许投资者对不同期限的债券存在偏好,比如更偏向于短期债券,也就是流动性高的债券,而长期债券的低流动性需要一个流动性溢价,牺牲流动性的补偿。
- 因为流动性溢价的存在,导致长期债券通常都是高于短期债券的
- 如果短期债券利率突然特别高, 比如在2013年06月底、2013年年底和2017年底有少数几天,短期利率突然暴涨,长期债券即使有流动性溢价,也没能超过短期利率。
- 利率期限结构的实证研究
- 由于收益率曲线包含了未来利率的预期值的信息, 所以可以使用收益率曲线来预测通货膨胀率和经济周期的未来情况
- 经济繁荣时期,利率随之上升,而在经济衰退时期,利率随机下降。平坦或者向下倾斜的收益率曲线意味着未来短期利率预期值将会下降,经济往往处于衰退阶段
- 陡峭的收益率曲线意味着货币政策处于宽松状态,而平摊或者向下的收益率曲线意味着货币政策处于紧缩状态。
- 下图计算了1年期以内的短期国债利率平均值与1年期以上的长期国债利率平均值之间的差值, 不妨把这个差值叫做期限溢价(图中的利率先按月平均了)
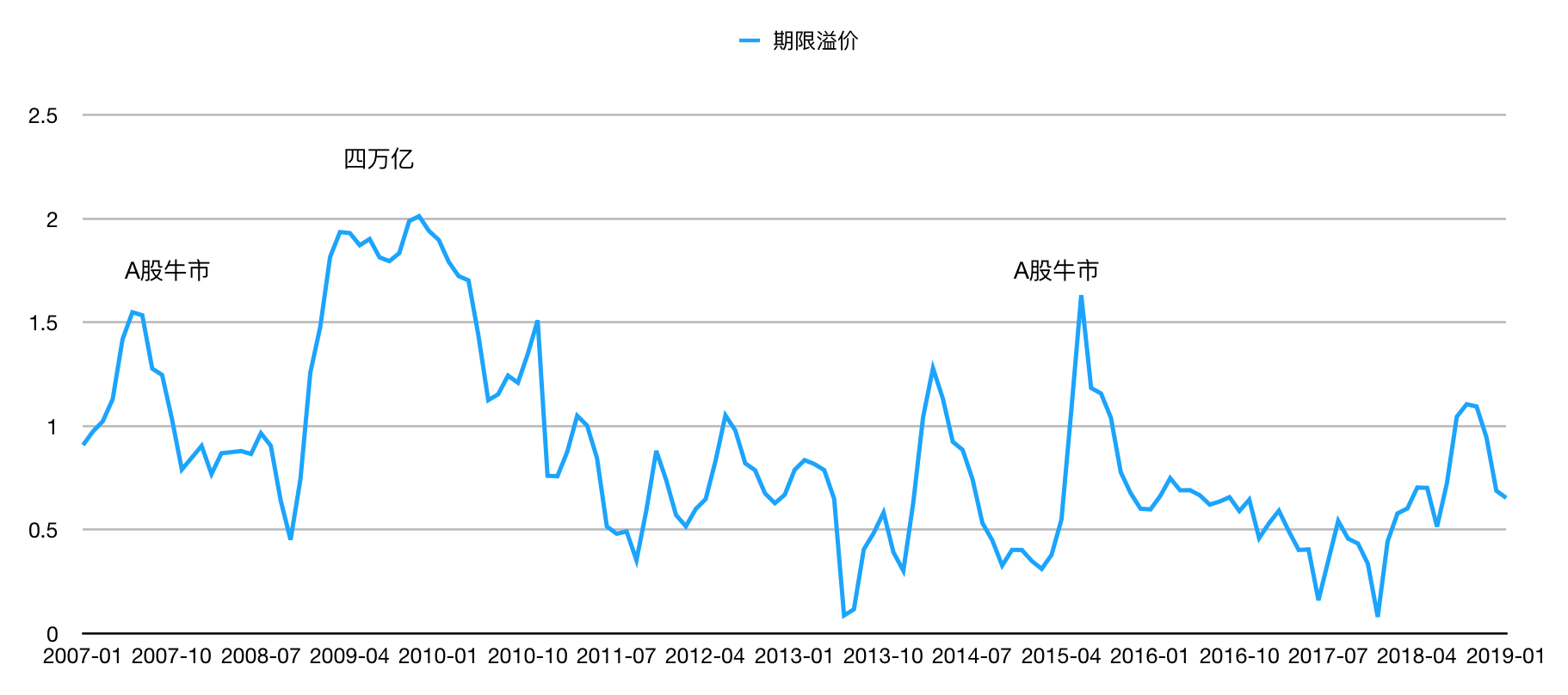
- 可以看到2009年,溢价达到2个点,正是四万亿大放水的货币宽松; 类似的还有2015年年中和2007年年中,分别对应A股的两次大牛市; 而在2017年期间,溢价处于很低的值, 正是收紧信贷降杆杆的期间。
- 大放水的时候, 短期收益率会很低,长期收益率一般变化比较缓慢,所以产生了很大的期限溢价; 而在牛市期间,国债的收益过低,大家都拿钱炒股,所以收益率曲线就会很平,甚至如果短期流动性较低时出现反转,此时的期限溢价就很低。可以参考 基础知识讲堂:收益率曲线,如何用它预测经济大势?
- 但是收益率曲线貌似是政策和市场行为的结果反映,用来预测是不是不太现实,预测牛市逃顶?哈哈
股票市场、理性预期理论和有效市场假说
股票市场
- 普通股股票价格的计算
- 股票的两个重要权利: 投票权 和 对流入公司全部资金的剩余求偿权。
- 任何投资的价值都可以通过计算该项投资在其生命周期内产生的全部现金流的现值来衡量
- 单期估值模型:
$$
P_0 = \frac{Div_1}{1 + k_e} + \frac{P_1}{1 + k_e}
$$
其中P0是当期的估值,P1是预期到期后的价格, Div1 是该期的分红, ke是要求的收益率。如果当期股价不高于你的估值P0,那么股票就有买入价值。 - n期估值模型
$$
P_0 = \frac{D_1}{1 + k_e} + \frac{D_2}{(1 + k_e)^2} + ... +\frac{D_n}{(1 + k_e)^n} + \frac{P_1}{(1 + k_e)^n}
$$
如果n很大的时候,最后一项趋近于0,可以忽略, 那么
$$
P_0 = \sum_{i=1}^{\infty}\frac{D_i}{(1 + k_e)^i}
$$
因为在这个无穷级数中, Di 未知难以直接求和,所以有一些根据对Di的一些假设的计算模型 - 戈登增长模型(Gordon growth Model): 假设红利具有固定不变的增长率
- 红利增长率一直很定不变
- 红利增长率必须低于要求收益率ke
- $( D_i = D_0(1+g)^i )$, g是红利增长率
- $( P_0 = \frac{D_1}{k_e - g})$
- 市场中股票价格的确定
- 价格是由愿意出具最高价格的购买者来确定的
- 价格是由该资产使用效率最高的购买者来确定的, 因为使用效率高的人对资产的定价会更高
- 信息在资产定价中发挥重要的作用, 如果你有一些别人不知道的信息, 那么你更有可能出更合理的价格。对于不了解公司的人来说,对公司的风险具有更不确定性,所以他们要求的收益率ke会比较高。相反,如果你知道公司的一些运营信息,你要求的收益率ke会比较低,所以你的出价会更高。
- 新的信息会导致对该股票的红利水平和风险水平被重新评估, 股价也被重新评估
- 货币政策对股价的影响
- 央行利率的降低,导致投资人对ke要求降低, 股价自然会涨; 相反加息会降低股价
- 次贷危机增加了股票的风险,导致投资人对ke要求提高, 股价也因而降低
理性预期理论
- 适应性预期认为某个指标(比如通货膨胀率)的预期值被认为是过去该指标的平均值, 这种方法被上个世纪五六十年代的经济学家使用,但后来被认为是错的。
- 约翰·穆斯发展出理性预期理论, 该理论认为: 预期结果将会等于使用全部信息获得的最优的预测结果,不仅仅是历史的信息
- 理性预期的解释: 实际上就是我们所说的模型的上限。
- 如果存在一个十分重要的额外因素,但是无法活动相关信息,那么没有考虑这一因素的预期结果依然是理性的。比如所有人都不知道下个月央行加息,那么现有的价格预期仍然是理性预期。因为这个事情在当下,任何人都不知道。
- 理性预期理论的理论基础, 为什么人们会使用他们知道的所有信息预测得到最好的结果, 因为如果不这么做,就会付出很高的代价。比如遭受经济损失!因而,在金融市场中,用全部信息预测最优预测结果动机十分强烈,其结果是「有效市场假说」。
有效市场假说
- 其实只是理性预期理论在金融市场中证券定价问题中的应用结果而已
- 前提: 金融市场汇总的证券价格能够完全反应全部可用信息这一迁移假设基础之上
- 理论基础
- 套利: 指市场参与者消除未使用的盈利机会(信息)的过程。
- 纯套利: 盈利机会不包含风险
- 普通逃离: 存在一定风险
- 有效市场假说也可以表达为: 在有效市场中, 所有未利用的盈利机会都会被消除
- 套利: 指市场参与者消除未使用的盈利机会(信息)的过程。
- 强势版本: 在有效市场中,所有的价格都是正确的,并且反应了市场基本面(即能够对证券未来收益数额产生直接影响的要素)。
- 有效市场假说对投资的应用:
- 《旧金山纪事报》将猿猴选的股票和股票专家选的股票对比他们的绩效表现,发现难分胜负。
- 如果专家公布了是有短缺将不断加剧, 你应该用全部积蓄来投资石油股票吗?
- 根据有效市场假说,我们不能期望超过正常水平的高收益率,已经公布的信息的结果已经反映在当前股价中了,所以我们无法获得额外的收益。
- 绝大多数市政经验表明, 投资分析专家提供的建议不能保证我们获得超过市场正常水平的投资绩效。(在有效市场中, A股要除外吧, 各种内幕)
- 一个幻想致富的人发明一种高明的骗术,每周都会写两份信, 在信A中,他预测A对能在足球比赛中获胜, 在信B中,他预测B对能获胜。然后他把用户的地址分为两组,一组发信件A,一组发信件B。在下一周中,他只会对上周预测正确中的用户中,重复上述步骤。在进行10场比赛之后,就会有一部分10场都预测正确的人。随后他向这些人发最后一封信,声称他是足球预测转件,除非他们支付大笔费用,他才会继续提供预测结果。这说明,即使我们无法精确预测市场结果,市场中依然会有一些持续成功的人。
- 你应该信一些小道消息吗? 有效市场假说告诉我们,小道消息也已经反映在价格中了。除非你是最早得知这一消息的人,你才能获得超过正常水平的高额收益。
- 好消息总能促使股价上涨吗? 当市场已经预期到这种好消息了,那么股价不会发生变化, 只有公布未知的信息才会导致股票价格发生变化。比如不及预期,或高于预期。和预期一致不会使股票发生任何变化
- 有效市场假说为投资者提供的建议,投资人(我们中的绝大多数人都属于此类)不应该视图通过频繁地买卖证券来获得超过市场正常水平的收益, 除了能够增加交易佣金外没有任何意义!
- 对小型投资者而言,他们相对于投资规模的投资组合管理成本较高,所以购买某种共同基金投资工具而不是购买单只股票是一种合理的策略。并且,有效市场假说告诉我们,没有任何基金能够长久地获得超过市场正常水平的收益,所以应该买低佣金费用的共同基金产品。
- 经济基本面之外的某些因素也可能对股价产生影响
- 行为金融:
- 如果股票价格上涨到非理性水平时,要将他们拉回基本面的水平,需要有做空机制
- 实际上人们很少做空, 损失厌恶
FAQ
折现公式中的折现率如何确定
- 折现率取决于应用场景,比如在计算只进行无风险投资的情况下,未来的钱的现值,那么折现率就是无风险利率。
- 而对于计算股价是否合理时,则变成期望的收益率;
- 在计算住房贷款每期付款时,则变成贷款利率。
注:现值的计算是一种比较主观的东西,不是一个客观的数据。
债券基金为什么有负的收益,为什么会有高于票面利率的收益
- 因为存在利率风险和违约风险,导致负收益。