机器学习漫谈
前不久,国务院发布了《新一代人工智能发展规划》[1],将人工智能上升到国家战略高度,中国希望借助人工智能重回世界科技的中心; 紧接着科技部又发布了人工智能发展规划[2],并依托四大单位:百度、阿里、腾讯、科大讯飞,建立新一代人工智能创新平台! 如果要问现在什么是风口行业,毫无疑问是人工智能!机器学习是当前实现人工智能的一种途径,也是目前的最佳途径! 在这篇文章中,将自己的机器学习的些许感悟,总结起来,希望着眼当下,展望未来。
机器学习之道
机器学习的本质——归纳法
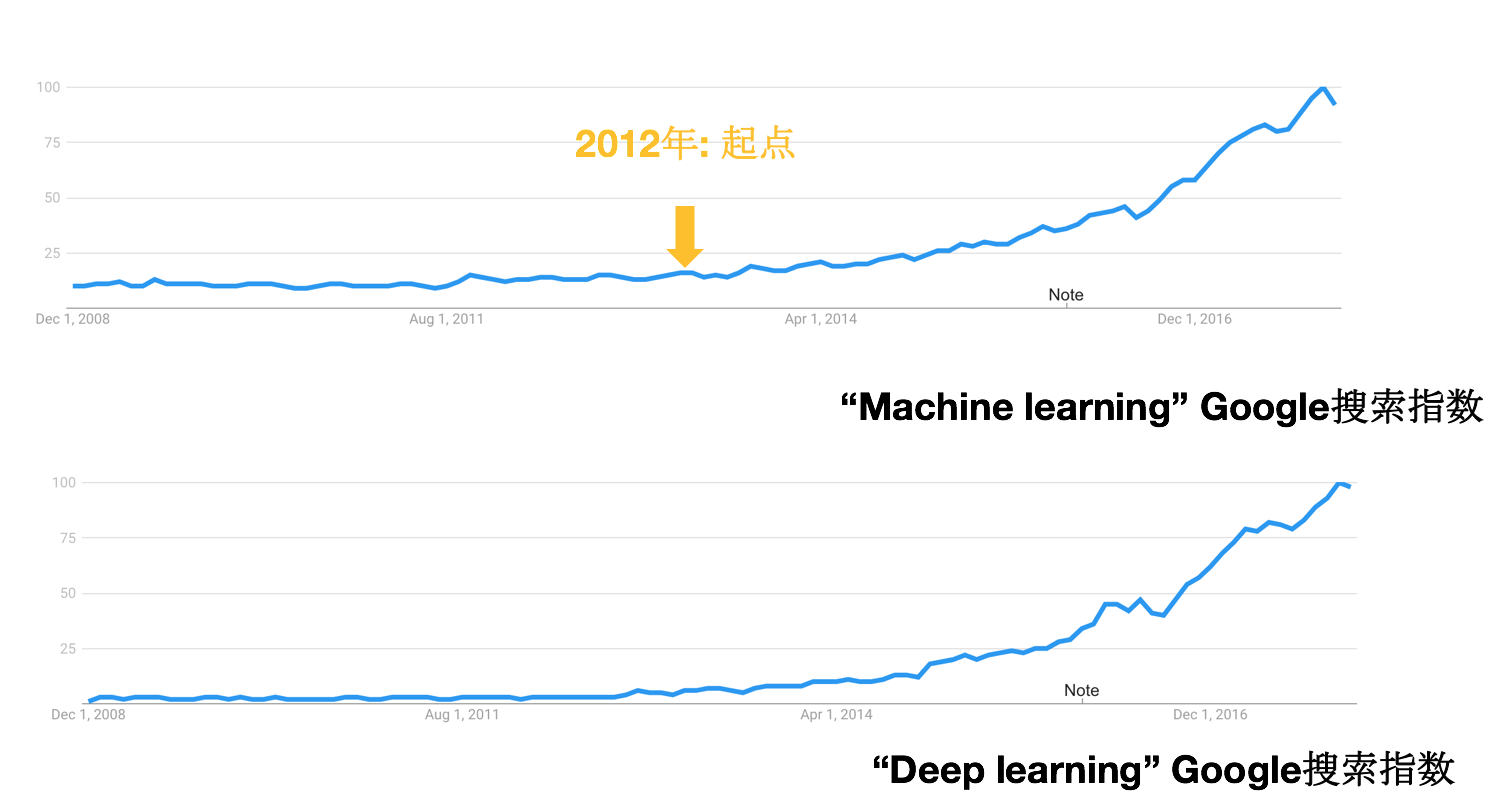
说到机器学习,几乎都会与另外一个词“人工智能”挂钩,现在人工智能的火爆程度丝毫不亚于2002年左右的互联网的火爆。 还有一个词也是业界津津乐道的,那就是“深度学习”。 如果你上google搜索 machine learning 和 deep learning,你会发现这两个词的搜索指数非常相似! 事实上,机器学习这个领域已经发展很多年了,这一波机器学习的火爆正是伴随着深度学习而爆发的,尤其是在2012年的两个里程碑式的工作:
- Hinton和学生Alex利用一个深层的卷积网络把ImageNet比赛刷到的新的记录,拿到当年的冠军[3]。
- Hinton和微软的研究者将DNN用于语音识别的声学模型,为10年未有明显突破的语音识别技术带来了新的曙光[4]!
虽然这一波机器学习的火爆是由于深度学习的突破,但是很多学者表示,深度学习并非什么新的技术,所用的神经网络DNN、CNN、RNN都是之前就提出过的,更多的改进是由于算力、数据量的提升,当然并不是说模型没有突破,模型上也有很多改进,但都谈不上突破式的创新。 事实上,这种说法基本是正确的,直到生成对抗网络GAN的提出,LeCun把GAN称作“过去十年机器学习界最有趣的idea”。 但是,不论如何,深度学习带来的飞跃确实是看得见的!看看现在无论是初创公司还是传统公司,言必称自己是人工智能公司就知道有多么大影响力了!
不论是这一波火爆的深度学习,还是经典的机器学习算法,他们的本质并没有什么区别,都是 利用某种算法从数据中自动归纳出有意义的规律的一种方法。
我们知道,人类的推理方法大致可以分为两种,一种是演绎法,另一种是归纳法。
所谓演绎推理(Deductive Reasoning),就是从一般性的前提出发,通过推导即“演绎”,得出具体陈述或个别结论的过程。演绎推理的逻辑形式对于理性的重要意义在于,它对人的思维保持严密性、一贯性有着不可替代的校正作用。我们熟知的很多数学证明方法,例如通过简单的几条公理,推导出整个欧式几何大厦的推理过程,就是典型的演绎推理。 下面是演绎推理里面一个典型的三段论推理的例子:
- 知识分子都是应该受到尊重的,
- 人民教师都是知识分子
- 所以,人民教师都是应该受到尊重的。
演绎推理的核心思想就是从一般到特殊,将一些已经为真的通用性结论应用到具体的问题当中,得到具体的情况下的结论。这种推理方式保证了推理的严密性!在上述例子中,前两条就是一般性结论,知识分子是比人民教师更大的概念,第三条的结论就是将第一条结论应用到人民教师这个具体的个体上得到的更具体的结论!
有趣的是,柯南道尔的著名小说中《福尔摩斯》中的大侦探福尔摩斯也十分推崇“演绎法”!为此,老美还专门拍了一部剧《福尔摩斯:基本演绎法》! 只不过,福尔摩斯所声称的一般性结论和推理方式非常人能理解!

事实上,在早期的人工智能中,采用的也正是这种演绎推理。例如早期的专家系统,定理的机器证明,符号计算等等。 在专家系统中,知识被表达成很多条件命题,推理系统利用这些知识进行演绎推理得出结论!
而归纳法是根据一类事物的部分对象具有某种性质的有限观察,推出这类事物的所有对象都具有这种性质的推理,叫做归纳推理(简称归纳)。归纳是从特殊到一般的过程,它属于合情推理。通常归纳法难以保证结论是可靠的,例如,下面就是经典的归纳法的例子:
黑天鹅事件
17世纪之前,欧洲看到过的天鹅都是白色的,所以当时欧洲人归纳出一个结论:天鹅都是白色的! 直到后来,欧洲人发现了澳洲,看到了当地的黑天鹅,人们才认识到这个结论是错误的!
从有限的经验归纳出来的结论当然不见得是可靠的,但是数学上也有完全归纳法,可以保证结论是可靠的的例子,我们以前学过的数学归纳法,从命题\(P_n\)推到\(P_{n+1}\)就是一个例子!
从逻辑推理的角度来看,我们现在所用的机器学习就是先观察到一些数据,然后从这有限的数据中归纳出一些有用的规律的过程! 因此,机器学习本质上就是在做归纳推理,并且是不完全的归纳法!我们前面说到,这种不完全归纳法无法保证结论的正确性,所以如果机器学习模型预测错了,请不要怪他,因为它是在做不完全归纳,肯定会犯错的!但是这并不意味着就没有用,事实上我们人类很多经验都是通过不完全归纳法归纳出来的,甚至可以说几乎所有实际的经验都来源于不完全归纳,完全归纳法只有在数学上才存在。只要归纳的结论大多数情况下是对的,那么他就是有用的!
前面我们说了,机器学习本质就是从数据中自动归纳出有用的规律。那么,反过来,如果一个任务是从数据中去找规律,那么这件事就可以试试用机器学习来做,往往可以做得比人还好!下面是一些已经应用机器学习算法的例子
- xxR预估:CTR(点击率),CVR(转化率、下单率),司机接单率 etc。各种R的预估是应用机器学习的一个典型的场景,也是目前机器学习算法应用最多的场景之一!
- 视听说听读写:CV(机器视觉),ASR(自动语音识别),STT(语音合成),NLP(自然语言处理),MT(机器翻译),QA(问答)etc。这个场景也是目前人工智能吹得最火的场景,各种超越人类!
- 生物医学:基因工程、医学图像、诊断!比如,Google最近就声称利用机器学习算法对电子病历进行分析[5],未来机器学习在医学上的应用应该价值重大!
- 物理:希格斯玻色子挑战[6],利用算法找到区别于背景的有价值事件信号;量子多体波函数的建模[7] etc
- 化学:利用机器学习预测化学分子性质[8-10],研究人员通过理论仿真了很多分子的性质与参数关系,但是每次仿真都耗时巨大,于是想到了利用已有的仿真数据,建立一个机器学习模型来学习这个预测函数!
- 计算机科学:利用机器学习做数据库索引[11],Google科学家重新审视了数据库中的B+树索引,发现它就是一个回归树,因此想到用机器学习方法来建立索引。
纵观以上应用场景,可以发现都是有了很多数据,需要从数据中归纳出一些结论,因此这些问题可能就很适合应用机器学习来解决! 如果你也想在工作中应用机器学习,那么你得首先思考一下,你的工作内容是否可以看做从数据中找到一些规律的问题,如果答案是肯定的,那么就不要犹豫了,马上试试机器学习的方法,说不定就会有意外的收获!
监督学习的本质——函数拟合
机器学习的方法大致可分为两大类,监督学习和无监督学习,前者是目前应用最为广泛的方法。两者的区别在于观测的数据是否有标注! 简单来说,如果给你很多照片,要你用算法从这些数据中建立一个模型来找出人像和风景照,那么就是无监督的!如果这些照片已经是标注好的,也就是说每张照片都打上了一个标签,告诉你是人像还是风景照,那么这个问题就是监督学习!
通常监督学习比无监督学习更容易,因为有了监督信号告诉你对还是不对!监督学习本质上就是在函数拟合! 比如上面的例子,输入一张照片,要你输出这张照片是人像还是风景照!这就是一个数学函数
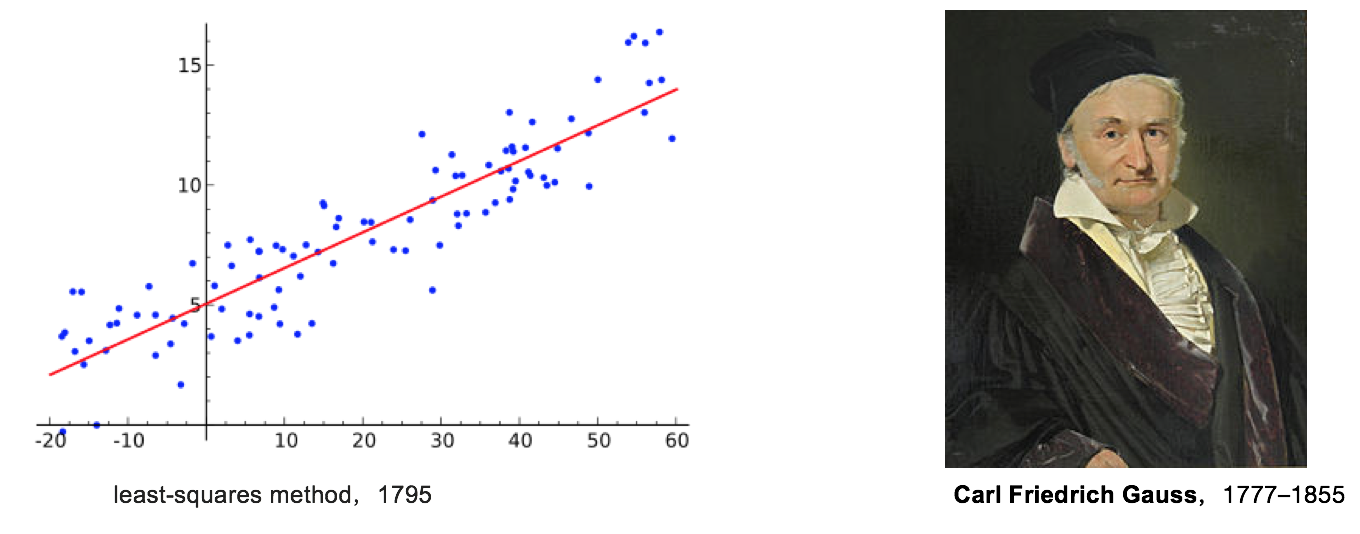
\[h(X) = \begin{cases} 1, \text{如果照片X是人像} \\ -1, \text{如果照片X是风景照} \end{cases}\]函数拟合这件事情,最早可以追溯到18世纪大数学家高斯的最小二乘法。早在18世纪,数学家高斯就开始研究怎么根据观察到的一堆数据,把拟合最好的直线找出来的问题。这个方法,在高中数学中就学习过,方法也很简单,就是找到一条直线\(\hat{y} = ax + b\)使得拟合误差\(\sum_i (y - \hat{y})^2\)最小!利用很简单的数学推导就可以得到最佳的参数!这个方法就是最小二乘法,可以应用到高维情况,并且最优参数有解析解!
高斯最小二乘法跟现在机器学习用的线性回归模型并没有什么太大区别,只是在损失函数上做了一些适应于特殊环境的改进。 监督学习另外一类问题就是前面的例子中提到的问题,分类问题。分类和回归的区别在于拟合的目标变量\(y\)的取值构成的是无限集合还是有限集合。如果是无限的,通常认为是回归问题,比如预测房价;如果是有限集合,通常认为是分类问题,比如预测股价涨和跌,照片是哪种类型等等。 分类问题要拟合的函数是不连续的,因此难以直接拟合。除了一些决策树算法可以直接拟合不连续的分类函数外,大多数算法都是通过拟合样本属于每一类的概率来间接拟合这个不连续的函数。一旦这个概率拟合好了,然后找出概率最大的作为输出就得到了最终的分类函数了!
\[\hat{y} = \arg\max_i P(y=i|X)\]线性分类模型对输入做线性加权打分后,然后用softmax归一化得到概率,最优的权重通过极大似然估计得到。
不论是简单的线性模型还是现在火热的深层模型(深度学习),本质上都是在拟合一个函数!
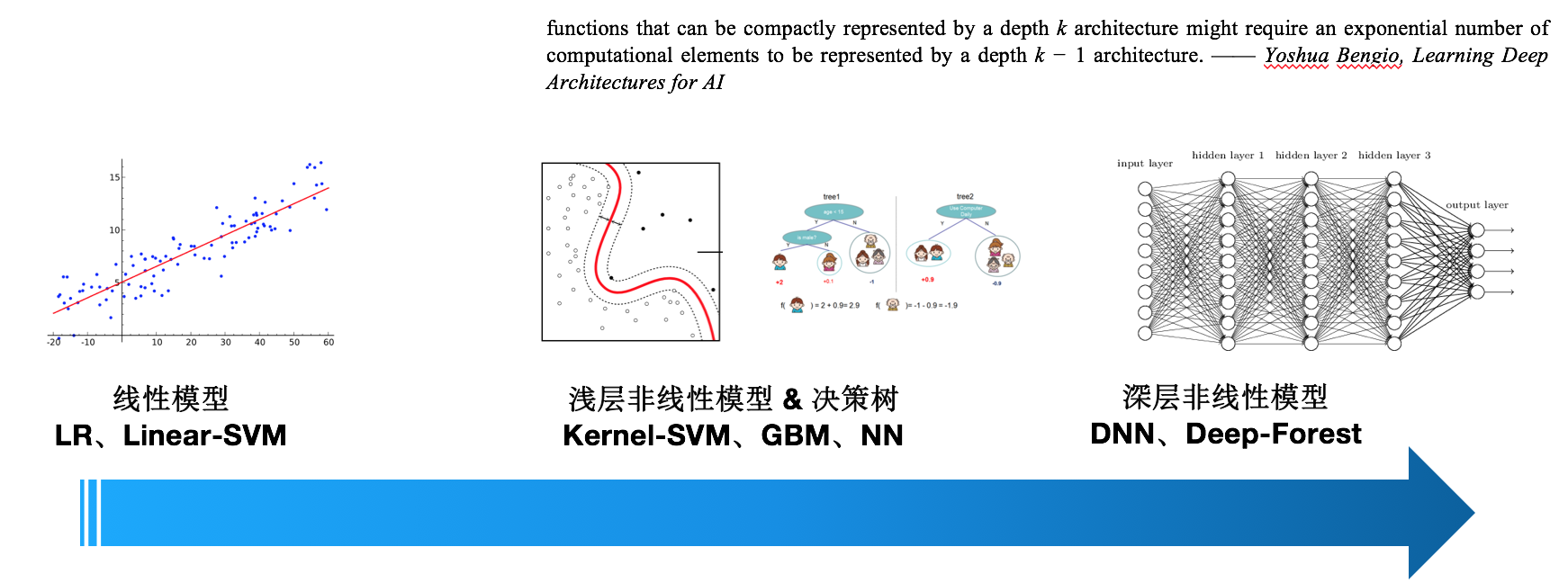
不同模型的拟合能力各不相同,比如线性模型,就只能拟合一个线性函数,而广义线性模型实际上也看做线性模型,只不过是在线性模型后面加个一个非线性函数,特征之间还是按照线性加权得到的,后面的非线性函数是为了适应响应变量。例如逻辑回归,虽然最后加了一个sigmoid函数,但是分类面(或等值面)还是超平面,所以一般把广义线性模型都看做线性模型!线性模型简单好解释,但是无法直接拟合特征与目标之间的非线性关系,以及特征间的非线性关系!通常需要很多特征工程,例如离散化,特征交叉组合等等。非线性模型就好一些,可以直接拟合这些非线性。而目前主流的深度学习的拟合能力最强,在相同的复杂度(参数)下,它比浅层非线性模型拟合更强,或者说深层模型比浅层模型的参数效率更高!Yoshua Bengio 曾在他的论文[11]中做过一个说明,一个用深度为k的模型表达的函数如果用深度为k-1的模型来表达,所需要的参数数目将成指数倍增长!
说到模型拟合能力,事实上已经有很多模型可以做到对任意连续函数做到任意精度的逼近! 一个著名的关于神经网络拟合能力的定理说:单隐层神经网络即可任意逼近闭集上的任意连续函数,只要隐层节点数量足够多[12]! 这个定理叫做 Universal approximation theorem,其严格的叙述如下:
定理 令\(\psi(\cdot)\)是不为常量、有界、单调递增的连续函数,\(I_m\)是m维单位立方体\([0,1]^m\). \(I_m\)上的连续函数空间记为\(C(I_m)\). 那么,给定任意正数\(\epsilon>0\)和任意函数\(f \in C(I_m)\),存在正整数N、实数\(v_i, b_i \in R\)和实向量\(w_i \in R^m, i=1,…,N\),使得下述函数
\[F(x) = \sum_{i=1}^N v_i \psi(w_i^T x + b_i)\]可以以精度\(\epsilon\)逼近\(f\),
\[|F(x) - f(x)| < \epsilon, \forall x\in I_m\]即函数F(x)在\(I_m\)中稠密!
这个定理表明单隐层神经网络就可以拟合任意连续函数了,那为什么还要搞神马深度学习呢?一个重要的原因就是我上面说的那个:虽然两者只要神经元足够多,都能表达任意连续函数,但是如果神经元受限的情况下,深层模型的表达能力比浅层模型高得多得多!
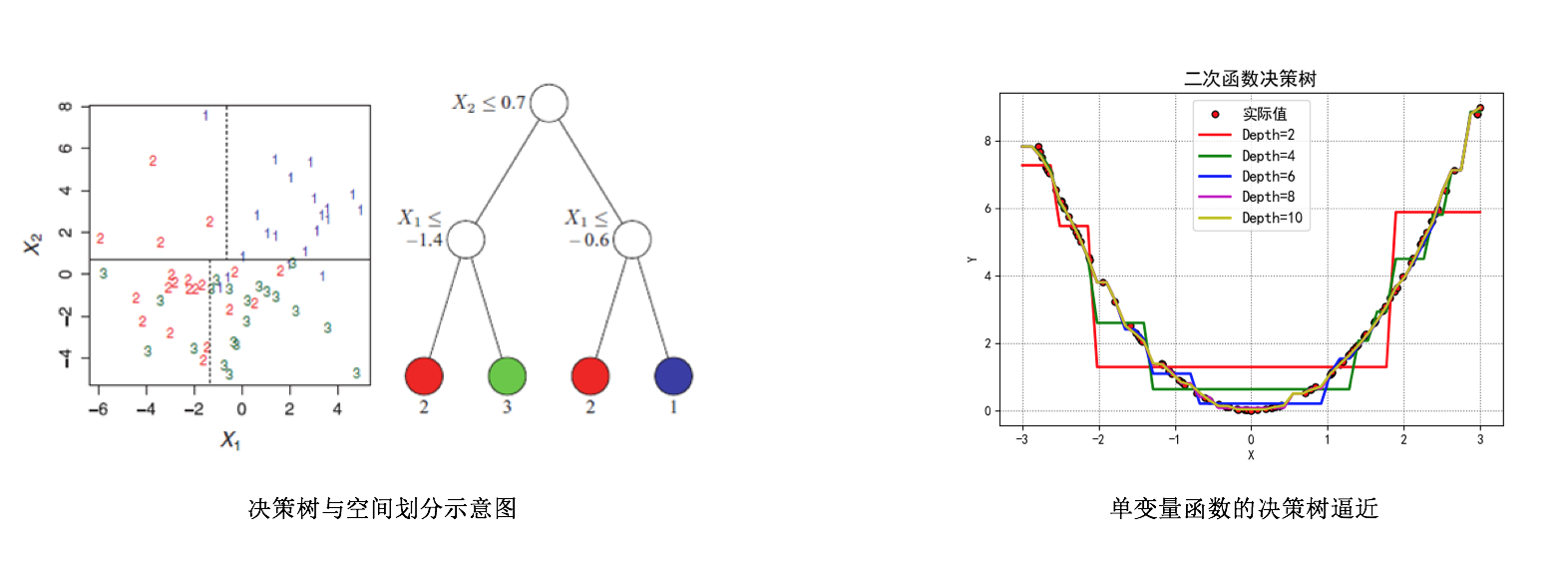
非线性模型中,除了神经网络之外,决策树也是很常用的模型,尤其是基于决策树的集成模型——随机森林(RF)和梯度提升树(GBDT)! 决策树本质上可以看做对输入特征向量构成的特征空间进行划分,将这个(连续或离散的)空间划分成很多个子区域,每个子区域对应树的一个叶子结点!每个子区域会对应一个预测值,在分类问题中预测一个类别或者概率,在回归问题中预测一个期望值!显然,只要这个划分划得足够细,那么定义在这个空间上的任意连续还是不连续的函数都可以以任意精度逼近!下图右边是逼近一个单变量二次函数的例子。
泛化与过拟合
前面说到,监督学习本质上就是在做函数拟合,而且有很多模型可以拟合任意连续函数! 那么,为什么不直接使用拟合能力很强的模型拟合数据就行了,还搞这么多复杂的模型结构,还研究个啥呢? 是不是做机器学习,把数据放入一个拟合能力很强的模型就可以了呢?
显然不是这样,其中一个很关键的问题就是模型的泛化能力与过拟合问题。 所谓过拟合是指在训练集上拟合得很好,比如拟合准确度很高,但是在没有看到过的样本(测试集)上预测效果很差! 因此可以通过交叉验证来发现模型的过拟合。例如下图中,虽然绿色的分类面可以完美地将两组数据分开,但是这个分类面对训练集非常敏感,在测试机上的效果很有可能不如黑色的分类面。 网上有人找到一张将过拟合非常有意思的图,过拟合可以将任何东西都看成模型想看成的东西,也许古代对星座的划分也算得上是一种过拟合吧!

过拟合的根本原因在于用有限的观测样本去估计整体, 对于参数化模型\(P(Y|X; \theta)\),通过极大似然估计来估计参数\(\theta\)。
\[\theta^* = \arg\max_{\theta} E_{(X, Y) \thicksim P(X, Y)} -\log P(Y|X; \theta) \\ \approx \arg\max_{\theta} \sum_i -\log P(y_i|x_i; \theta)\]如果观测样本十分有限,而模型的拟合能力又很强,那么最后一个等式的误差会非常大!
对于非参数模型,通常需要利用观测样本的一个子集来估计期望值等总体的统计量。 例如决策树模型,在每个叶子节点上,只用到满足该叶子节点对应规则的样本来估计期望值——正例的概率或者目标的期望值。 如果样本有限而决策树的叶子节点又特别多(模型复杂度高),那么落到一个叶子节点的样本数就非常有限,导致估计的误差很大!
根据偏差-方差分解,模型的预测误差可以分解为偏差和方差。 对给定的待预测样本\(x\),估计出来的预测函数\(\hat{f}\)会随着训练集的不同而改变,是一个随机变量。 假设实际的关系是\(y = f(x) + \epsilon\),\(\epsilon\)是噪声随机变量,所以\(y\)也是一个随机变量,但是\(f(x)\)是常数。
\[\begin{align*} E[(y - \hat{f}(x))^2] &= E[y^2 + \hat{f}^2 - 2y\hat{f}] \\ &=Var[y]+ Var[\hat{f}] +[Ey]^2 +[E\hat{f}]^2 - 2 f E\hat{f} \\ &= Var[y] + Var[\hat{f}] + (f - E\hat{f})^2 \\ &= \sigma^2 + Var[\hat{f}] + Bias[\hat{f}]^2 \end{align*}\]误差可以分为三项,第一项是该问题由于信息缺失等问题带来的固有误差,无法消除;第二项是\(\hat{f}\)因为训练集选取的不同所带来的统计涨落误差,称为方差;第三项是把所有可能的训练集都训练一遍,得到的函数预测值平均消除统计涨落后还无法消除的偏差!
模型的过拟合可以看做方差很大,对特定的训练集合误差很小而对其他训练集合误差很大,所以对某个固定的观测样本,模型预测的结果的波动受训练集的选择影响很大,也就是模型的方差很大。
机器学习之术
参考文献
- 国务院关于印发新一代人工智能发展规划的通知 http://www.gov.cn/zhengce/content/2017-07/20/content_5211996.htm
- 科技部召开新一代人工智能发展规划暨重大科技项目启动会 http://www.most.gov.cn/kjbgz/201711/t20171120_136303.htm
- Krizhevsky A, Sutskever I, Hinton G E. Imagenet classification with deep convolutional neural networks[C]//Advances in neural information processing systems. 2012: 1097-1105.
- Hinton G, Deng L, Yu D, et al. Deep neural networks for acoustic modeling in speech recognition: The shared views of four research groups[J]. IEEE Signal Processing Magazine, 2012, 29(6): 82-97.
- Rajkomar A, Oren E, Chen K, et al. Scalable and accurate deep learning for electronic health records[J]. arXiv preprint arXiv:1801.07860, 2018.
- https://www.kaggle.com/c/Higgs-boson
- Gao X, Duan L M. Efficient representation of quantum many-body states with deep neural networks[J]. arXiv preprint arXiv:1701.05039, 2017.
- Rupp M, Tkatchenko A, Müller K R, et al. Fast and accurate modeling of molecular atomization energies with machine learning[J]. Physical review letters, 2012, 108(5): 058301.
- Gilmer J, Schoenholz S S, Riley P F, et al. Neural message passing for quantum chemistry[J]. arXiv preprint arXiv:1704.01212, 2017.
- https://www.leiphone.com/news/201704/EHV2LSPT43FrGWJQ.html
- Bengio Y. Learning deep architectures for AI[J]. Foundations and trends® in Machine Learning, 2009, 2(1): 1-127.
- Hornik K. Approximation capabilities of multilayer feedforward networks[J]. Neural networks, 1991, 4(2): 251-257.