卷积网络的进化史
学习卷积网络有一段时间了,对卷积网络的演变过程中的一些基本思路有一个大致的理解, 于是总结出了这篇文章,一方面是加深自己的理解,一方面也希望对学习卷积网络的读者有所帮助。
综述
卷积网络是一种利用卷积提取序列或者空间数据局部或全局模式的一种网络, 其核心部分是所谓的卷积。事实上,卷积是一种特殊的数学运算,最早追溯到线性系统的建模。 线性是不变系统可以用一个冲击响应完备地描述,对于任何一个输入的信号,都可以将输出信号表达为输入信号与该系统 的单位冲击响应的卷积!从网络连接角度来看,卷积相当于局部连接并且在不同时间或者空间上共享连接权重。 一个卷积核事实上就是在提取某一种特殊的模式,事实上在图像处理系统中,很早就利用各种卷积核对图像进行处理, 例如高斯模糊核、拉普拉斯核、solber核等等。
最早将卷积操作引入神经网络中的工作应该是 LeCun 在1998年提出的 LeNet-5 [1],那里用到了现代卷积网络的两种基本操作: 卷积和池化pool,不同的是,Pooling用的是下采样的方式,而不是现代主流的 Max Pooling 或者 Avg Pooling。 但是,此后的10几年,由于计算能力的不足和标准数据的缺乏,卷积网络的效果一直不如浅层的网络。直到2012年,Hinton的学生 Alex Krizhevsky 利用一个8层的卷积网络,一举夺下著名的 ImageNet 比赛冠军,才让人们重新关注起神经网络[2]。可以说,Alex提出的AlexNet以及DBN在语音识别的重大突破[3],成为现在火热的深度学习爆发的导火索。因为,人们看到,在当时无法理解的所谓深度神经网络的帮助下,图像识别的准确率遥遥领先传统的方法10个百分点,让十年没啥突破的语音识别技术提升了9个百分点!于是,大家虽然不明白里面到底发生了什么,但是知道,这应该是未来最重要的方向没有之一。
自AlexNet后,一批批学者开始探索卷积网络的不同结构的影响,以及对卷积网络的可视化分析,让我们对卷积网络的认识越来越直观与深入。 其后的几个代表性工作如 ZFNet,VGGNet,GoogLeNet,Inception各种版本,ResNet etc[4-9,15]。探索了对卷积核的该进、连接方式的改进以及对卷积层的改进。使得模型能够越来越深,参数和计算复杂度越来越低,但是性能越来越好。理论上来讲,残差网络(ResNet)已经构造出一种结构,可以不断地增加网络的层数来提高模型的准确率,虽然会使得计算复杂度越来越高。它证实了我们可以很好地优化任意深度的网络。要知道,在那之前,在网络层数达到一定深度后,在增加反而会使得模型的效果下降!因此,残差网络将人们对深度的探索基本上下了一个定论,没有最深,只有更深,就看你资源够不够!另一方面,如何优化网络结构,使得较小的网络和较浅的网络也能做到极深网络的性能,但是计算复杂度和参数数目都控制在较小的范围内。这在移动端、嵌入式系统中的部署十分关键!在这方面,也有一些代表性工作,如 MobileNet [10],ShuffleNet [11]。未来,设计更高效的网络将是研究者的重要研究方向之一,其中高效应该包括用更少的参数、更少的计算资源、以及更少的标注样本!
基本组件
卷积网络一般都会包括两个基本组件:Convolution Layer, Pooling Layer. 可以说,是否包含这两个基本组件是区分卷积网络与其他类型的网络的重要标准。 一些新的网络结构通过使用大于1的stride,来实现空间维度的下采样降维,这种方法可以让网络结构中不显示地包含 Pooling 层, 可以理解为将 Pooling 的功能融合到卷积层当中。 另外的一些网络结构则将传统的卷积层的两个功能——空间卷积和特征混合分离出来,形成了1x1卷积层和Deepwise Separate Convolution层的两层结构来替代原有的单卷积层。
标准的卷积层(Convolution Layer)
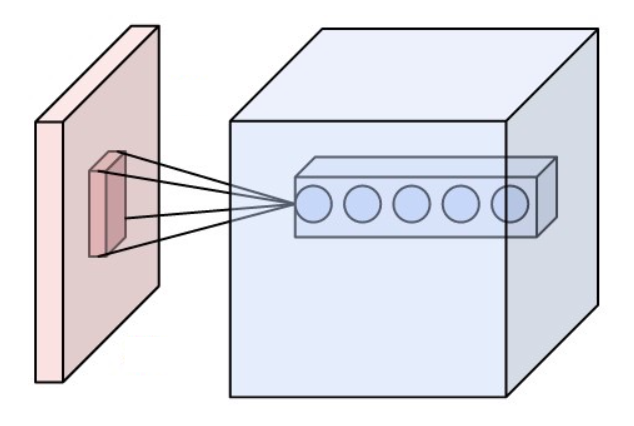
相比于全连接的神经网络,卷积网络的一大改进是采用局部连接并且在空间上共享权值——即卷积操作。 局部连接的对于图像、语音、词序列等具有局部相关性或具有局部模式的信号非常重要,局部连接可以很好地提取出这些局部的特征模式。 这种局部连接的想法受到了生物学里面的视觉系统结构的启发,视觉皮层的神经元就是局部接受信息的,这些神经元只响应某些特定区域的刺激。另一方面,自然图像固有的空间平稳统计特性使得在不同的区域使用相同的模板去抽取相同的特征,这就是权值共享。 下图是UFLDL上的一个简单的例子,形象地解释空间卷积操作的过程。
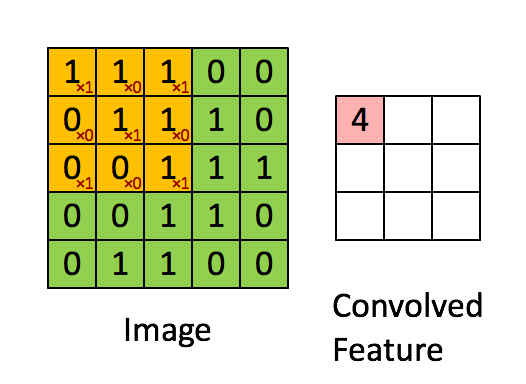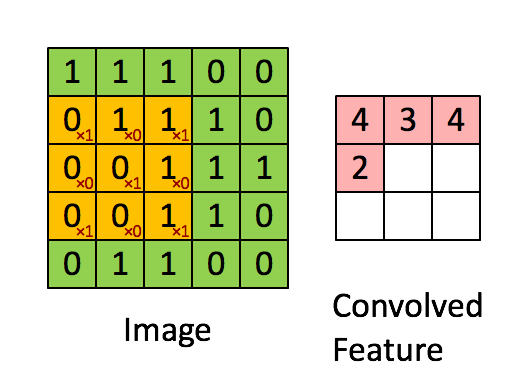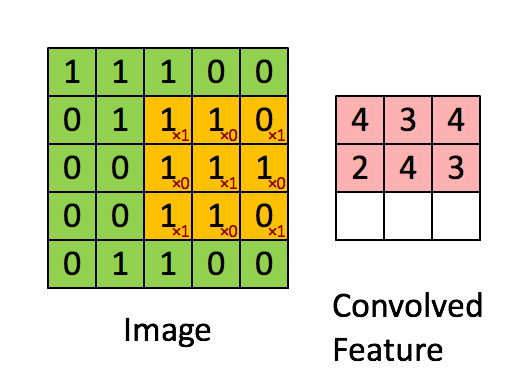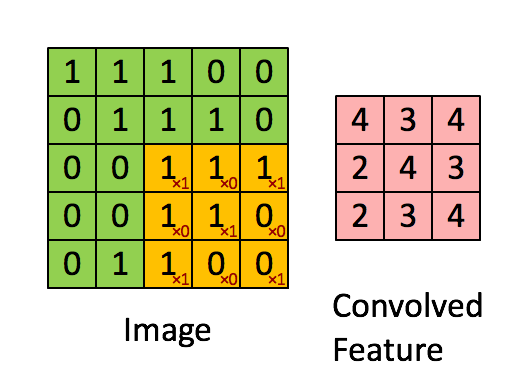
上图显示的是对单通道图片的单个卷积核的卷积过程,对于边界直接截断,所以卷积后的尺寸比原始图像尺寸要小一些。 一般地,对于多个通道的图像,如自然图像具有三个颜色通道,利用多个卷积得到的多个 feature map 构成的多通道, 卷积核除了要对空间维度进行卷积操作外,还会在通道维度进行全连接变换。假设输入图像用\(X_{ijf}\)表示, 其中i,j代表空间维度的下标,f代表通道;用\(w_{klf}\)代表一个卷积核,其中k,l代表空间维度,f代表通道, 那么经过卷积后输出的图像为
\[Y_{ij} = \sum_f \sum_l \sum_k X_{i-k, j-l, f} w_{k, l, f} .\]可以看到,多通道卷积操作具有两个功能,一是对空间维度进行卷积,而是混合输入图像的不同通道,这些通道可以是颜色通道,也可以是特征通道,因此相当与在特征维度进行全连接!后面可以看到,一些新的卷积层将这两个功能进行分离! 卷积层中有一种特殊的卷积核——1x1卷积,它的作用相当于只实现了特征维度的全连接操作,而没有空间维度的卷积操作,广泛地应用于特征降维、局部区域分类等应用当中,后面我们会经常碰到。
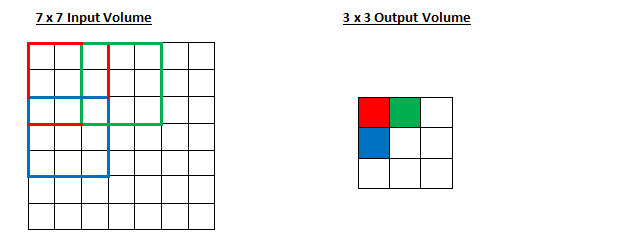
卷积操作还可以引入 stride,每次移动卷积核的步长可以大于1,可以减少输出的空间维度实现降维。 如下图所示的例子,它的stride=2,输出的空间维度在每个维度上都大约减少了一半。 另一个角度来看,它相当于将下采样的功能集中到卷积层当中,在卷积层中实现了Pooling操作。
在卷积网络中,卷积之后的结构往往会进行非线性操作后才作为该层的输出,\(f = \sigma(Y + b)\),\(\sigma\)是非线性激活函数,早期用得比较多的是 sigmoid,tanh激活函数,现在基本上都用 ReLU 激活函数及其变种,如 leaky ReLU[12],以及最近的研究提出自归一激活函数 SELU[13]。非线性激活函数的提供了整个网络的非线性变换特性。另一个提供非线性变换的地方是下面的池化层——Pooling。
每一个卷积核可以提取一个特定模式,所以一般的卷积层都会有多个卷积核,用于提取多个局部模式。
池化层(Pooling Layer)
池化操作是一种降维的方法,它将一个小区域通过下采样、平均或者区最大值等方式变成单个像素,实现降维。 池化操作除了降维外,还能在一定程度上实现局部平移不变性,即如果图片朝某个方向移动一小步,如果利用Max Pooling, 那么输出是不变的,这使得分类器具有一定的鲁棒性。因为这个原因,Max Pooling操作在卷积层中应用最为广泛。 下图是 Pooling 操作的示意图,来自 UFLDL[14]。而 Avarage Pooling 常用在全连接层的前面,将高层的卷积层输出的特征在空间维度平均,送入一个线性分类器当中。
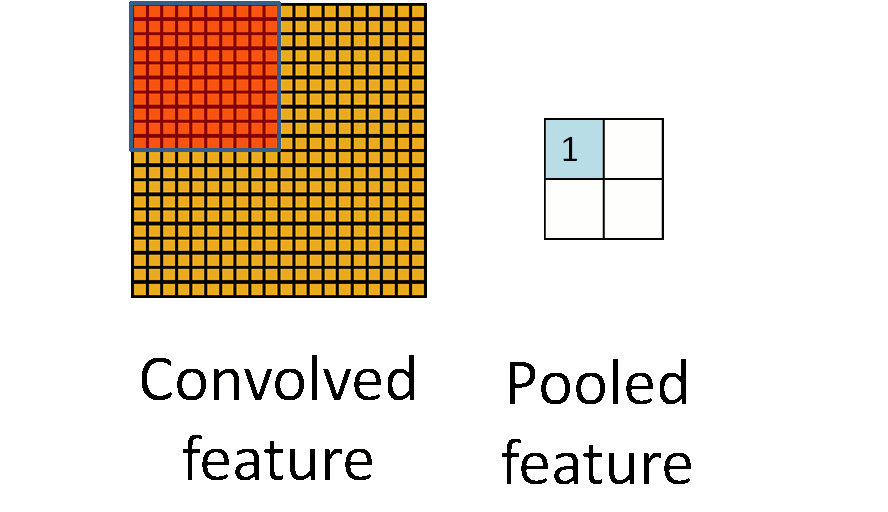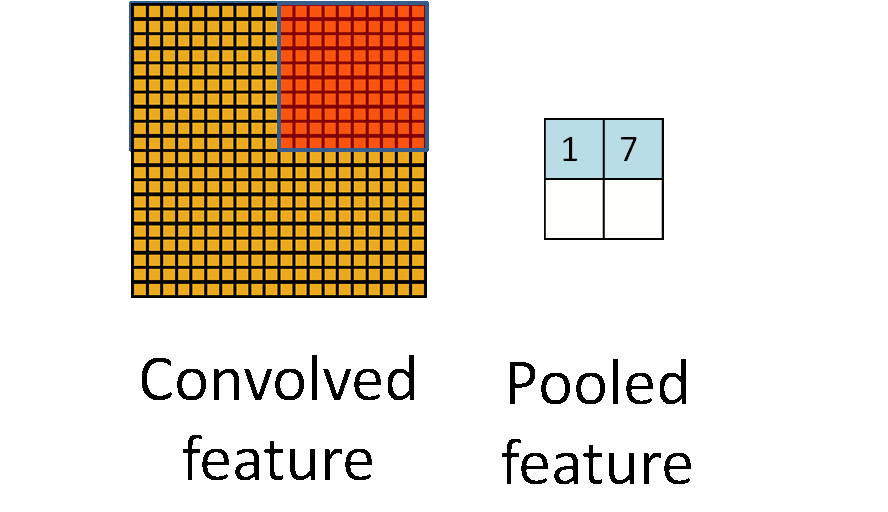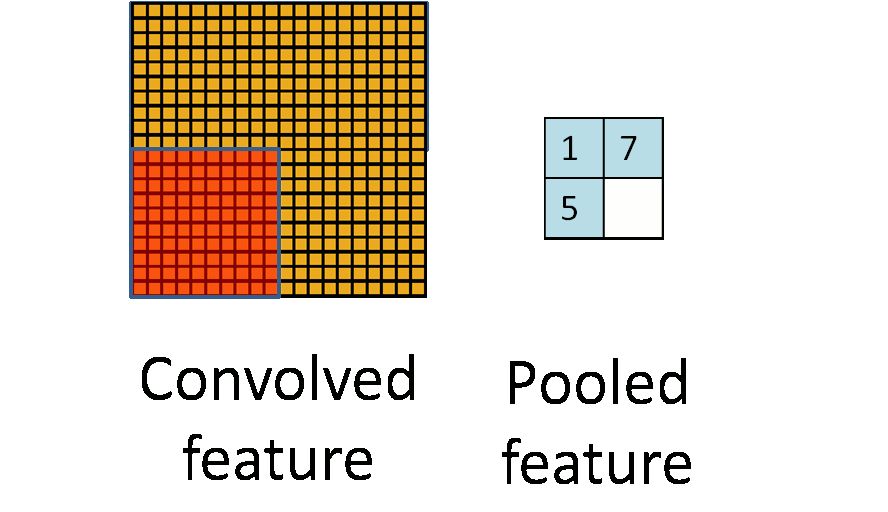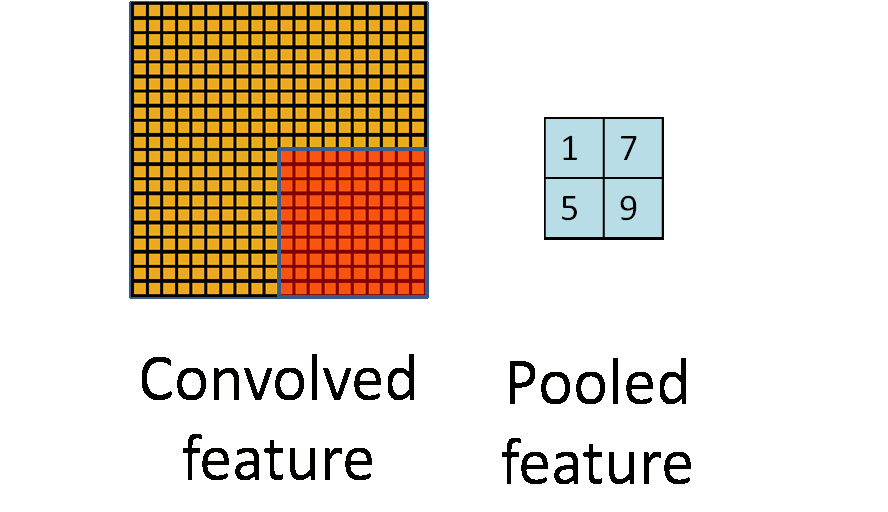
与卷积层类似,Pooling操作也可以引入stride,即跳过特定的距离进行 Pooling。上述示意图实际上是stride=Pooling的大小的特定情况。
卷积核分解
在早期,大家都用比较大的卷积核,如 LeNet-5 用的是5x5卷积核[1],AlexNet 用的是11x11, 5x5, 3x3卷积核[2]。 后来,大家发现,大的卷积核的效果不如用小的卷积核,为了达到相同的可视范围,可以通过增加卷积层,经过这样处理后, 实际上参数数目更少了,层数却变深了,导致的效果是,模型的分类效果反而变好了,因为用更少的参数,但是得到了更深和更多的非线性变换[15]。所以,后来大家都开始用3x3卷积核来构建卷积层。例如,用两层的3x3卷积可以达到和一层5x5卷积相同的可视范围。 如下图所示(图来自CS231N课程PPT),第二层单个神经元能覆盖到第一层的3x3的区域,第一层的每个神经元又可以覆盖到输入3x3的区域。 读者可以自己尝试画一下,可以看到两层3x3的卷积层后,使得第二层单个神经元能覆盖到输入层5x5的区域! 同理,三层3x3的卷积层, 最后一层的一个神经元可以看到的输入区域是7x7! 上述推导还是在stride=1的情况下的结论,如果使用stride=2的卷积,可视范围会更大! 假设输入图像的通道数为C,一个5x5的卷积核的参数数目为 \(25C^2\),这里假定输出通道数目也是C。 而两层3x3的卷积核的参数数目为 \(2\times 9C^2=18C^2\)。可以看到两层3x3卷积层在可是范围不减少的情况下, 参数减少了,意味着模型泛化能力更好。读者可以自己算一算7x7卷积核情况,参数数目从 \(49C^2\) 减少到 \(27C^2\), 参数数目减少接近一半!
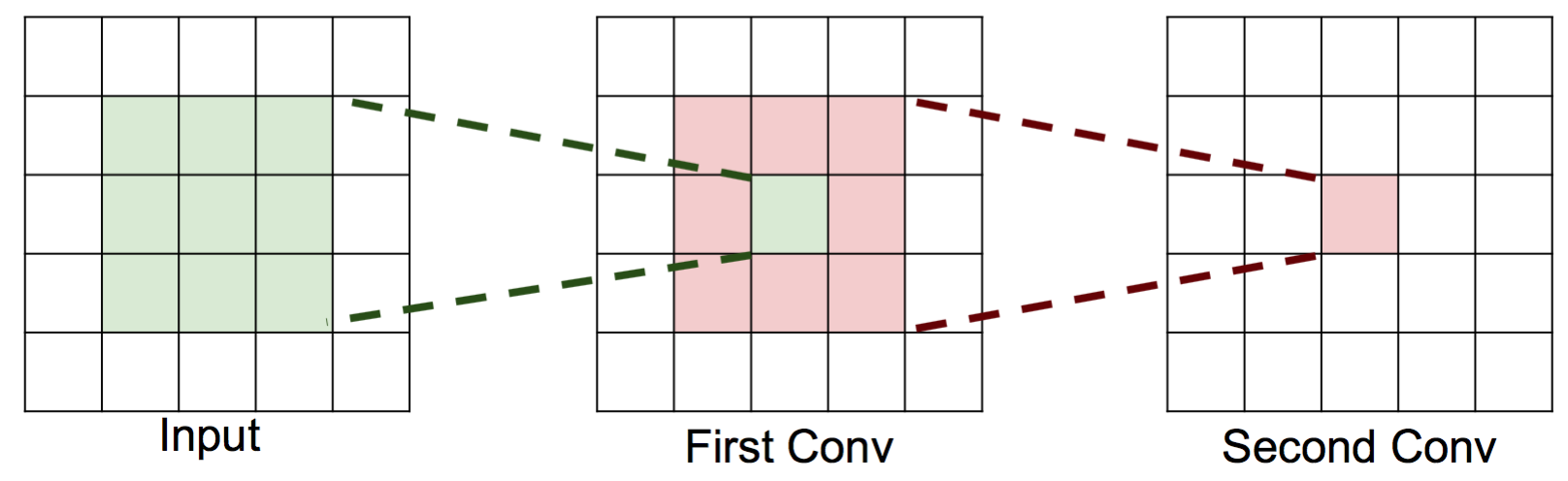
进一步,我们可以将3x3卷积核继续分解,将x和y两个方向的卷积分离开,形成两层卷积,分别是1x3卷积核3x1卷积核! 容易验证,这样的分解输出层的一个神经元的可视区域都是3x3!但是卷积核的参数数目从\(9C^2\)减少到\(3C^2\)!
从上面的分析,我们可以看到卷积核参数数目是通道数的平方,这是因为卷积核除了在空间卷积,在特征通道维度是全连接导致的。 基于这种分析,我们可以通过降维的方法进一步减少参数数目。降维的功能可以用1x1卷积核来做,连接方式是 1x1卷积C/2通道 - 3x3卷积C/2通道 - 1x1卷积C通道。参数数目为 \(C^2/2 + 9(C/2)^2 + C^2/2 = 3.25C^2 < 9C^2\),减少一半还要多! 这种结构被称作 Bottleneck 结构。
Inception结构
Inception 结构是由Google提来的,是 GoogLeNet[6]的关键结构。 他借鉴了 Network in Network[16],将单个卷积层变成一个小型神经网络,增加不同层次特征的组合。 解决了单个卷积层,同一个层的特征不能结合宏观(高层特征)和微观(低层特征)的特点。 而实现不同尺度的特征融合的方法是,利用不同的卷积核,然后将不同卷积核提取的特征concat到一起! 这种将不同尺度的特征融合的思想,在后面的 Densely Net [17]也可以看到。 在增加网络宽度的同时,为了不增加参数数目,可以利用1x1卷积核先进行降维,如下图所示。 从图中可以看到,这个 Inception 结构的输出,融合了4个尺度的特征。
Visual information should be processed at various scales and then aggregated. —- GoogLeNet[6]
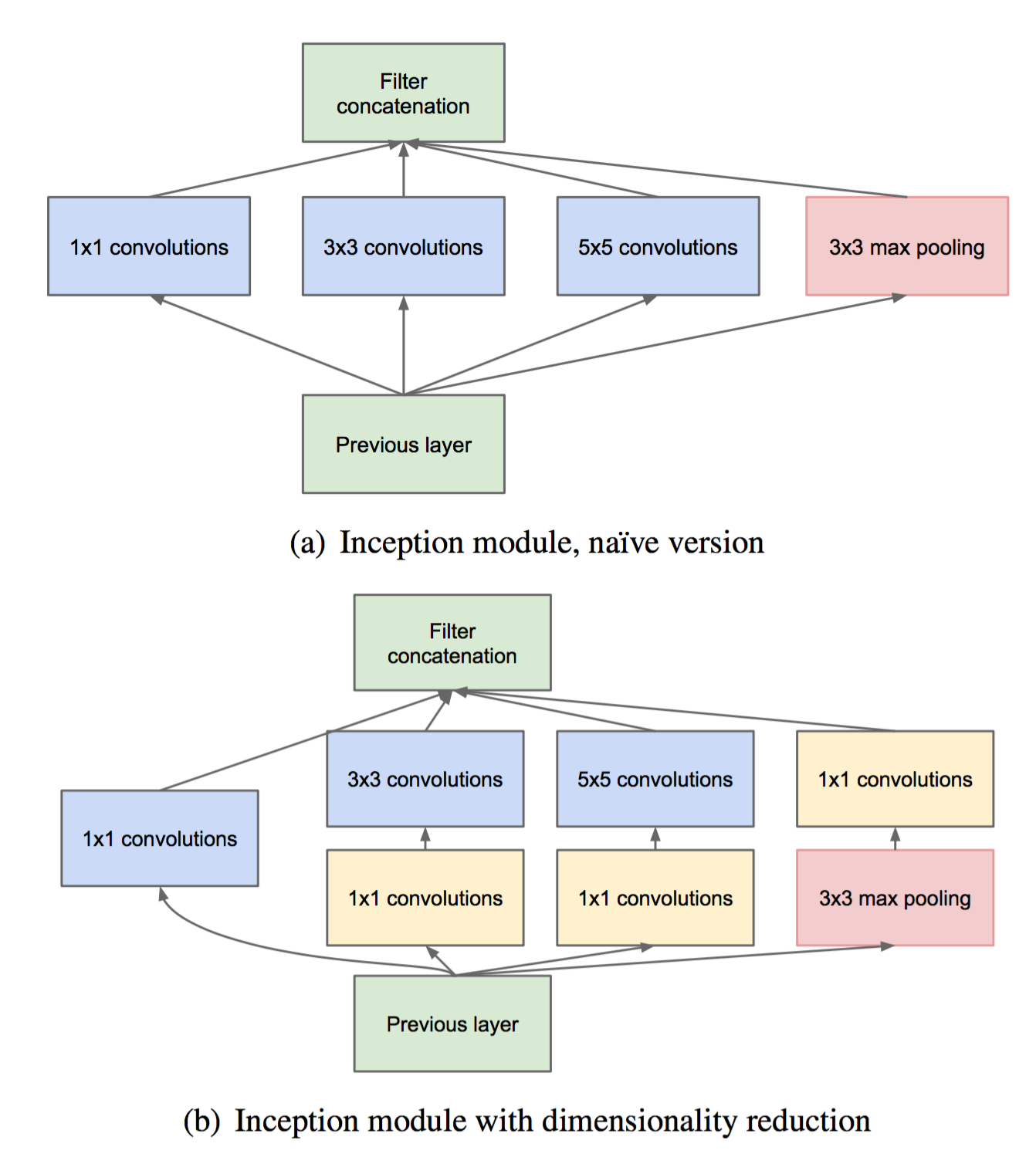
Depthwise Separable Convolution
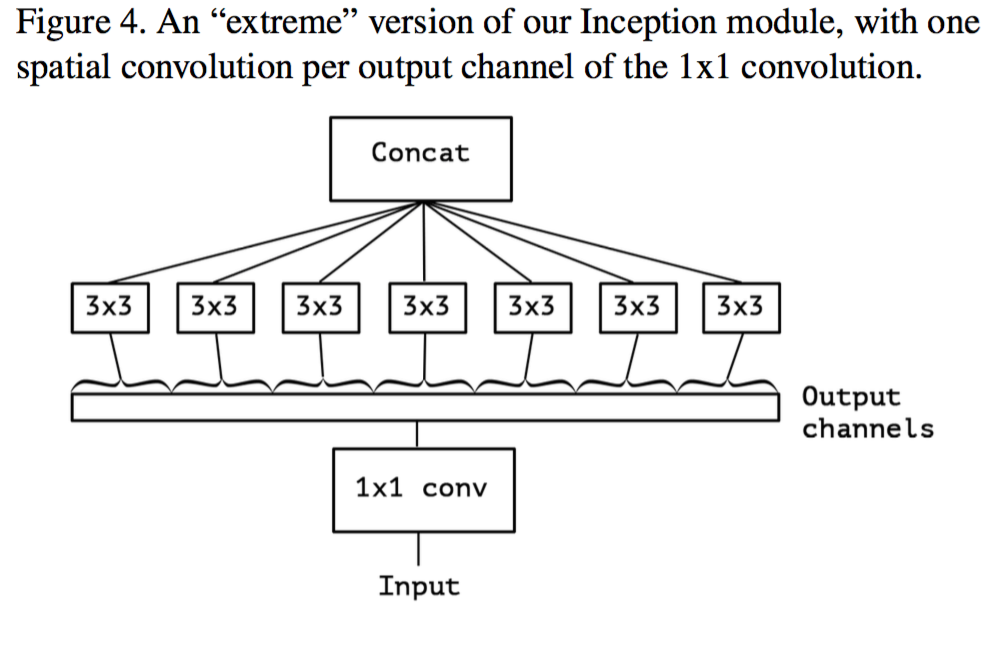
深度分离卷积(Depthwise Separable Convolution)由 Xception的作者 Chollet提出[9], 将卷积层的两个功能——空间卷积核特征通道全连接完全分解为两个部分。 作者假设,卷积层的这两个功能可以完全分解,并且不会降低卷积层的性能。 如下图所示,输入的 feature map 首先经过 1x1 卷积,将特征通道交叉, 然后在每一个输出的特征通道上(注意中间并没有非线性层),进行空间卷积操作。 这两个操作可以交换顺序,区别不大。 这样分解的好处是,参数数目少了很多。假设输入输出特征通道数目都是C, 3x3卷积核,并且同一个卷积核的权重在所有的通道数目是共享的。 那么传统的卷积层参数数目为 \(9C^2\),如果采用深度分离卷积,参数数目为 \(C^2 + 9C\)。 如果在两层中间使用 Bottleneck,即使用比C更小的通道数,可以进一步降低参数数目,此时的1x1卷积还起到降维的目的! Mobile Net也是基于深度分离卷积构建的,这种卷积结构可以极大地减少计算量,使得深度卷积网路这种复杂模型可以在移动端运行[10]!
the mapping of cross-channels correlations and spatial correlations in the feature maps of convolutional neural networks can be entirely decoupled. —- Xception.[9]
Group Convolution
分组卷积(Group Convolution)最早来自AlexNet[2],为了实现将同一个卷积层放在两个GPU上并行计算, Alex将每一个卷积层的特征通道分为两个部分,卷积层的全连接操作只在其中一部分操作,而不同特征通道之间的卷积计算互补干扰。 这种操作使得卷积层的计算并行化,提升了训练速度,但是不同特征通道之间不存在交叉会降低性能,为此,Alex在两个卷积层之间将特征进行交叉。实际上,这就是一个分组为2的分组卷积!Face++ 的研究者发展了这一方法,提出了分组卷积[11]。 实际上将上述的卷积层的功能之一——特征通道间的全连接进一步分解为多个组的分组全连接操作,实际上也就变成了部分连接了,也就进一步减少了计算量!例如,对于1x1卷积,通道为C,分组为g,那么一个卷积的计算复杂度为 \(C^2/g\),相比于原始卷积计算量减少了g倍,参数数目不变! 为了解决各组特征间的交叉,可以在每两层卷积层之间进行打散(shuffle)操作。

残差连接模式
很早以前,大家就知道可以通过增加深度的方法来减少神经网络的参数数目,因为实现相同的复杂度的函数,随着深度的增加,每层的神经元数目可以指数倍的减少!但是,深度增加后,难以训练,甚至会是的网络的性能变得比浅层网络效果更差。 但是,事实上,对于已有的一个浅层网络,如果新增的一层能够学到单位映射,即直接将输入的结果原样输出, 那么这个深的网络的性能应该和浅层网络性能一样!但是事实上,模型很难学到这个结果,何凯明大神创造性地为网络增加了一个跳跃连接,也有说是加飞线。设第l层输入向量为 \(x_l\),那么输出变为
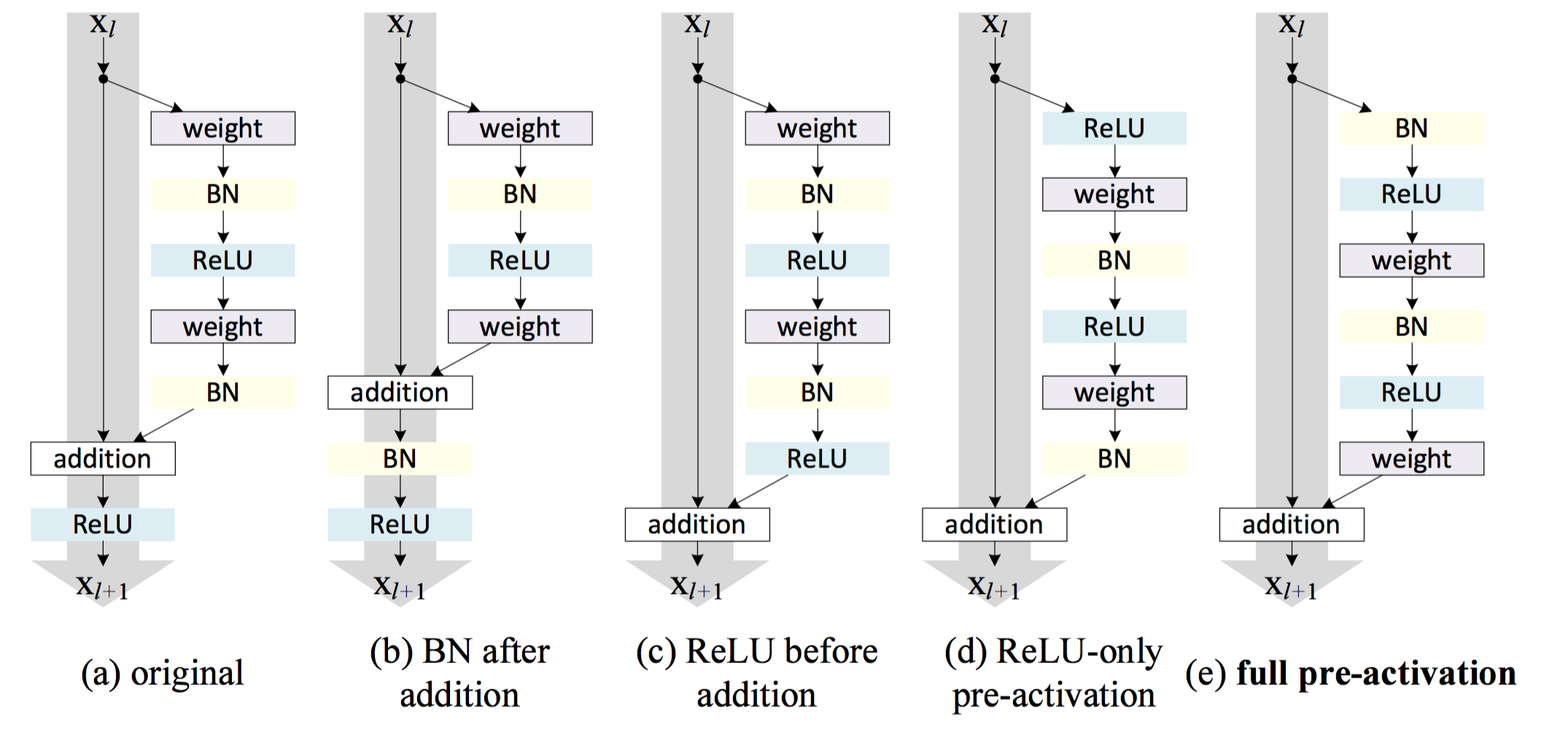
\[y_l = F(x_l; W_l) + x_l\]这里\(F\)代表参数为\(W\)的非线性变换,在卷积网络中通常是由Batch Normalize层、卷积层、非线性激活层构成。 可以看到,非线性变化实际上是在拟合残差,这也是为什么称作残差连接的原因。 在何凯明的第一版残差网络[8]中,输出向量\(y\)会再经过一个ReLU才灌入下一层,如下图(a)所示。这个结构让他将卷积层堆叠到了150层,取得了非常棒的结果,并一举夺下当年的ImageNet大赛的多项冠军,但是,当将这种结构继续堆叠至1000层时,效果又下降了。 经过分析发现,在短路通道的任何操作都会减少堆叠的深度[18]。
一般地,相邻两层的特征向量\(x_{l+1}, x_l\)之间的关系是
\[\begin{align} y_l &= F(x_l; W_l) + h(x_l) \\ x_{l+1} &= f(y_l) \end{align}\]只有当\(h(x)=f(x)=I(x)=x\),即都为单位映射时,效果最佳。原因在于,根据误差冒泡公式
\[\begin{align} \frac{\partial e}{\partial x_{l} } &= \frac{\partial e}{\partial x_{l+1} } f'(y_l)\left( h'(x_l) + \frac{\partial F}{\partial x_{l} } \right) \\ &= \frac{\partial e}{\partial x_{L} } \Pi_{k=l}^{L} f'(y_k) \left( h'(x_k) + \frac{\partial F(x_k, W_k)}{\partial x_{k} } \right) \end{align}\]假设\(\lambda_f \le |f'| \le \lambda_F, \lambda_h \le |h'| \le \lambda_H\), 而非线性网络部分的梯度范数因为正则项等原因,通常小于1,即\(|\frac{\partial F(x_k, W_k)}{\partial x_{k} }|<\lambda_c<1\). 如果放在短路链接上的两个变换\(f, g\)的梯度的下界都大于\(\lambda>1\),那么误差梯度
\[\frac{\partial e}{\partial x_{l} } \ge\frac{\partial e}{\partial x_{L} } \lambda^{2k}\]会随着k的增加,即网络深度的增加,指数增长。 反之,如果上界都小于\(\lambda <1\),那么梯度将随着k的增加,指数衰减! 因此,这种结构非常不稳定,存在梯度爆炸和消失(通常是消失)的问题,因而难以训练。 但是,当上述两个函数全为单位映射时,上式可以简化为
\[\frac{\partial e}{\partial x_{l} } = \frac{\partial e}{\partial x_{L} }\Pi_{k=l}^{L}\left( 1 + \frac{\partial F(x_k, W_k)}{\partial x_{k} } \right)\]从上式可以看到,右边那个连乘项展开有个常数项1,这表明梯度可以无变化地从高层流向底层,解决了梯度往底层流动的问题! 其他高阶项对应的梯度流经k层后的梯度,通常是随着层数增加而衰减。 试验也证实了这个结论,何凯明大神还专门写了一篇论文说明单位映射的重要性[18]! 经过这种改造后,连接模式变成了下图(c)-(d)的形式了。借助单位映射的力量,成功地刷出了1001层卷积神经网络!
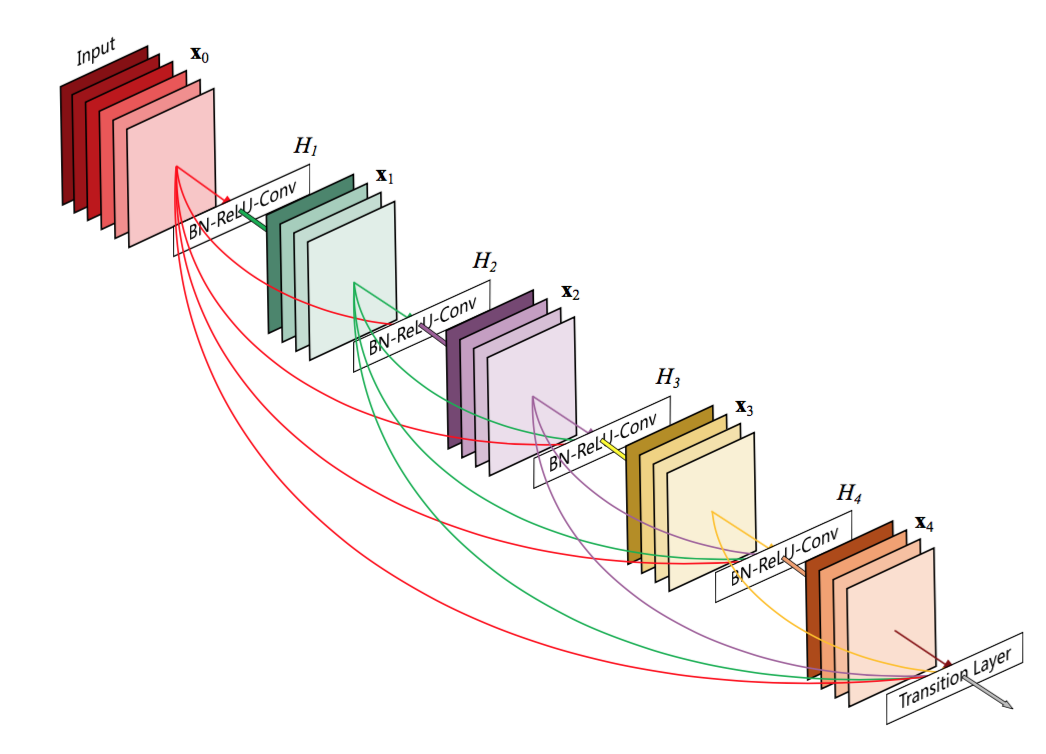
残差链接模式有一些变体,比如将比当前层低的所有层的输入都连接到当层,而不仅仅只把当前层的输入连接到输出, 这种连接模式由提出,被称作 Densely Connection[17]。 其中的思考是,不同层实际上表征的是不同尺度的特征,比如底层的是一些边缘,而高层的特征可能是一些物体形状模式。 因此,如果将不同尺度的表征都利用起来,就可以用更少的深度实现更好的模型效果。DenseNet的第l层的输出为
\[x_l = H_l([x_0, x_1, ..., x_{l-1}])\]\([x_0, x_1, ..., x_{l-1}]\)表示将前l层的输出都拼接到一起,作为第l层的输入,而残差链接只用到前一层!
后来,360的研究人员将ResNet和DenseNet融合起来,形成了所谓的双路径网络DPN!所谓的双路径,就是将ResNet路径和DenseNet路径的结果加起来![19]
总结与展望
本文总结了卷积网络相关的演化路程,总体思路是从浅层到深层,对卷积层做了各种优化,一方面改进结果减少参数数量,另一方面又增加非线性变换,增加不同尺度的特征。毕竟复杂如1000层的残差网络虽然效果好,但是计算量巨大,100层之后的层带来的收益太小,所以衍生出如DenseNet,DPN等结构。未来,一方面要减少计算量,另一方面又要提高模型的效果。
参考文献
- LeCun Y, Bottou L, Bengio Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278-2324. PDF
- Krizhevsky A, Sutskever I, Hinton G E. Imagenet classification with deep convolutional neural networks[C]//Advances in neural information processing systems. 2012: 1097-1105.
- Hinton G, Deng L, Yu D, et al. Deep neural networks for acoustic modeling in speech recognition: The shared views of four research groups[J]. IEEE Signal Processing Magazine, 2012, 29(6): 82-97.
- Zeiler M D, Fergus R. Visualizing and understanding convolutional networks[C]//European conference on computer vision. Springer, Cham, 2014: 818-833.
- Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition[J]. arXiv preprint arXiv:1409.1556, 2014.
- Szegedy C, Liu W, Jia Y, et al. Going deeper with convolutions[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2015: 1-9.
- Szegedy C, Ioffe S, Vanhoucke V, et al. Inception-v4, Inception-ResNet and the Impact of Residual Connections on Learning[C]//AAAI. 2017: 4278-4284.
- He K, Zhang X, Ren S, et al. Deep residual learning for image recognition[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2016: 770-778.
- Chollet F. Xception: Deep Learning with Depthwise Separable Convolutions[J]. arXiv preprint arXiv:1610.02357, 2016.
- Howard A G, Zhu M, Chen B, et al. Mobilenets: Efficient convolutional neural networks for mobile vision applications[J]. arXiv preprint arXiv:1704.04861, 2017.
- Zhang X, Zhou X, Lin M, et al. ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices[J]. arXiv preprint arXiv:1707.01083, 2017.
- Xu B, Wang N, Chen T, et al. Empirical evaluation of rectified activations in convolutional network[J]. arXiv preprint arXiv:1505.00853, 2015.
- Klambauer G, Unterthiner T, Mayr A, et al. Self-Normalizing Neural Networks[J]. arXiv preprint arXiv:1706.02515, 2017.
- Andrew Ng 的UFLDL教程
- Szegedy C, Vanhoucke V, Ioffe S, et al. Rethinking the inception architecture for computer vision[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2016: 2818-2826.
- Lin M, Chen Q, Yan S. Network in network[J]. arXiv preprint arXiv:1312.4400, 2013.
- Huang G, Liu Z, Weinberger K Q, et al. Densely connected convolutional networks[J]. arXiv preprint arXiv:1608.06993, 2016.
- He K, Zhang X, Ren S, et al. Identity mappings in deep residual networks[C]//European Conference on Computer Vision. Springer International Publishing, 2016: 630-645. MLA
- Chen Y, Li J, Xiao H, et al. Dual path networks[C]//Advances in Neural Information Processing Systems. 2017: 4470-4478.