AB测试与根号法则
AB测试是一种简单有效的试验方法,在上古时代,你很难判断某种营销策略是否比另外一种营销策略是否有更好的收益, 往往需要通过调查问卷的方式,而在互联网时代中,由于可以很容易获取到流量,这种实验变得非常简单。 在AI时代,线上某个算法的改进是否真得带来收益,也常常用AB测试进行检验。然而,看起来简单的AB测试,实际上并不简单。 本文针对工作中AB测试遇到的问题进行总结,并提供一些简单的理论探讨,希望对读者所有帮助。
什么是AB测试
设想,你是一个某个APP的产品,你认为蓝色的登陆按钮比现有版本的白色更加吸引用户,会增加用户转化为注册用户的转化率(当然实际中可能没有这么闲的PM,只是举个例子)。 为此,你让开发做了一个新版本,按钮是蓝色的。利用公司的AB测试系统,你很快就开始对新版本随机选取了10%的流量进行小流量测试。 经过一周的试验,你收集到如下数据
| 版本 | 注册页面用户数量 | 转化为注册用户数目 | 转化率 |
|---|---|---|---|
| 旧版本 | 1223223 | 122341 | 10.0% |
| 新版本 | 133423 | 15234 | 11.4% |
从转化率来看,新版本比旧版本高了1.4%,似乎效果很好,但是你也担心可能数据量不够,想多累积一段时间,再跟老板汇报。 那么,到底要累积多少数据才有说服力呢?实际上,对于上述数据仔细深究的话,会有这样几个问题:
- 数据是有统计波动的,所以通常要累积足够多的数据,1.4%的增量是真的有这么多的增量,还是数据波动带来的呢?
- 虽然在AB测试系统中,你配置了10%的小流量,但是整个试验中间经过了很多个系统,甚至AB测试系统本身可能存在BUG,这么多的系统串在一起,如何才能验证整个流程的AB测试是没有BUG,正常的呢?
虽然这只是我捏造的简单甚至可能不存在的场景,但是它基本上和目前所有用到AB测试的场景原理上没有太大差异。 对于第一个问题,直觉上是数据量越多,越有说服力,一般至少会测一周,消除星期的影响,但是一周的数据量是否足够往往根据前人的经验,难道没有一个客观的方法告诉我们要多少数据吗?对于第二个问题,很多时候都没怎么考虑过,对产品或者运营,往往都是十分信任AB测试系统,而一些做算法的工程师可能会考虑到这个问题。为了解决以上两个问题,下面先介绍一个非常简单的法则——根号法则。
根号法则
假设一个袋子中有非常多的球,球的颜色分为两种,白色和红色,其中红色占比为p=0.1。 如果我们从袋子中随机拿出一个球,观察他的颜色,然后放回;重复这个步骤N=100次,那么这N次中, 观察到红球的次数m可能有很多种情况,每种情况都有一定的概率,理论上m服从参数为(N, p)的二项分布, 我们把m的每一个取值作为X轴,对应的概率作为Y轴,就可以画出下面这个概率分布图。
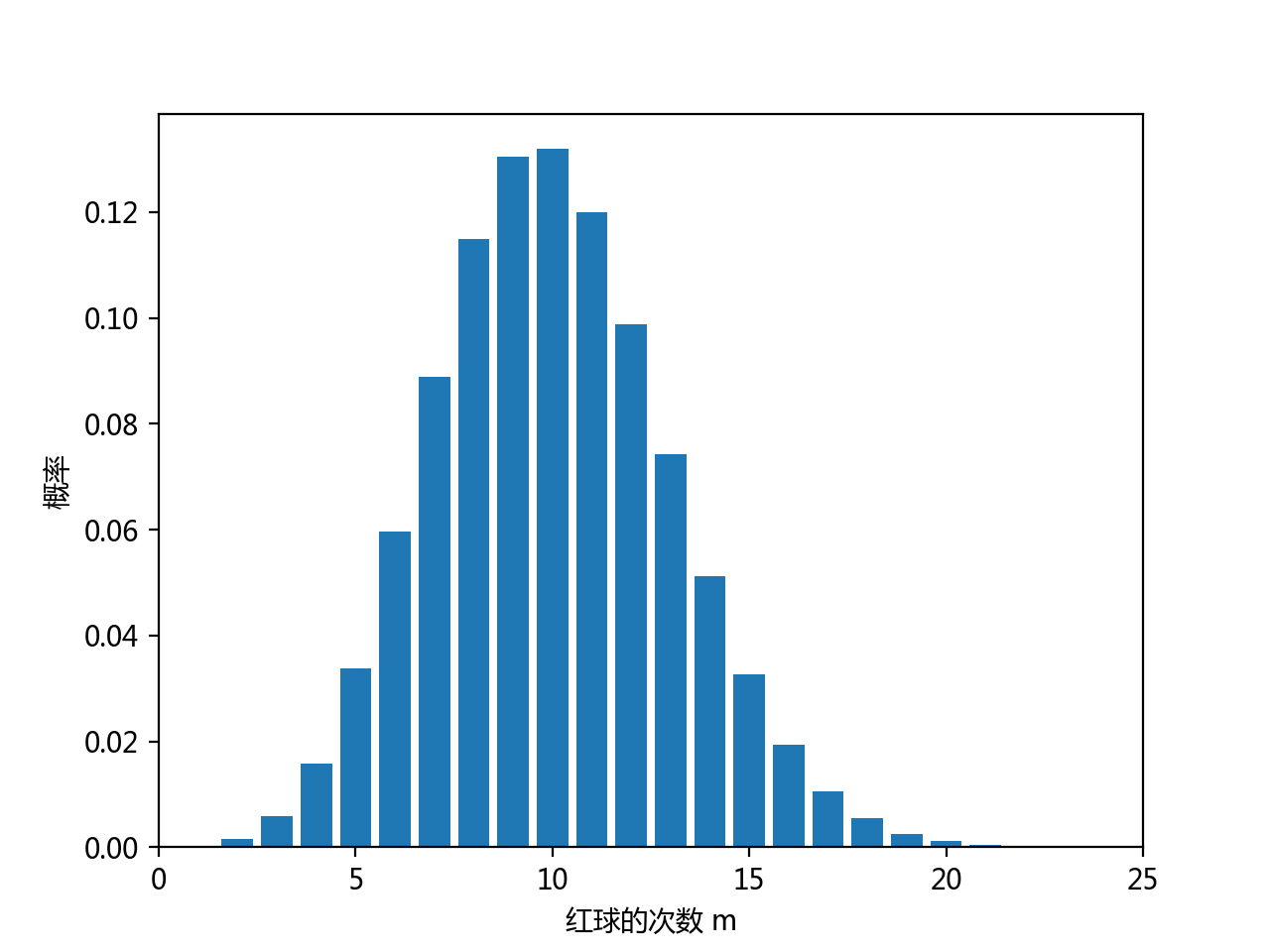
可以看到,出现20次以上的概率非常小了,出现10次的概率最大!平均下来,出现红色的次数等于 Np = 10次,也就是m的数学期望。 而某一次试验中,实际观察到红色的次数存在波动,数学上可以用方差/标准差 来描述这种波动。二项分布的方差很容易计算,它等于 \(Np(1-p) = 9\)。标准差是方差的开方,等于3,利用3个标准差原则,一次试验中m与期望值10之间的差异超过3个标准差(=9)的概率非常小,可以认为基本上不会发生,因此可以认为3个标准差就是m最大的可能波动。这在上面的分布图中也可以看到。超过3个标准差意味着m>=20或m=0,可见概率确实非常小。这表明我们可以用3个标准差作为m的波动的一个科学的度量。
如果从总体\(N\)个样本中以采样率\(p\)采样出来的样本数目为\(X\),在p远小于1时(比如本例),那么\(X\)的标准差可以等于 \(\sqrt{Np(1-p)} \approx \sqrt{Np} \approx \sqrt{X}\),也就是等于观察到样本数目开根号, 我把它称之为根号法则。利用根号法则可以快速计算出这种随机量的波动大小。下面我们将这个法则应用到前面的例子中,解答前面提出的2个难题!
根号法则解释AB测试中的两个问题
首先,我们来看一下数据中的1.4%是统计波动,还是确实有明显的增量(也叫具有统计显著性!)。 由于统计波动,两个方案中观察到的注册用户数目实际上也有波动,每一个用户可以看做一个球,转化的用户就是红球,没有转化的用户是白球, 那么转化的用户数目的标准差就是\(\sqrt{转化用户数目}\)。可以算出,在转化用户数目这个指标上,旧版本的标准差是350人,新版本的标准差是123人。如果用\(Z\)表示 新版本注册用户数目的增量,用\(Y\)表示 新版本注册用户数目,用\(X\)表示 旧版本注册用户数目,那么
\[Z = Y - X/9 = 1640人\]\(X\)和\(Y\)都可以看做从总体中以转化率采样出来的样本数目,所以利用根号法则可知它们的方差为
\[Var(X) \approx X, Var(Y) = \approx Y\]利用方差的可加性,增量\(Z\)的方差是这两项的方差之和,所以\(Z\)的标准差为
\[std(Z) = \sqrt{ Var(Y) + Var(X)/81 } \approx \sqrt{Y + X / 81 } = 129 人\]按照3个标准差法则,增量的波动最大不超过\(3std(Z)=387\)人,远小于观测到的增量1640人,所以观察到的增量十分显著,可以排除是统计波动带来的影响。
而且,我们可以计算出要具有统计显著性,转化率增量至少要超过 387/133423 = 0.3%。也就是说,只要转化率增量超过0.3%了,基本上可以确认不是统计波动,而是确实有增量。
此外,我们可以估计出转化率增量的不确定度。转化率增量等于\(Z\)除以新版本注册页面用户数量\(N\),所以转化率增量的不确定度为
\[\frac{\Delta Z}{N} = \frac{3 std(Z)}{N} = 0.3 \%\]所以,转化率增量的误差范围是 \(1.4 \pm 0.3 \%\) 。
接着,我们再来确认一下第二个问题,整个系统的AB测试是否有问题。我们可以把总的用户数目看做采样次数N,而新版本对应的用户数目是红球数目m,总的红球占比p=10%。因此,可以算出期望红球数目是 Np = 135665人,和实际观察到的偏差为 2242人,看其来也不多。按照根号法则,实际观察到的红球理论波动的标准差为 \(\sqrt{135665} = 368\) 人,也就是说实际偏差有6个标准差!远超过了最大3个标准差的范围,统计上可以认为单次试验中,这个事情不可能出现!!这表明,整套系统的AB测试流程出现了问题!!这个问题可能不是AB测试模块的问题,可能是展示的时候,数据表JOIN的时候等出现的问题!!具体原因就不得而知了,需要进一步排查系统问题。既然AB测试流程出了问题,那么前面得出的结论也不可靠!!现有的数据无法证明蓝色按钮比白色按钮好!由于AB测试出现了问题,导致实验数据全部白费了,这说明AB测试流程的正确性多么重要。
AB测试的校验-AA测试
上述对AB测试的数目进行简单的检验,检验与理论值之间的偏差是否超过了统计显著性范围,可以初步发现问题。 比如新老版本覆盖的用户量应该是1:9,通过上述方法很容易检测出是否满足这个关系,误差是否在统计显著性范围内。 但是,即使这种检验通过,并不能说明AB测试的数据就是可信的,因为数据量关系没问题,不代表流量是随机分的,可能新版本因为某种未知原因,天然就分到更多高转化流量,而分到更少低转化流量,总的流量又恰好满足1:9的关系。为了解决这个问题,可以采用进一步的AA测试进行校验。 所谓AA测试就是两份流量用得是同一个策略,比如上述案例,两份流量都用老版本,观察实验结果。
| 版本 | 注册页面用户数量 | 转化为注册用户数目 | 转化率 |
|---|---|---|---|
| 旧版本 | 1223223 | 122341 | 10.0% |
| 旧版本 | 134423 | 15234 | 11.3% |
假设上述数据就是AA测试的结果,流量比例可以验证,在误差范围内。但是,转化率上仍然有1.3%的差异。理论上,如果流量是均匀分的,那么转化率应该在统计误差的范围内,这个误差可以根据上述理论算出为0.3%。显然,这里转化率上的差异已经远远超过了统计误差,可以认为流量本身分布不均匀,AB测试系统存在问题,导致第二份流量天然就分到更多高转化流量!
根号法则用于采样误差估计
根号法则虽然简单,但是有很多有价值的用途。这里考虑一个采样问题,设想你想估计一个集合中满足某个规则的元素有多少个,如果这个集合非常大,一个一个验证非常耗资源,一个简单的方法是采样,比如采样p=1%的样本来验证。假设采样之后的集合中满足该规则的元素有m个,那么可以反推出原始集合中满足规则的元素大约在\(m/p = 100m\)个,问题是,这种采样估计的误差有多大呢?根号法则告诉我们误差不超过 \(3\sqrt{m}/p = 300 \sqrt{m}\)。因为m个元素可以看做从整体N个满足规则的元素中按照采样率p采样出来的,m的标准差为 \(\sqrt{Np} \approx \sqrt{m}\)。那么我们用 \(m/p\)来估计N,它的标准差当然就是 \(\sqrt{m} / p\)。因此,按照3个标准差准则,估计的误差不超过 \(3\sqrt{m} / p\)!
标记重捕法的误差分析
在生物学研究中,常用标记重捕法估计某个地区的动物(比如羚羊)数目,做法是先捕获N只羚羊,然后在他们身上做上标记,放回等到充分长时间后,重新捕捞M只,观察这M只羊中有多少只是有标记的,假设有K只有标记,那么总的羊数目可以估计有 Z = NM/K 只!那么这种方法的误差有多大呢?
从计算表达式可以看到,只有K是存在统计波动的,N和M都是常数。如果 \(K << M\),也就是每一只标记的样被第二次抓到的概率 \(<<\) 1。那么就可以利用根号法则得到,K的最大误差不超过 \(3\sqrt{K}\),所以,利用误差传递公式可得
\[\frac{\Delta Z}{Z} = \frac{\Delta K}{K} = \frac{3}{\sqrt{K}}\]所以,Z的估计误差为 \(\frac{3 Z}{\sqrt{K}}\).