关于
自编码模型常用做深度神经网络预训练。
历史
神经网络预训练方案
多层神经网络直接训练会因为局部最优问题,导致初值敏感,所以随机初始化效果不好。
可以采用局部无监督准则进行逐层初始化预训练,使得后续训练更大可能跳出局部最优。
- RBM:Hinton et al., 2006; Hinton and Salakhutdinov, 2006; Lee et al., 2008
- auto-encoder:Bengio et al., 2007; Ranzato et al., 2007
- semi-supervised embedding:Weston et al.,2008
- kernel PCA:Cho and Saul, 2010
RBM 和 自编码 模型函数形式很像,但是训练和解释都不同。一个很大不同是,确定性的自编码可以用实数值作为隐层的表达,
而随机的RBM采用二进制表达隐层。但是在实际上,应用在深度网络中的RBM还是用实数均值作为表达。
autoencoder 的重构误差可以看做 RBM 的 log-likelihood gradient 一种近似。
RBM 中的 Contrastive Divergence 更新。
如何构造一个好的表达!?采用无监督学习,学出输入中的重要模式!
好的特征表达: 交互信息 到 自编码
定义好的表达:对最终我们感兴趣的任务是有用的,相比不采用这种表达,它能够帮助系统更快地达到更高的性能!
A good representation is one that will yield a better performing classifier
实验表明,一个无监督准则的初始化,可以帮助分类任务得到明显地提升。
人类能够快速地学习新的东西一个重要的原因是已经获得了这个任务的一些先验知识。
学习一个输入$(X)$ 的表达$(Y)$,实际上是学习条件概率$(q(Y|X) = q(Y|X; \theta))$。$(\theta)$是要学习的参数。
一个基本要求是要尽可能保留输入的信息,在信息论里面可以表达为最大化交互信息 $(\mathbb{I}(X; Y))$: Linsker (1989)
独立成分分析(ICA):Bell and Sejnowski (1995)
$$
\arg \max_{\theta} \mathbb{I}(X; Y) = \arg \max_{\theta} - \mathbb{H}(X|Y) \\
= \arg \max_{\theta} \mathbb{E}_{q(X, Y)} [\log q(X|Y)]
$$
对于任意分布 $(p(X, Y))$,利用 KL 距离的性质可知:
$$
\mathbb{E}_{q(X, Y)} [\log p(X|Y)] \le - \mathbb{H}(X|Y)
$$
设这个分布通过参数$(\theta')$刻画,那么优化下面这个式子相当于优化条件熵的下界:
$$
\max_{\theta, \theta'} \mathbb{E}_{q(X, Y; \theta)} [\log p(X|Y; \theta')]
$$
当两个分布相同的时候,可以得到精确的交互信息。infomax ICA 中,特征映射为 $(Y = f_{\theta}(X))$。
那么$(q(X, Y;\theta) = q(X) \approx q^0(X))$,即用样本集的分布代替总体分布。优化问题变为:
$$
\max_{\theta, \theta'} \mathbb{E}_{q^0(X)} [\log p(X|Y=f_{\theta}(X); \theta')]
$$
UFLDL里面的独立成分分析:
找到一组基向量使得变换后的特征是稀疏的。
数据必须ZCA白化,标准正交基维数小于输入维度,是一组不完备基。
$$
\min || W x ||_1 \\
s. t. WW^T = I
$$
优化方法:梯度下降 + 每一步增加投影。
$$
W = W - \alpha \nabla_W || W x ||_1 \\
W = (WW^T)^{-1/2} W
$$
传统自编码
在传统 autoencoder(AE) 中,特征变换函数(Encoder)用sigmoid函数来近似:
$$
y = f_{\theta}(x) = s(Wx+b) \\
\theta = \{ W, b \}
$$
特征重构(Decoder)变换也用sigmoid函数
$$
z = g_{\theta'}(y) = s(W' y + b') \\
\theta' = \{ W', b' \}
$$
损失函数为重构误差:
$$
L(x, z) = \varpropto - \log p(x | z)
$$
- 对于实数值$(x \in \mathbb{R}^d, X|z \sim \mathcal{N}(z, \sigma^2 I)$,那么重构误差对应于均方误差$(L(x, z) = C(\sigma^2)||x-z||^2)$。
- 对于二进制变量 $(x \in \{ 0, 1 \}, X|z \sim \mathcal{B}(z) )$,那么重构误差对应于交叉熵损失函数。
常用的两种形式:纺射+sigmoid Encoder;纺射 Decoder + 均方误差, 纺射+sigmoid Decoder + 交叉熵损失函数
autoenoder 的训练最小化重构误差,即优化下列问题:
$$
\arg \min_{\theta, \theta'} \mathbb{E}_{q^0(X)} L(X, Z=g_{\theta'}(f_{\theta}(X)))
$$
等价于
$$
\arg \max_{\theta, \theta'} \mathbb{E}_{q^0(X)} \log(p(X| Y=f_{\theta}(X); \theta'))
$$
这表明,我们是在最大化X和Y的交互信息量的下界!
training an autoencoder to minimize reconstruction error amounts
to maximizing a lower bound on the mutual information between input X and learnt representation Y
但是,简单地保留原有信息是不够的!比如简单地将Y设置为X,但是这个并没什么卵用!
如果Y的维数不少于X,那么学一个单位映射就可以最大限度地保留X中的信息!
传统的autoencoder方法采用不完备的表达$(d' < d)$。
降维后的Y相当于X的有损压缩表达。
当采用纺射变换做编码和解码,而没有非线性变化,那么就是PCA!
但是引入非线性变化后,将能够学到不一样的特征表达!
The use of “tied weights” can also change the solution: forcing encoder and decoder matrices to
be symmetric and thus have the same scale can make it harder for the encoder to stay in the linear
regime of its nonlinearity without paying a high price in reconstruction error.
另外,也可以添加其他约束,而不是更低的维度。
例如通过添加稀疏约束,可以采用过完备的维度,即比输入更大的维度。
稀疏表达,稀疏编码:Olshausen and Field (1996) on sparse coding.
稀疏自编码(A sparse over-complete representations):sparse representations (Ranzato et al., 2007, 2008).
Denoise 准则
目标:还原部分腐蚀的输入,即降噪!Denoising
一个好的表达应该是能够鲁棒地表达腐蚀后的输入,可以帮助恢复任务!
输入加入噪声:高斯噪声(连续变量),椒盐噪声,马赛克噪声。
几何解释:
流形学习。
Variational autoencoders 论文导读
论文:Auto-Encoding Variational Bayes, Diederik P. Kingma, Max Welling, 2014
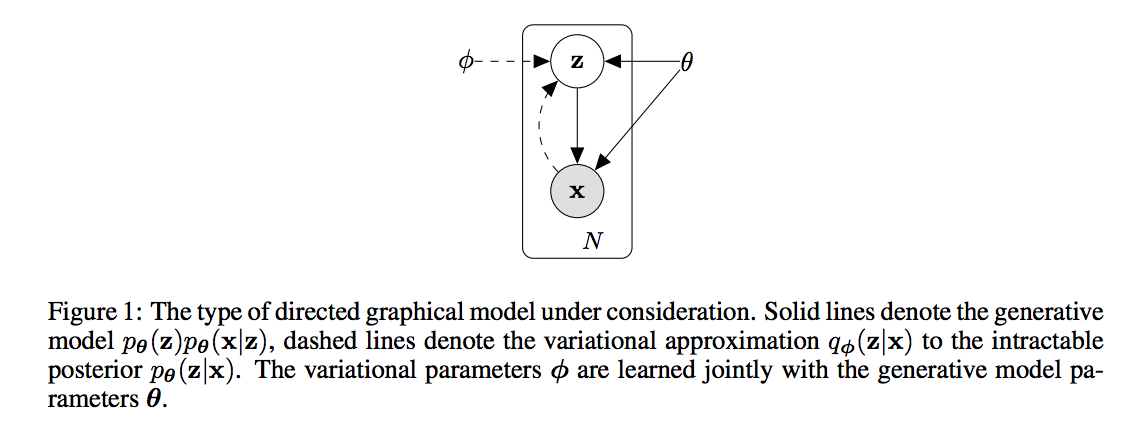
N个iid样本$(x^{(i)})$,连续或离散值。假定这些数据从一些随机过程产生!
- 从先验分布$(p_{\theta^* }(z))$产生隐变量$(z)$。
- 从条件概率$(p_{\theta^* }(x|z))$产生$(x)$。
假定先验分布和条件分布无限可微!
难点:
- 边际分布$(p(x))$需要计算一个积分,对于神经网络等复杂模型,难以求导!EM 算法失效;
- 大数据集,batch优化没有效率,需要随机梯度之类的优化
工作:
- 有效地近似地实现 ML 和 MAP估计参数$(\theta)$
- 给定x,推导z,有效的近似算法
- 有效的估计x的边际分布
建立识别模型$(q_{\phi}(z|x))$,近似$(p_{\theta}(z|x))$,编码角度来看,就是一个编码器!
而 $(p_{\theta}(x|z))$ 作为解码器!
变分界 variational bound
边际分布的对数似然函数为
$$
\log p(x^{(1)}, ..., x^{(N)}) = \sum_i \log p_{\theta} (x^{(i)})
$$
而其中每一项可以改写为
$$
\log p_{\theta} (x^{(i)}) = D_{KL}(q_{\phi}(z|x^{(i)}) || p_{\theta} (x^{(i)})) \\
+ \mathcal{L}(\theta, \phi; x^{(i)}) \\
\mathcal{L}(\theta, \phi; x^{(i)}) = \mathbb{E}_{q_{\phi(z|x)}}[-\log q_{\phi}(z|x) + \log p_{\theta}(x, z)] \\
= - D_{KL}(q_{\phi}(z|x^{(i)}) || p_{\theta}(z)) + \mathbb{E}_{q_{\phi(z|x^{(i)}}} \left[ \log p_{\theta}(x^{(i)} | z) \right]}
$$
对数似然函数第一项是近似误差,第二项是近似之后的似然函数,或者数据i的边际对数似然函数下界!
第二项可以写为一个KL距离和一个期望,前者可以通过解析积分计算,后者要采用近似估计!
而通常的 Monte Carlo 梯度估计在这个问题上方差太大,不适用与这里!
The SGVB estimator and AEVB algorithm
分布$(\tilde{z} \sim q_{\phi(z|x^{(i)}})$通过一个可微的变换$(g_{\phi}(\epsilon, x))$,
从一个noise变量$(\epsilon \sim p(\epsilon))$采样得到。
$$
\mathbb{E}_{q_{\phi}(z|x^{(i)})}[f(z)] \approx \frac{1}{L} \sum_{l=1}^L f(g_{\phi}(\epsilon^{(l)}, x^{(i)})), \\
\epsilon^{(l)} \sim p(\epsilon)
$$
mini-batch方法:
$$
\mathcal{L}(\theta, \phi; X) \approx \tilde{\mathcal{L}}^M(\theta, \phi; x^M) \\
= \frac{N}{M} \sum_{i=1}^M \tilde{\mathcal{L}}(\theta, \phi; x^{(i)})
$$
$({X^M})$ 是随机从全部数据集采样的M个数据。
auto-encoder角度:似然函数的第一项相当于正则,第二项是重构误差
例子:变分自编码
用多层感知器从输入学习到两个参数向量$(\mu, \sigma)$,
隐变量通过随机采样得到$(z \sim \mathcal{N}(z; \mu, \sigma))$。
解码器和编码器一样,从应变量z通过多层感知器学习到两个参数$(\mu', \sigma')$,
重构变量$(x' \sim \mathcal{N}(x'; \mu', \sigma'))$得到。
对于贝努利分布,参数只有一个均值。
Stacked What-Where Auto-encoders
论文导读:Stacked What-Where Auto-encoders, Junbo Zhao, Michael Mathieu, Ross Goroshin, Yann LeCun, ICLR 2016.
What: 就是polling后得到的max值,而where是最大值所在的位置信息,用来帮助解卷积器重构!
文章的方法将编码器学习和监督学习进行联合训练学习,作者认为(深度比较深时?)用自编码初始化的参数所携带的信息,
会在调优的时候丢失,导致预训练没啥乱用!而解决的方法就是进行联合训练。
此时,重构误差相当于一种正则!
目标函数为:
$$
L = L_{NLL} + \lambda_{L2rec} L_{L2rec} + \lambda_{L2M} L_{L2M}
$$
其中NLL代表监督学习的损失函数,负对数似然函数,对回归问题是L2损失,分类问题是交叉熵。
重构损失函数为L2损失函数。L2rec 代表输入和输出的重构样本的重构误差,L2M 代表中间编码器输入特征和解码器输出特征的重构误差。

实现监督学习,无监督学习,半监督学习的统一框架!
软最大值max和argmax
Ross Goroshin, Michael Mathieu, and Yann LeCun. Learning to linearize under uncertainty. arXiv preprint arXiv:1506.03011, 2015.

文章中,取$(\beta=100)$!
where的重要性

对比采用where信息做unpooling的重构结果和直接copy的upsampling的结果,可以看出where信息对重构输入至关重要!
想想也能想到啊!肯定重要啊!
what学习到的具有平移不变性!
结论

从论文中的结果来看,添加重构误差项还是挺重要的!
如果没有重构误差项,错误率会增加!
训练中也可以加入 droupout 正则化方法!
Reference
- Hinton, G. E. and Salakhutdinov, R. R. Reducing the dimensionality of data with neural networks. Science 2006.
- 2010, Pascal Vincent, Yoshua Bengio, Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion.
近期进展
- Richard Socher, Jeffrey Pennington, Eric H. Huang, Andrew Y. Ng, and Christopher D. Manning.
Semi-supervised recursive autoencoders for predicting sentiment distributions. In
EMNLP, 2011. - Variational autoencoders